Roots and exponents, also known as surds and indices, are fundamental concepts in GMAT Quant. Exponents represent repeated multiplication, while roots are the inverse operation, helping to undo exponentiation. These concepts often appear in various GMAT questions, from simple calculations to complex word problems, and understanding them is essential for success. Due coverage of roots and exponents should be an integral part of a thorough GMAT prep course. Let’s explore how these concepts are tested and how to approach them efficiently.
Roots and Exponents: Basic Principles
Roots and Exponents: Problems Requiring Rewriting Bases as a Common Prime Base (Example: If 252x = 125x – 3, x = ?)
When working through certain Quant problems on the GMAT, you’ll rely on a consistent and reliable method for handling exponents and roots. Begin by rewriting each expression with the same prime base. Convert roots into fractional exponents, combine like powers, and align the bases. Then, set the exponents equal to solve for the variable. If coefficients appear, either factor them out or express them with the same base. If that’s not possible, move them to the other side while keeping the bases matched. This approach simplifies the process, making it easier to solve the problems efficiently. The brief video below introduces this concept gently and illustrates how the GMAT may test it. Fully grasp this question type and its core concept. It will be useful as you tackle various problems in your GMAT drills, full-length GMAT mock tests, and, of course, the actual GMAT.
An Important Surds and Indices Question Type On GMAT
Roots and Exponents: Problems Requiring Cancelling Large Common Powers
[Example: If (251000 + 251001 + 251002 + 251003) ÷ (25999 + 251000 +251001 + 251002) = ?]
The GMAT often presents large powers in problems that may seem difficult at first. Instead of tackling the whole expression, look for terms that can be simplified. When high exponents appear in both the numerator and denominator, the largest power can usually be factored out and removed. What seems complex can often be reduced to something much simpler. The video below demonstrates this method and shows how it works in GMAT questions.
Another Important Surds And Indices Question Type On GMAT
GMAT-style Roots and Exponents Questions with Explanations
In this section, you will work through a set of GMAT-style Roots and Exponents questions, each with a clear, step-by-step explanation. Take your time with each question and apply the strategies you’ve learned for solving these types of problems. Focus on using the correct method rather than just getting the answer. After each question, use the explanation toggle to review the correct answer and understand the reasoning behind it.
GMAT Roots and Exponents: Practice Question 1
Written Explanation
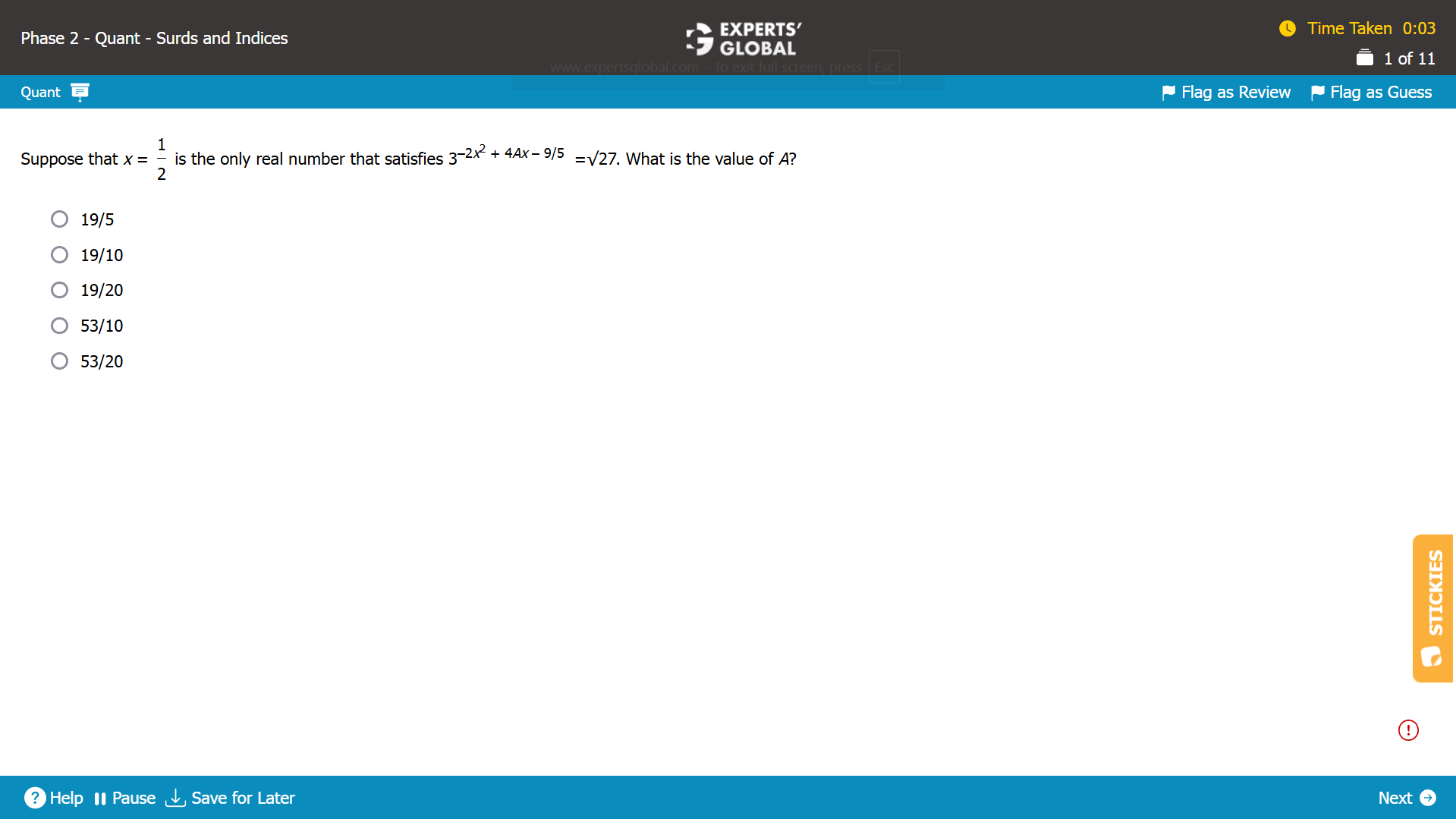
(10 – 6a)5 = –1
Taking the fifth root on both sides…
(10 – 6a) = –1
10 + 1 = 6a
a = 11/6
E is the correct answer choice.
GMAT Roots and Exponents: Practice Question 2
3–2x2 + 4Ax – 9/5 =√27
Substituting x = 1 / 2 in the above equation, we get,
3 –1/2 + 2A – 9/5 =√27
3 –1/2+ 2A – 9/5 = 3 3/2
Equating the powers on both sides, we get,
–1 / 2 + 2A – 9 / 5 = 3 / 2
Solving for A, we get,
A = 19 / 10
B is the correct answer choice.
GMAT Roots and Exponents: Practice Question 3
Written Explanation
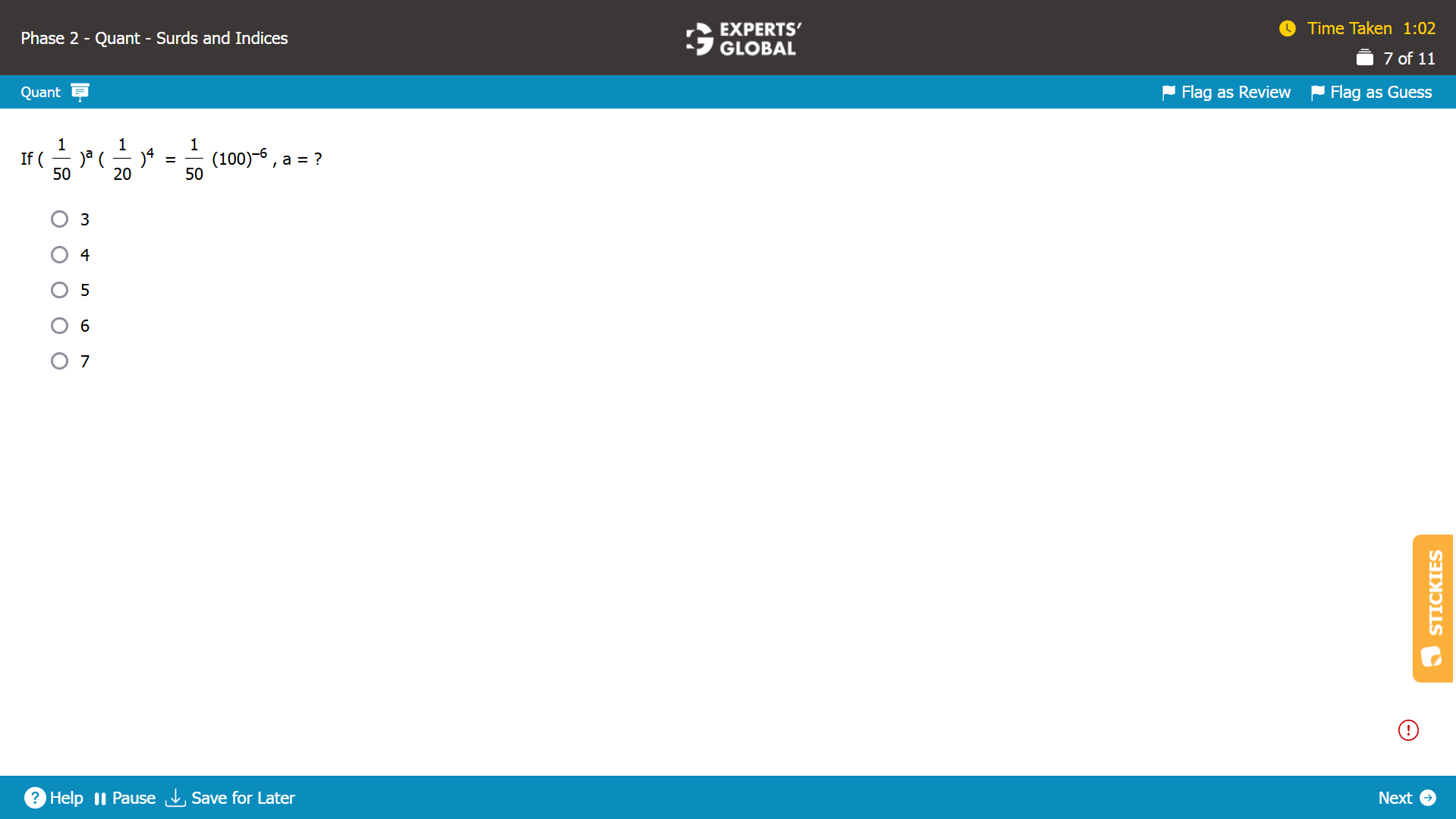
(1 / 50)a X (1 / 20 )4 = (1 / 50) X (100)–6 … (Equation I)
Let’s express all terms in prime numbers 2 and 5.
(1 / 50)a = (1/ 2 X 52)a = 2 (–a) X 5(–2a)
(1 / 20 )4 = ((1 / 22 X 5 )4 ) = 2–8 X 5–4
(1 / 50) = 1/ 2 X 52 = 2–1 X 5–2
(100)–6 = (22 X 52)–6 = 2 –12 X 5–12
Substituting in Equation I…
[2 (–a) X 5(–2a)] X [2–8 X 5–4] = [2–1 X 5–2] X [2 –12 X 5–12]
2 (–a – 8) X 5 (–2a – 4) = 2–13 X 5–14
Equating the powers of 2…
– a – 8 = –13
a = 5
[Alternatively, equating the powers of 5…
– 2a – 4 = –14
a = 5]
C is the correct answer choice.
GMAT Roots and Exponents: Practice Question 4
Written Explanation
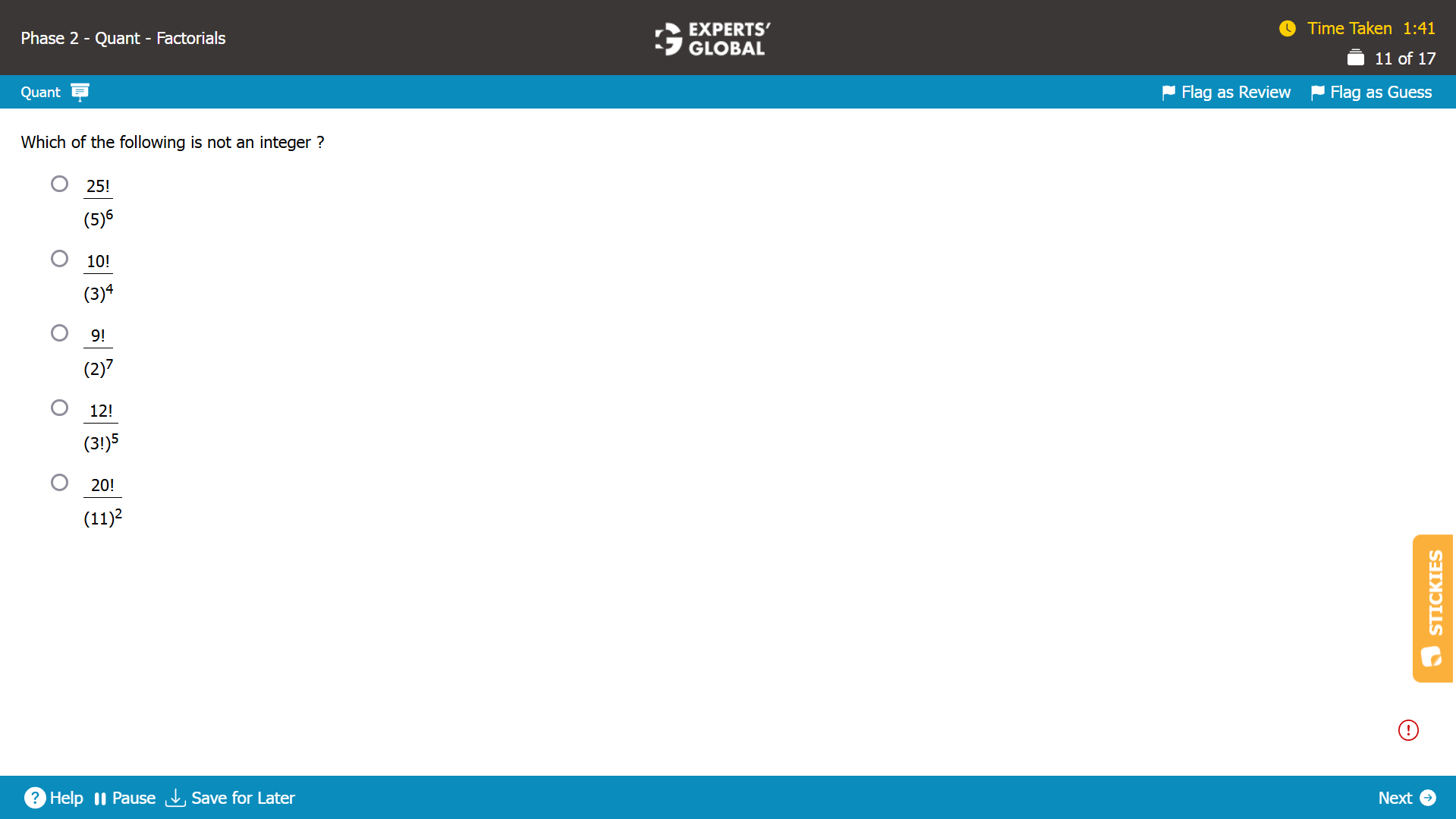
25! = 1 X 2 X 3.. X 24 X 25 = multiple of 5, 10, 15, 20, and 25.
Among all these multiples, there are…
Number of 5s in 5 = 1
Number of 5s in 10 = 1
Number of 5s in 15 = 1
Number of 5s in 20 = 1
Number of 5s in 25 = 2
Overall, there are 6 5s.
So, 25! / (5)6 will be an integer.
10! = 1 X 2 X 3.. X 9 X 10 = multiple of 3, 6, and 9.
Among all these multiples, there are…
Number of 3s in 3 = 1
Number of 3s in 6 = 1
Number of 3s in 9 = 2
Overall, there are 4 3s.
So, 10! / (3)4 will be an integer.
9! = 1 X 2 X 3.. X 8 X 9 = multiple of 2, 4, 6, and 8.
Among all these multiples, there are…
Number of 2s in 2 = 1
Number of 2s in 4 = 2
Number of 2s in 6 = 1
Number of 2s in 8 = 3
Overall, there are 7 2s.
So, 9! / (2)7 will be an integer.
12! = 1 X 2 X 3.. X 11 X 12 = multiple of 2, 4, 6, 8 ,10, and 12
Among all these multiples, there are…
Number of 2s in 2 = 1
Number of 2s in 4 = 2
Number of 2s in 6 = 1
Number of 2s in 8 = 3
Number of 2s in 10 = 1
Also, 12! = 1 X 2 X 3.. X 11 X 12 = multiple of 3, 6, 9, and 12
Number of 3s in 3 = 1
Number of 3s in 6 = 1
Number of 3s in 9 = 2
Number of 3s in 12 = 1
Overall, there are 10 2s and 5 3s.
12! / (2)5 will be an integer and 12! / (3)5 will be an integer. The product of these integers will also be an integer.
Overall, 12! / (3 X 2)5 = 12! / (3!)5 will be an integer.
20! = 1 X 2 X 3.. X 19 X 20 = multiple of 11.
Among all these multiples, there are…
Number of 11s in 11 = 1
Overall, there is only one 11.
So, 20! / (11)2 will NOT be an integer.
E is the correct answer choice.
GMAT Roots and Exponents: Practice Question 5
( 4 / 5 ) 1/10 = (0.8) 1/10
For any number between 0 and 1, taking the square root results in a larger number than the original.
As you continue to take higher-degree roots (cube root, fourth root, etc.), the result increases, progressively approaching 1.
Note: with higher-degree roots, the value would keep approaching but will always remain less than 1.
A is the correct answer choice.
GMAT Roots and Exponents: Practice Question 6
Written Explanation
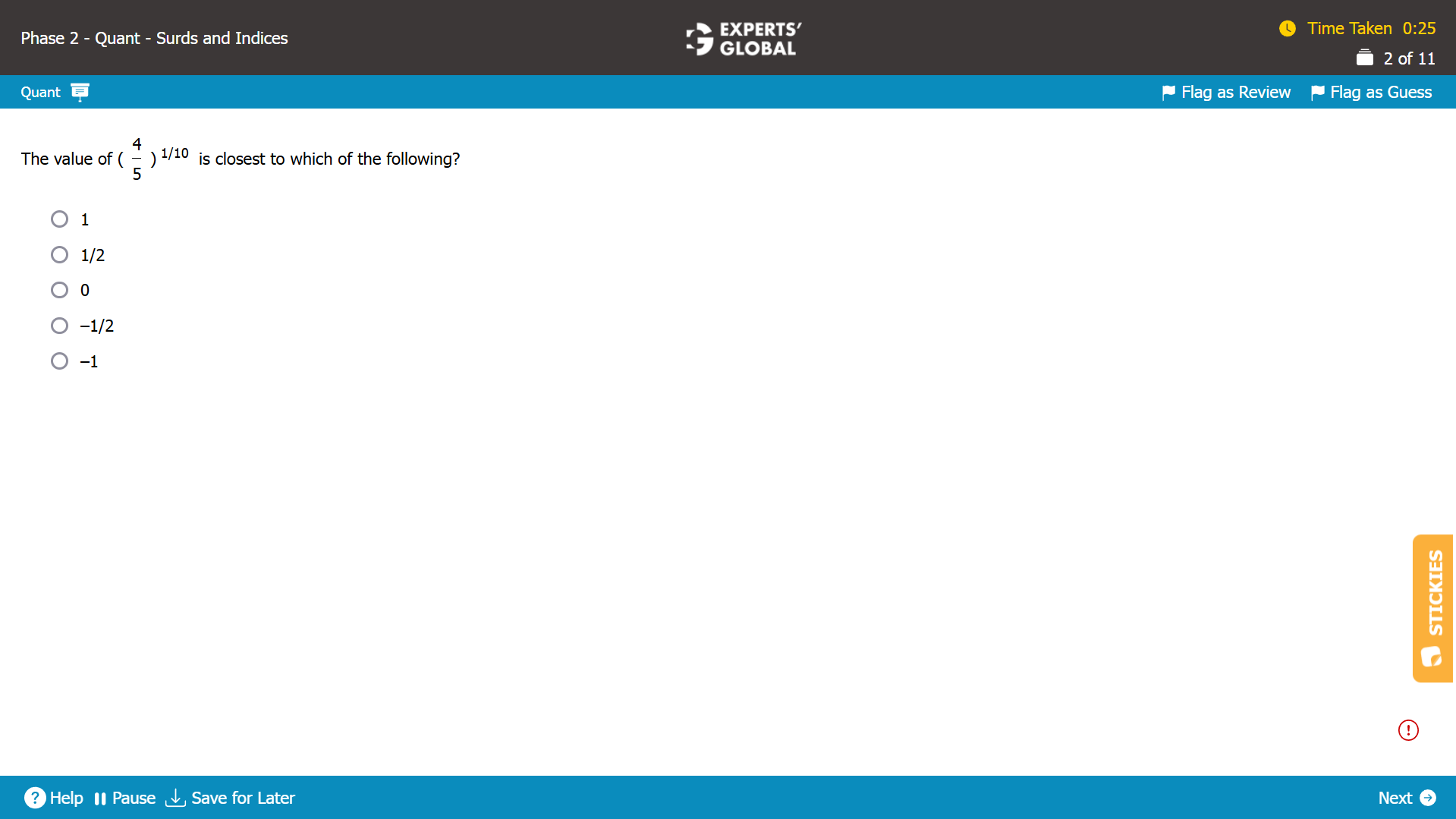
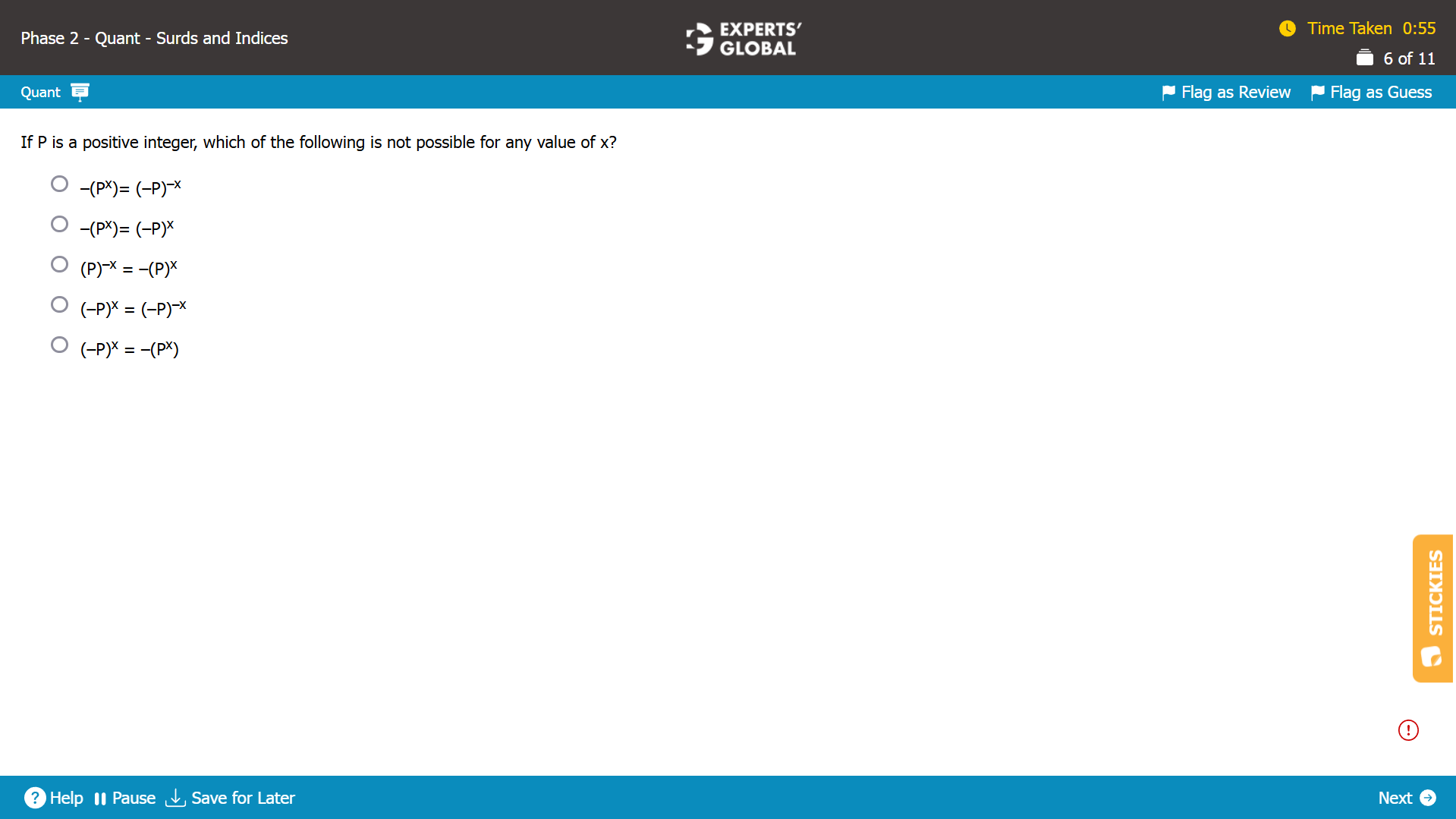
Let’s evaluate each answer choice.
Answer choice A
If P is a positive integer, any power of P will be positive; so, –(Px) will be negative for any value of x.
If P is a positive integer, (–P) will be negative; so, odd powers of (–P) will be negative; as a result, (–P)–x will be negative when x is odd.
For P = 1 and x = 3
–(Px) = –(13) = –1
and
(–P)–x = 1/(–P)x = 1/((–1)3) = –1
Therefore, –(Px) = (–P)–x is possible for some values of P and x.
Answer choice B
If P is a positive integer, any power of P will be positive; so, –(Px) will be negative for any value of x.
If P is a positive integer, (–P) will be negative; so, odd powers of (–P) will be negative; as a result, (–P)x will be negative when x is odd.
For P = 1 and x = 3
–(Px) = –(13) = –1
and
(–P)x = (–1)(3) = –1
–(Px) = (–P)x is possible for some values of P and x.
Answer choice C
If P is a positive integer, any power of P will be positive; so, (P–x) will be positive for any value of x.
If P is a positive integer, any power of P will be positive; so, (P)–x will be positive for any value of x and, as a result, –(P)–x will be negative for any value of x.
Therefore, –(Px) = (–P)x is NOT possible for any values of P and x.
Answer choice D
(–P)x = (–P)–x
Since the base on both sides of the equation is the same…
x = (–x)
x = 0
So, (–P)x = (–P)–x will be true for x= 0, regardless of the value of P.
(–P)x = (–P)–x is possible for some values of P and x.
Answer choice E
If P is a positive integer, (–P) will be negative; so, odd powers of (–P) will be negative; as a result, (–P)x will be negative when x is odd.
If P is a positive integer, any power of P will be positive; so, –(Px) will be negative for any value of x.
For P = 1 and x = 3
(–P)x = (–1)3 = –1
and
–(Px) = –(1)3 = –1
(–P)x = –(Px) is possible for some values of P and x.
C is the correct answer choice.
GMAT Roots and Exponents: Practice Question 7
3p5 = 96
p5 = 32
p = 2
7q = 32
q = 32 / 7
p / q = 2 / 32/7 = (2 × 7) / 32 = 7 / 16
B is the correct answer choice.
GMAT Roots and Exponents: Practice Question 8
n = (39719)(0.0018) = (3.9719 × 104) × (1.8 × 10–3) = (3.9719 × 1.8) × 10 ≈ (~4 × ~2) x 10 ≈ 80
B is the correct answer choice.
How and Where to Practice GMAT Roots and Exponents Problems
High-quality Roots and Exponents questions are also limited in number. Reliable sources include the official practice materials from GMAC and the Experts’ Global GMAT course. In the Experts’ Global GMAT online preparation course, every Roots and Exponents question is presented on a GMAT-like interface with all the real exam tools and features. You will work through over 250 Roots and Exponents questions in quizzes and take 15 full-length GMAT mock tests, each featuring a mix of Roots and Exponents questions in the same distribution as the actual GMAT.
All the best!
