Remainder problems on the GMAT are a key component of the Quantitative section, testing your ability to determine remainders when dividing numbers. These problems often appear on the GMAT, where you are asked to work with the given expressions and conditions to find the correct remainder in different scenarios. Mastering the concept of remainders is essential for success on the GMAT, and thorough preparation in this area should be an integral part of any dependable GMAT preparation course. By understanding these problems, you will improve your ability to tackle similar questions efficiently and boost your confidence for the exam.
Divisibility Rules, Tests, and Shortcuts
Divisibility tests are useful tools that can help you particularly with remainders problems. The most common tests are for divisibility by 2, 3, 4, 5, 9, 10, 11, and the higher powers of 2 and 5. Among these, the divisibility test for 11 is particularly unique and interesting. Understanding these divisibility tests will allow you to quickly identify factors and simplify problems without doing extensive calculations. The following set of infographics will help you master these tests with real-time examples. Be sure to understand them well, as they will be useful across all stages of your GMAT prep – whether in drills, sectional tests, GMAT full length mocks, or the actual exam.
Finding the Remainder Using Divisibility Rules
Finding the Remainder of a Large Multiplication
(Example: Finding the remainder of 1762 x 2938 x 2729 x 4625 with 9)
As you dive into GMAT preparation, remainder problems provide a powerful opportunity to see how basic concepts can simplify complex equations. Forget about complex multiplication – by tracking remainders and combining them carefully, you save time, boost accuracy, and sharpen your logical thinking. Check out the video below for a quick, easy-to-understand breakdown of this approach and how it might appear on the GMAT.
Finding the Remainder of a Large Multiplication
Finding the Remainder of a Large Exponent
(Example: Finding the remainder of 3379 when divided by 13)
In the questions requiring the remainder of a large exponent, the goal is to quickly and accurately find the remainder of a large power. In your GMAT prep, you follow a simple method. Start by reducing the base by the divisor, then test small powers of this reduced base until you find one that leaves a remainder of +1 or −1. This exponent is your cycle length. Now, reduce the original exponent using this cycle, replacing the big power with 1 or −1. If you get −1, add the divisor to make the remainder positive. For any extra factors, just repeat the reduce and shrink steps. This approach keeps numbers manageable and eliminates the need for complex multiplication. Watch the video below for a straightforward explanation of this technique and how it shows up on the GMAT.
Finding the Remainder of a Large Exponent
Finding the Remainder When the Divisor Changes
(Example: Integer N leaves remainder 47 when divided by 72; what remainder will N leave when divided by 18?)
In your GMAT prep, a key habit is organizing numbers neatly and clearly. Remainder questions become much easier when you write a number as N = d × q + r and see how this format changes with different divisors. This article highlights a pattern the GMAT loves: you’re given that N leaves remainder r when divided by d, and your task is to find the remainder when N is divided by a factor or multiple of d. We’ll simplify the big expression, eliminate what doesn’t matter, and carefully track the smaller remainder, step by step. The goal here is clear thinking, not complicated math. Watch the video below for a simple explanation of this concept and see how the GMAT might test it.
Finding the Remainder When the Divisor Changes
GMAT-style Remainders Questions with Explanations
GMAT Remainders: Practice Question 1
Written Explanation
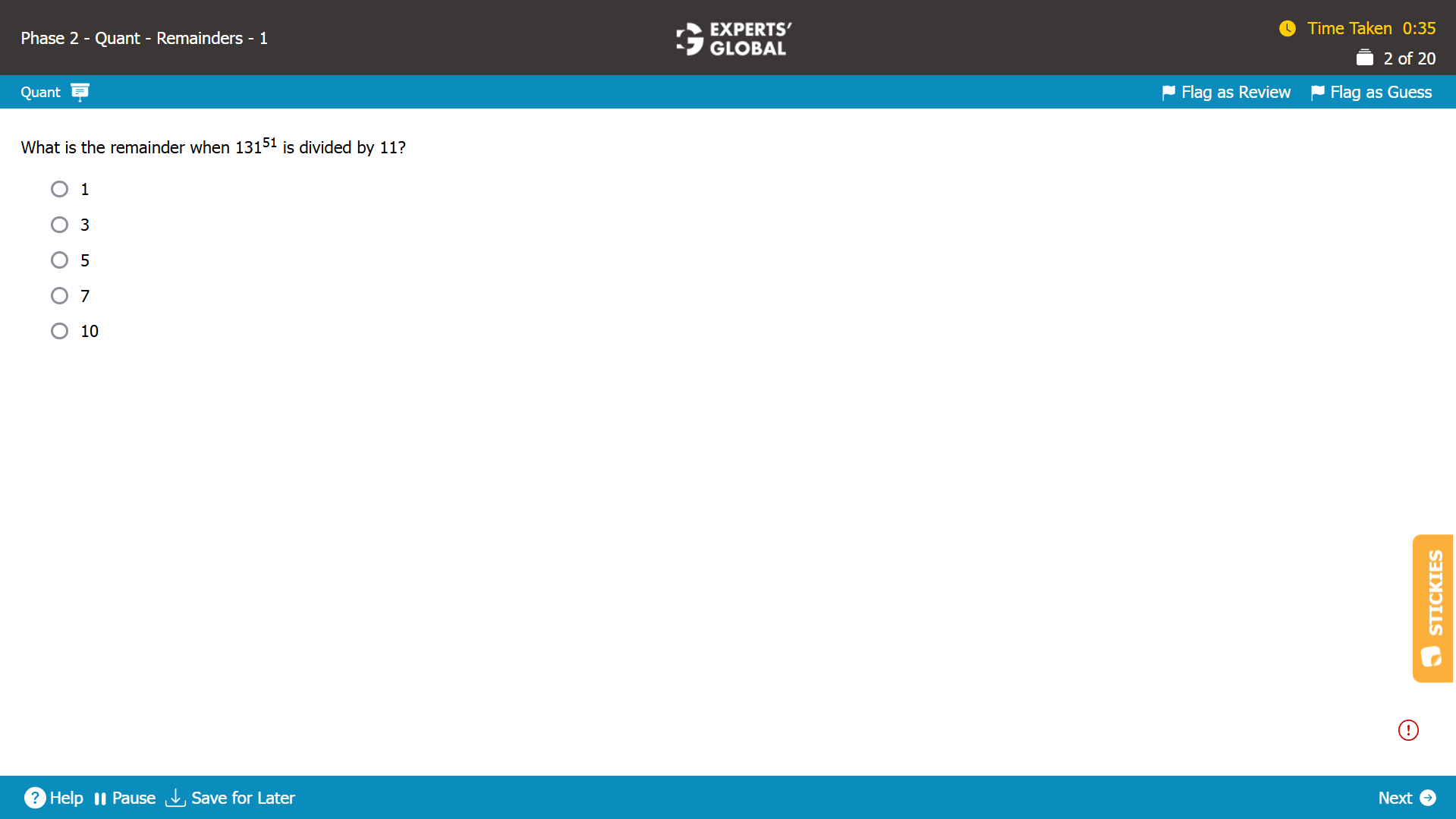
Remainder when 13151 is divided by 11 = Remainder when (131 X 131 X 131 …51 times) is divided by 11
= (Remainder when 131 is divided by 11)51
132 = 11 X 12
131 leaves a remainder of –1 when divided by 11.
So, remainder when 13151 is divided by 11 = (Remainder when 131 is divided by 11)51 = (–1)51 = –1.
A remainder of –1 when divided by 11 indicates the remainder of –1 + 11 = 10.
Remainder when 13151 is divided by 11 is 10.
E is the correct answer choice.
GMAT Remainders: Practice Question 2
Written Explanation
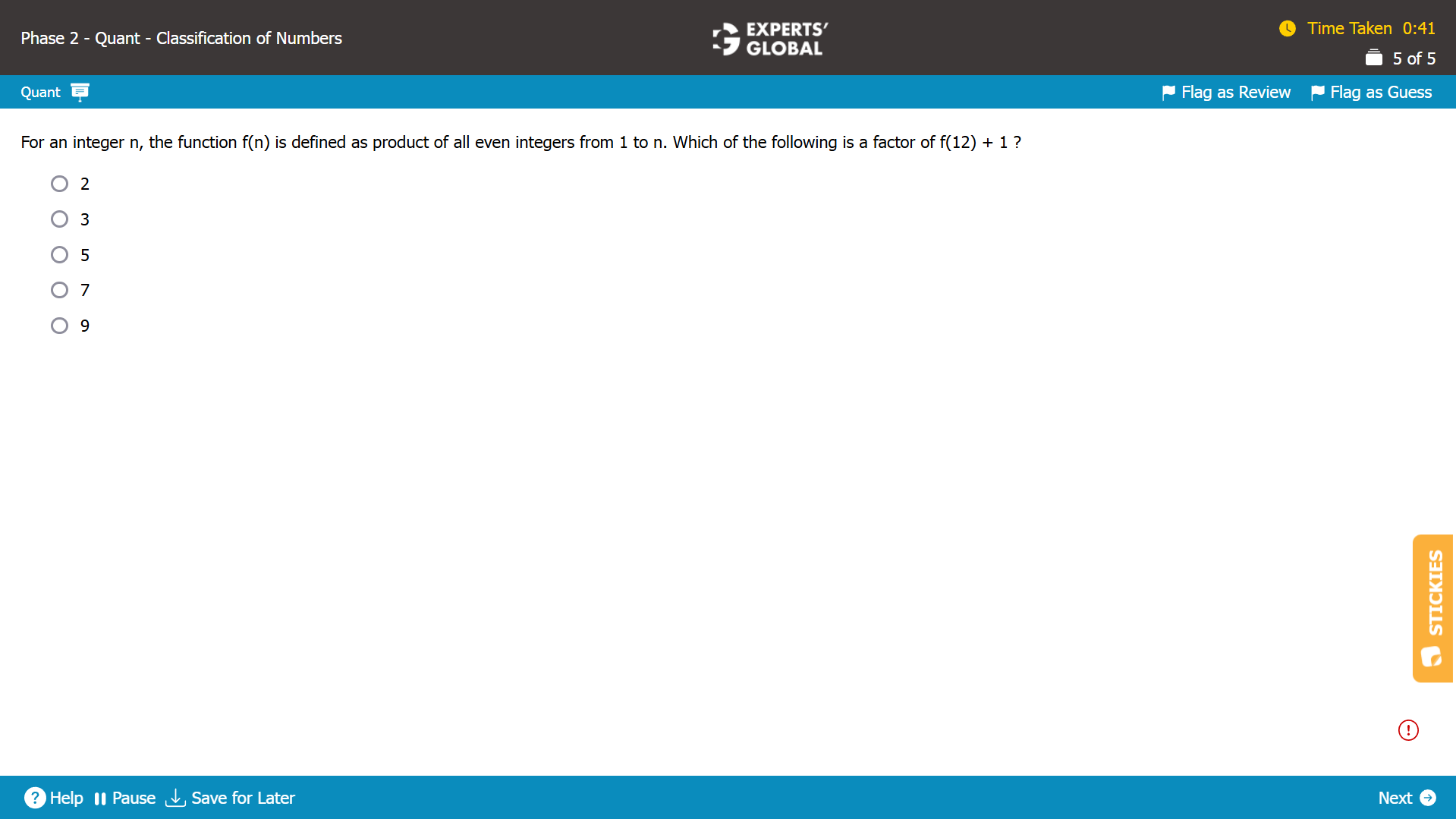
f(12) = 2 X 4 X 6 X 8 X 10 X 12 = 46080
f(12) + 1 = 46081
46081 is odd; so, 2 cannot be a factor.
The digits of 46081 add up to 4 + 6 + 0 + 8 + 1 = 19. 19 is not a multiple of 3. So, 3 cannot be a factor.
Additionally, 3 cannot be a factor of 46081. So, 9 cannot be a factor.
The last digit of 46081 is neither 0 nor 5. So, 5 cannot be a factor.
The only possible factor from the given answer choice is 7.
It can be verified that 46081 / 7 = 6583
7 is a factor of f(12) + 1.
[Alternatively….
f(12) = 2 X 4 X 6 X 8 X 10 X 12
f(12) +1 = (2 X 4 X 6 X 8 X 10 X 12) + 1
2 is a factor of f(12). So, 2 cannot be a factor of f(12) + 1.
3 is a factor of f(12). So, 3 cannot be a factor of f(12) + 1.
Additionally, 9 cannot be a factor of f(12) + 1.
10 is a factor of f(12). So, 10 cannot be a factor of f(12) + 1. As a result, 5 cannot be a factor of f(12) + 1.
The only possible factor from the given answer choice is 7.
It can be verified that 46081 / 7 = 6583
7 is a factor of f(12) + 1.]
D is the correct answer choice.
GMAT Remainders: Practice Question 3
Written Explanation
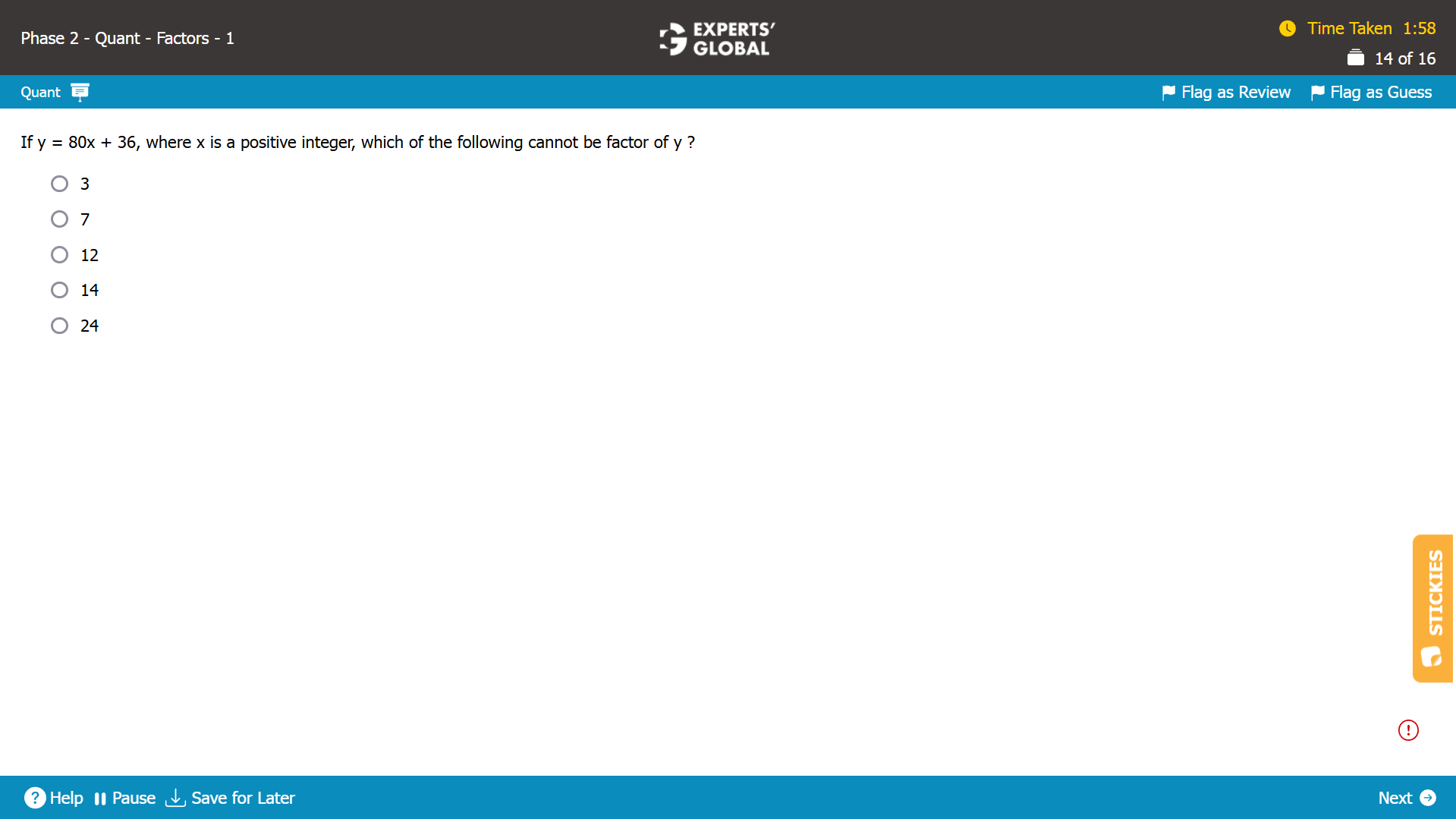
y = 80x + 36
Checking whether 3 can be a factor of y…
3 is a factor of 36.
If x is a multiple of 3, 3 will be a factor of 80x. So, 3 will be a factor of 80x + 36.
For example, if x = 3, y = 80x + 36 = 240 + 36 = 276 = 3 X 92.
3 can be a factor of y.
Checking whether 7 can be a factor of y…
36 is one more than a multiple of 7.
So, for y to be a multiple of 7, (80x + 1) will have to be a multiple of 7.
If x is 2, 80x + 1 = 160 + 1 = 161 = 23 X 7.
In that case, y = 80x + 36 = 160 + 36 = 196 = 28 X 7.
7 can be a factor of y.
Checking whether 12 can be a factor of y…
12 is a factor of 36.
If x is a multiple of 12, 12 will be a factor of 80x. So, 12 will be a factor of 80x + 36.
For example, if x = 12, y = 80x + 36 = 960 + 36 = 996 = 12 X 93.
12 can be a factor of y.
Checking whether 14 can be a factor of y…
36 is 8 more than a multiple of 14.
So, for y to be a multiple of 14, (80x + 8) will have to be a multiple of 14.
If x is 2, 80x + 8 = 160 + 8 = 168 = 12 X 14.
In that case, y = 80x + 36 = 160 + 36 = 196 = 14 X 14.
14 can be a factor of y.
Checking whether 24 can be a factor of y…
36 is 12 more than a multiple of 24.
So, for y to be a multiple of 24…
(80x + 12) will have to be a multiple of 24.
80x will have to leave a remainder of 12, 12 + 24, 12 + 2(24)… when divided by 24.
The possible remainders are {12, 36, 60, 84…}
80x is a multiple of 80 and will never fall in this series.
So, (80x + 12) cannot be a multiple of 24.
Overall, y cannot be a multiple of 24, or 24 cannot be a factor of y.
E is the correct answer choice.
GMAT Remainders: Practice Question 4
Written Explanation
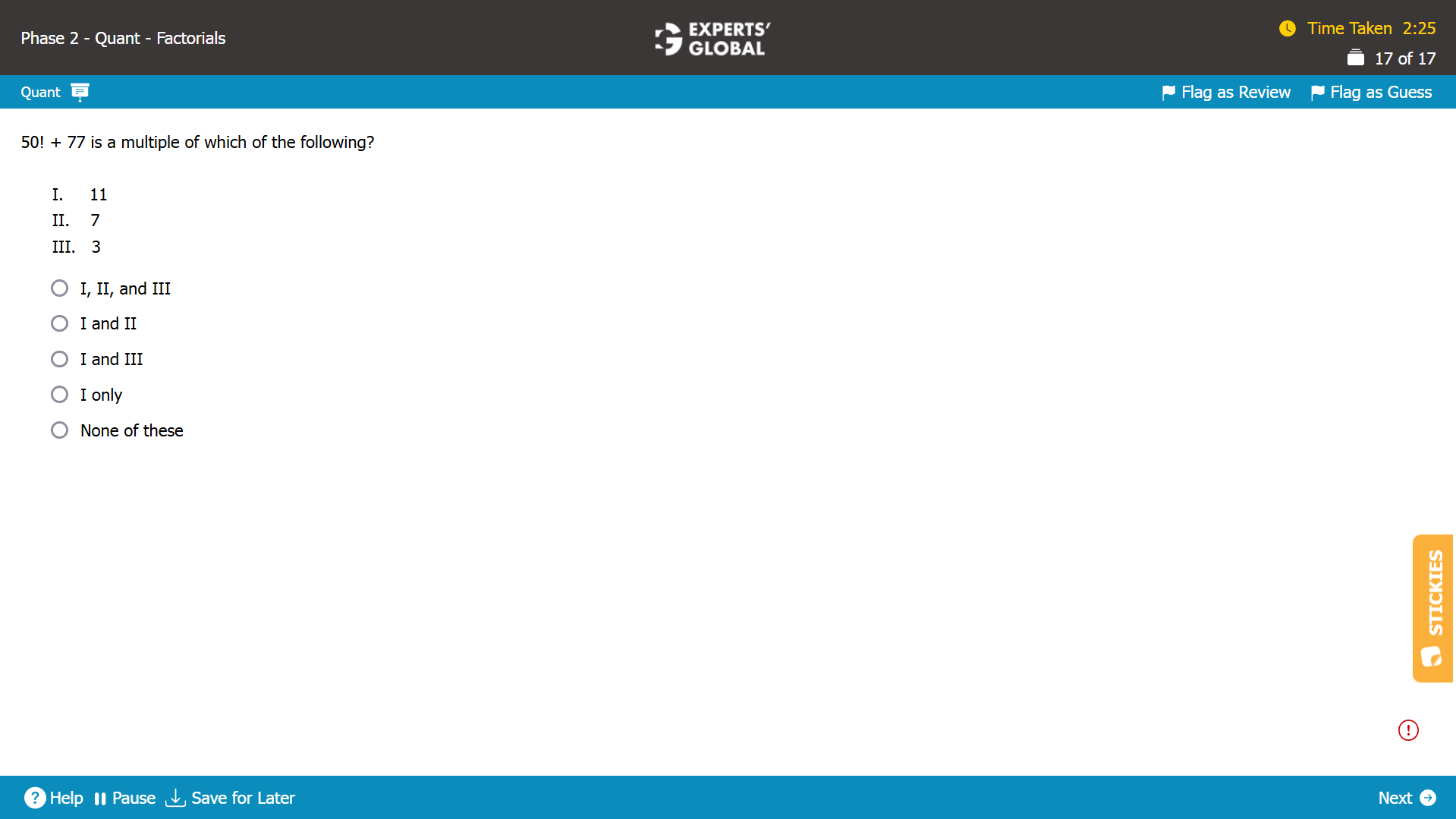
50! is a multiple of 11.
77 is a multiple of 11.
(50! + 77) will be a multiple of 11.
50! is a multiple of 7.
77 is a multiple of 7.
(50! + 77) will be a multiple of 7.
50! is a multiple of 3.
77 is NOT a multiple of 3.
(50! + 77) will NOT be a multiple of 3.
B is the correct answer choice.
GMAT Remainders: Practice Question 5
Written Explanation
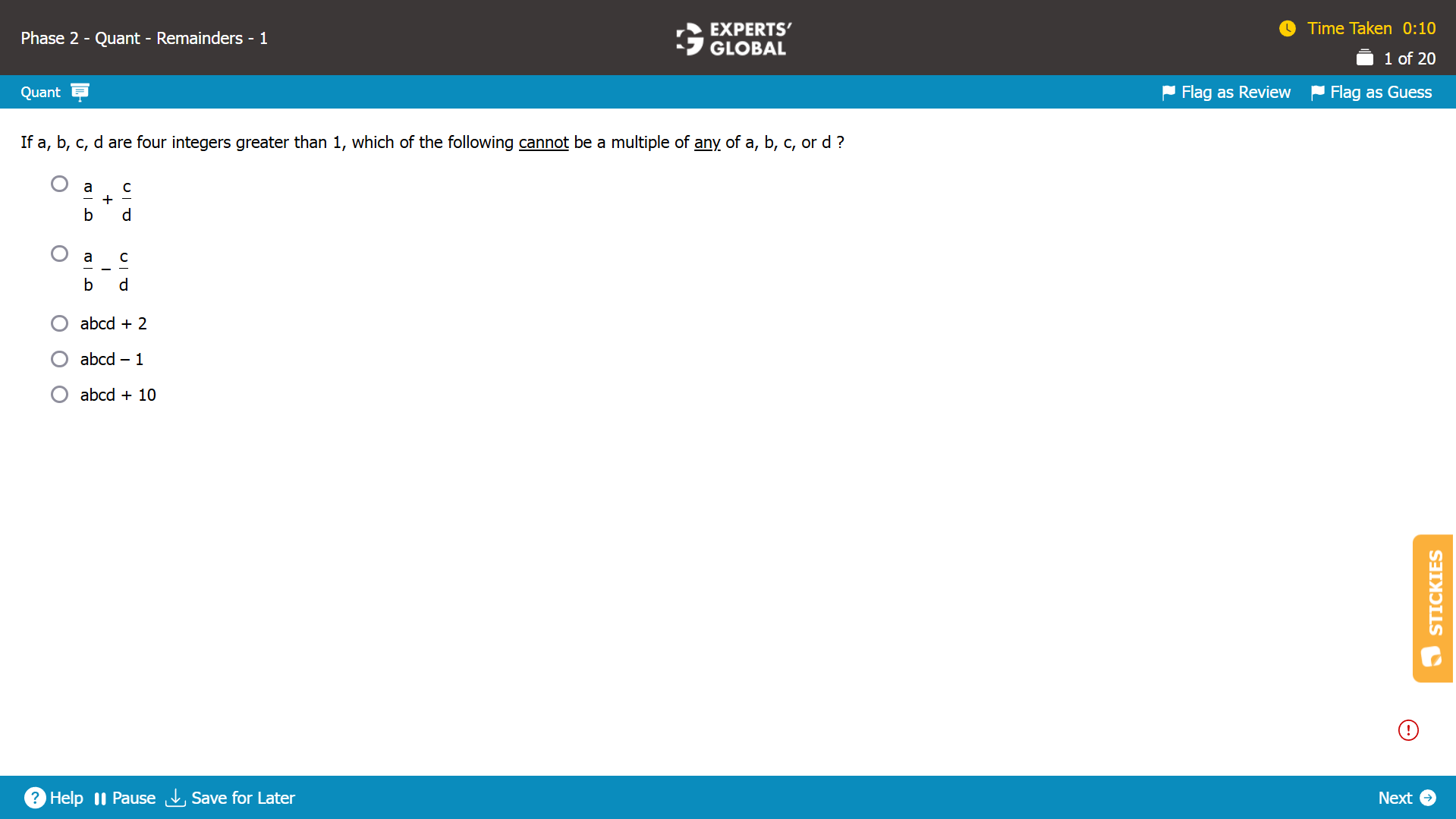
A.
Let’s say that a = b = c = d = 2.
a / b + c / d = 2 / 2 + 2 / 2 = 2.
2 is a multiple of a, b, c, and d.
(a / b + c / d) can be the multiple of a or b or c or d. Incorrect.
B.
Let’s say that a = c = 8 and b = 2 and d = 4.
a / b + c / d = 8 / 2 – 8 / 4 = 4 – 2 = 2.
2 is a multiple of b.
(a / b – c / d) can be the multiple of b. Incorrect.
C.
Let’s say that a = b = c = d = 2.
abcd + 2 = (2 X 2 X 2 X 2) + 2 = 18.
2 is a multiple of a, b, c, and d.
abcd + 2 can be the multiple of a or b or c or d. Incorrect.
D.
abcd will be a multiple of all of a, b, c, d.
None of a, b, c, d can be equal to 1.
So, abcd – 1 CANNOT be the multiple of ANY of of a, b, c, d. Correct.
E.
Let’s say that a = b = c = d = 2.
abcd + 10 = (2 X 2 X 2 X 2) + 10 = 26.
26 is a multiple of a, b, c, and d.
abcd + 10 can be the multiple of a or b or c or d. Incorrect.
D is the correct answer choice.
GMAT Remainders: Practice Question 6
Written Explanation
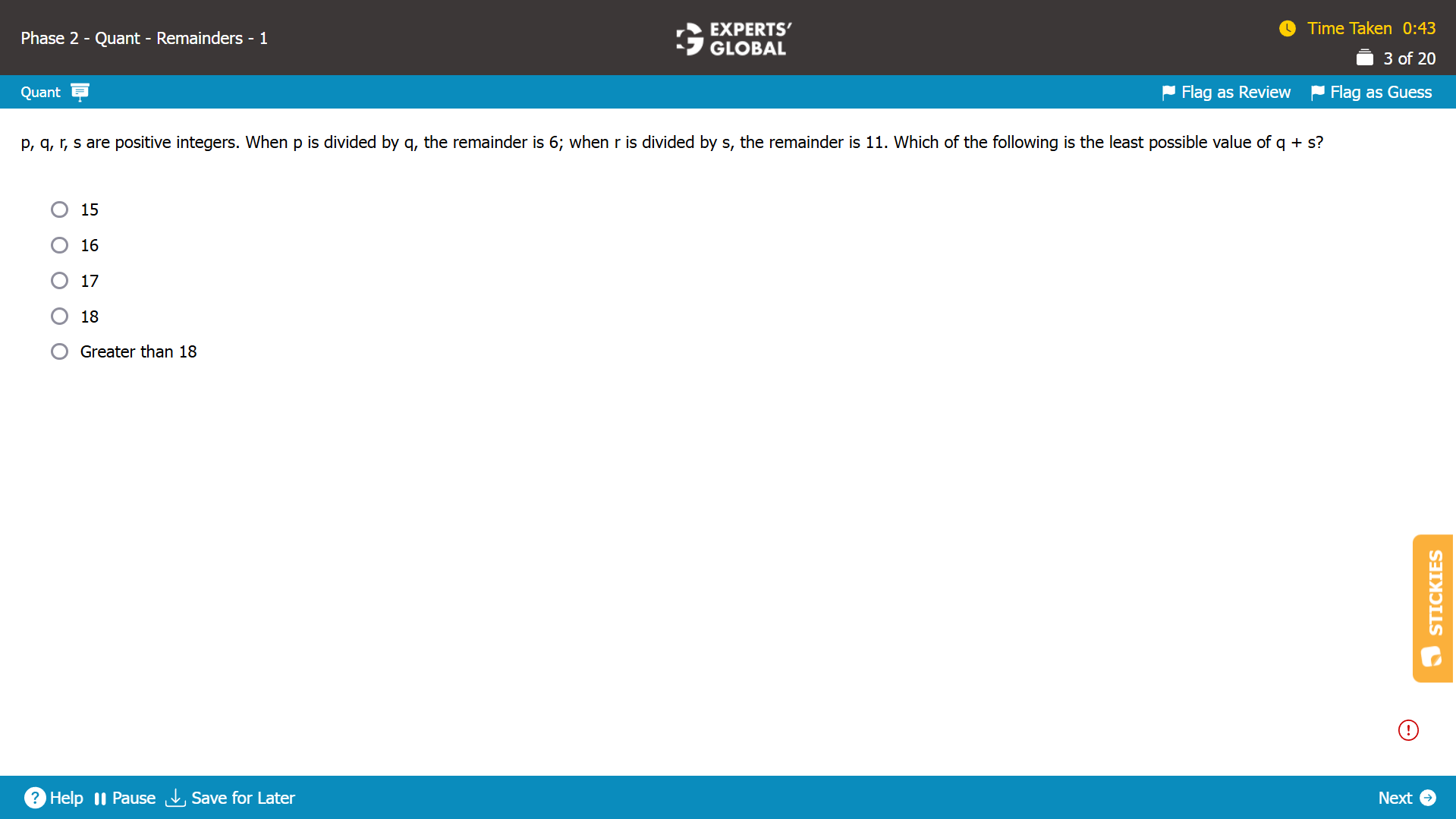
The remainder is always smaller than the divisor.
When p is divided by q, the remainder is 6.
So, q is greater than 6, or at least 7.
When r is divided by s, the remainder is 11.
So, s is greater than 11, or at least 12.
Overall, the least possible value of (q + s) is (7 + 12) = 19, or greater than 18.
E is the correct answer choice.
GMAT Remainders: Practice Question 7
Written Explanation
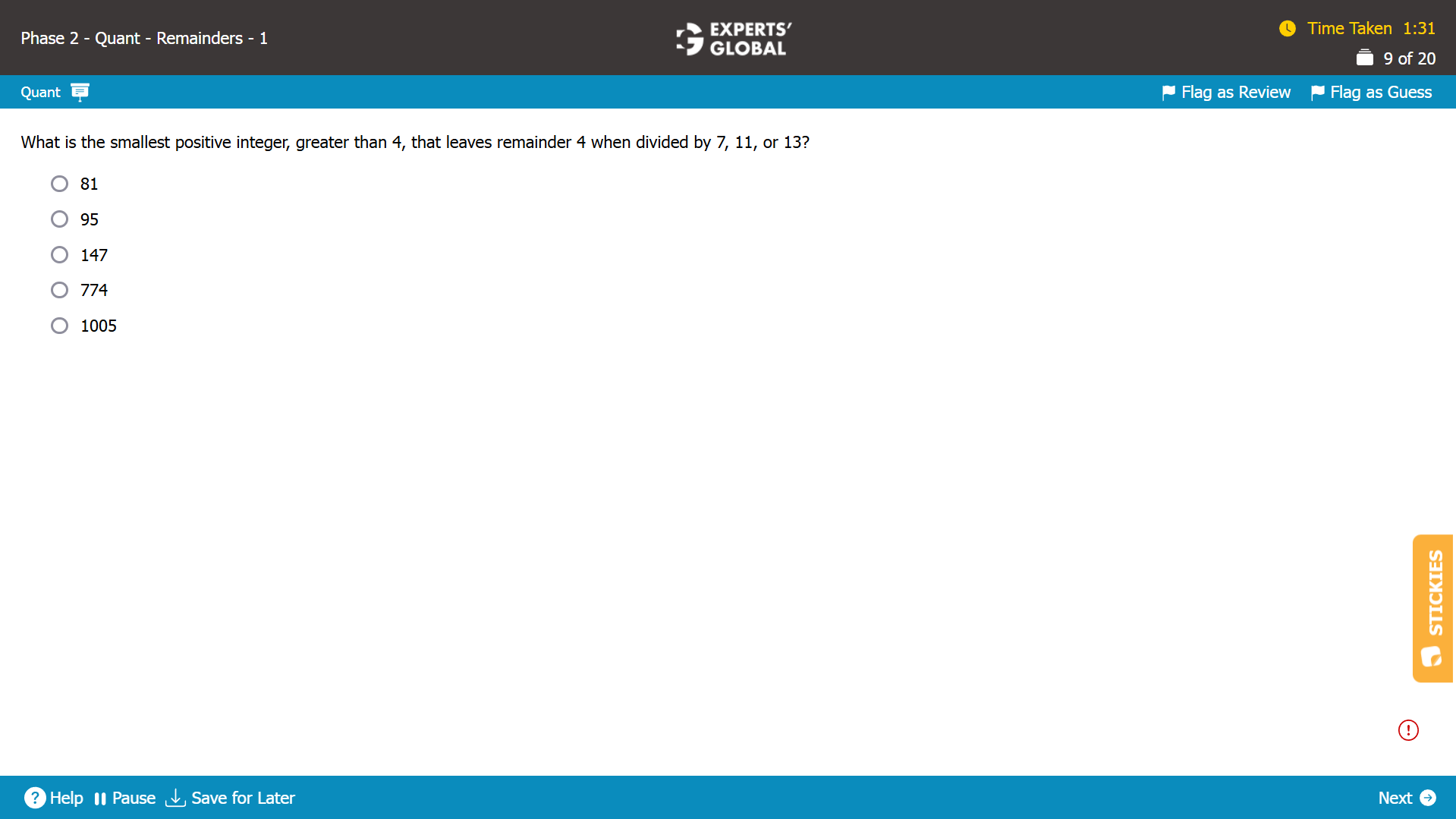
The smallest number to leave the remainder of 4 when divided by X, Y, Z = 4 + LCM of {X, Y, Z}.
So, smallest number to leave the remainder of 4 when divided by 7, 11, 13 = 4 + LCM of {7, 11, 13}
LCM of the {7, 11, 13} = 7 X 11 X 13 = 1001.
1001 is the smallest number of leave the remainder of 0 when divided by 7, 11, 13.
So, 1001 + 4 = 1005 is the smallest number of leave the remainder of 4 when divided by 7, 11, 13.
E is the correct answer choice.
GMAT Remainders: Practice Question 8
Written Explanation
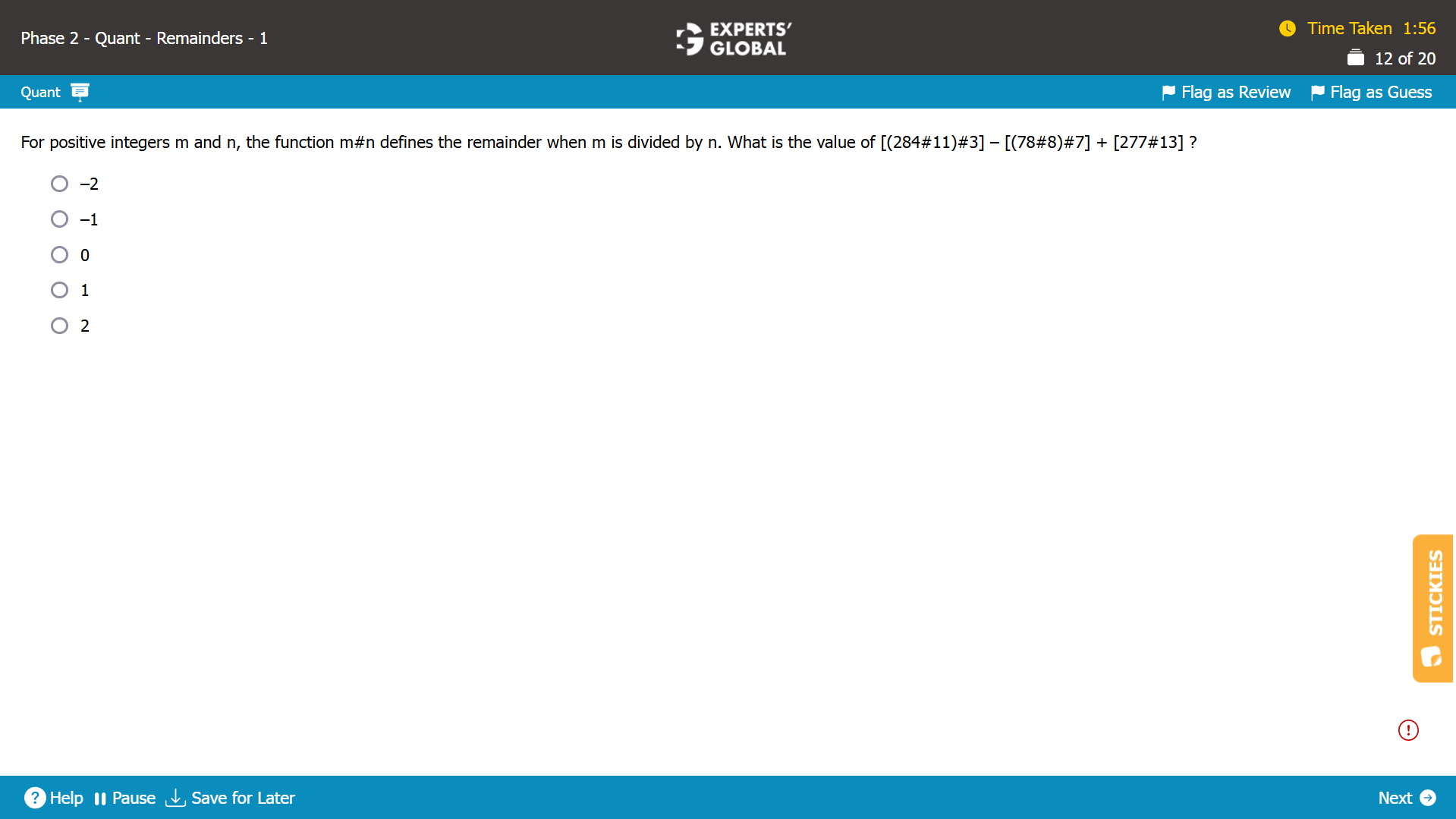
284#11 = remainder when 284 is divided by 11 = 9.
(284#11)#3) = (9#3) = remainder when 9 is divided by 3 = 0.
78#8 = remainder when 78 is divided by 8 = 6.
(78#8)#7) = (6#7) = remainder when 6 is divided by 7 = 6.
277#13 = remainder when 277 is divided by 13 = 4.
Overall,
[(284#11)#3] – [(78#8)#7] + [277#13] = [0 – 6 ] + 4 = –2.
A is the correct answer choice.
GMAT Remainders: Practice Question 9
Written Explanation
Let’s say that the smallest number is x.
x leaves a remainder of 8 when divided by 9. So, (x – 8) is a multiple of 9.
The next multiple would be (x – 8 + 9) = (x + 1).
x leaves a remainder of 9 when divided by 10. So, (x – 9) is a multiple of 10.
The next multiple would be (x – 9 + 10) = (x + 1).
x leaves a remainder of 10 when divided by 11. So, (x – 10) is a multiple of 11.
The next multiple would be (x – 10 + 11) = (x + 1).
x leaves a remainder of 11 when divided by 12. So, (x – 11) is a multiple of 12.
The next multiple would be (x – 11 + 12) = (x + 1).
Overall, (x + 1) is a multiple of 9, 10, 11, and 12.
The smallest value of (x + 1) = LCM of {9, 10, 11, 12} = 1980.
So, x = 1980 – 1 = 1979.
1979 = 1976 + 3 = 13 X 152 + 3.
So, the remainder when 1979 is divided by 13 is 3.
D is the correct answer choice.
GMAT Remainders: Practice Question 10
Written Explanation
Let’s say that N = ax X by X cz … where a, b, c… are prime factors of N and x, y, z… are positive integers.
Number of factors of N = (x + 1) X (y + 1) X (z + 1)…
12 = 2 X 2 X 3.
So, if W has 12 factors, there are the following possibilities.
Possibility 1: 12 is expressed as 2 X 2 X 3.
W = P1 X P2 X P32 where P1, P2, P3 are prime factors of W.
Number of factors of W = (1 + 1) X (1 + 1) X (2 + 1) = 2 X 2 X 3 = 12
The smallest value for W can be obtained by taking the smallest prime numbers.
P3 is raised to a higher power than P1 and P2. So, P3 needs to be the smallest prime number.
So, the smallest value of W = 5 X 3 X 22 = 60.
Possibility 2: 12 is expressed as 4 X 3 (or 3 X 4).
W = P13 X P22 where P1 and P2 are prime factors of W.
Number of factors of W = (3 + 1) X (2 + 1) = 4 X 3 = 12
The smallest value for W can be obtained by taking the smallest prime numbers.
P1 is raised to a higher power than P2. So, P1 needs to be the smallest prime number.
So, the smallest value of W = 23 X 32 = 72.
This value of W is greater than the value of W obtained in Possibility 1. So, Possibility 2 needs to be ignored.
Overall, the smallest value of W = 60 = 5 X 11 + 5.
Remainder when W is divided by 11 is 5.
B is the correct answer choice.
How and Where to Practice GMAT-style Remainders Problems
Among the few truly reliable sources for GMAT remainders problems are the official practice materials from GMAC and the Experts’ Global GMAT course. Within the Experts’ Global GMAT online preparation course, every remainder problem is presented on a GMAT-like interface that mirrors all the real exam tools and features. You will work through over 75 remainder questions in quizzes and complete 15 full-length GMAT mock tests, each containing a variety of remainder problems in the same distribution and proportion as they appear on the actual exam.
All the best!
