Last digits problems frequently appear on the GMAT and should be thoroughly covered in any comprehensive GMAT preparation course. These questions can feel bulky, but by understanding the periodicity of powers and recognizing repeating cycles in numbers, solving them becomes much simpler. Let’s dive into the concept and explore how to break down these problems step by step, making the process more straightforward and efficient.
Finding the Last Digit in Large Multiplications
(Example: What is the units digit of the numeric value of 1439 x 729 x 4537 x 9993 x 8054 x 779 x 8865?)
Large multiplications can be simplified by focusing only on the units digit. You don’t need to expand every term. By tracking the last digits of the numbers, you can quickly determine the final product. This approach saves time and increases accuracy. Watch the video below to see this concept in action and how it appears on the GMAT.
Finding the Last Digit in Large Multiplications
Finding Last Two Digits in Large Multiplications
(Example: What are the last two digits of the numeric value of 1243 x 9775 x 5423 x 999 x 8002 x 7779?)
When asked for the last two digits of a large product, you don’t need to multiply everything. Instead, focus on the last two digits of each factor and look for patterns. This approach makes solving these problems quick and efficient. Check out the video below to see how this concept works and how it’s tested on the GMAT.
Finding Last 2 Digits in Large Multiplications
Finding the Units Digit of Large Exponents
(Example: Finding units digit of 289873)
Questions asking for the last digit of a large power are straightforward once you know the approach. For example, numbers like 39167 can seem tricky, but the key is focusing on the units digit. Units digits follow a repeating cycle every four powers, so dividing the exponent by 4 provides an easy shortcut. After finding the remainder, raise the last digit to that power to get the result. With clear concepts and practice, this method becomes second nature. The video below demonstrates this process with simple explanations and GMAT-style examples.
Finding the Units Digit of Large Exponents
GMAT-style Last Digits Questions with Explanations
GMAT Last Digits Problems: Practice Question 1
Written Explanation
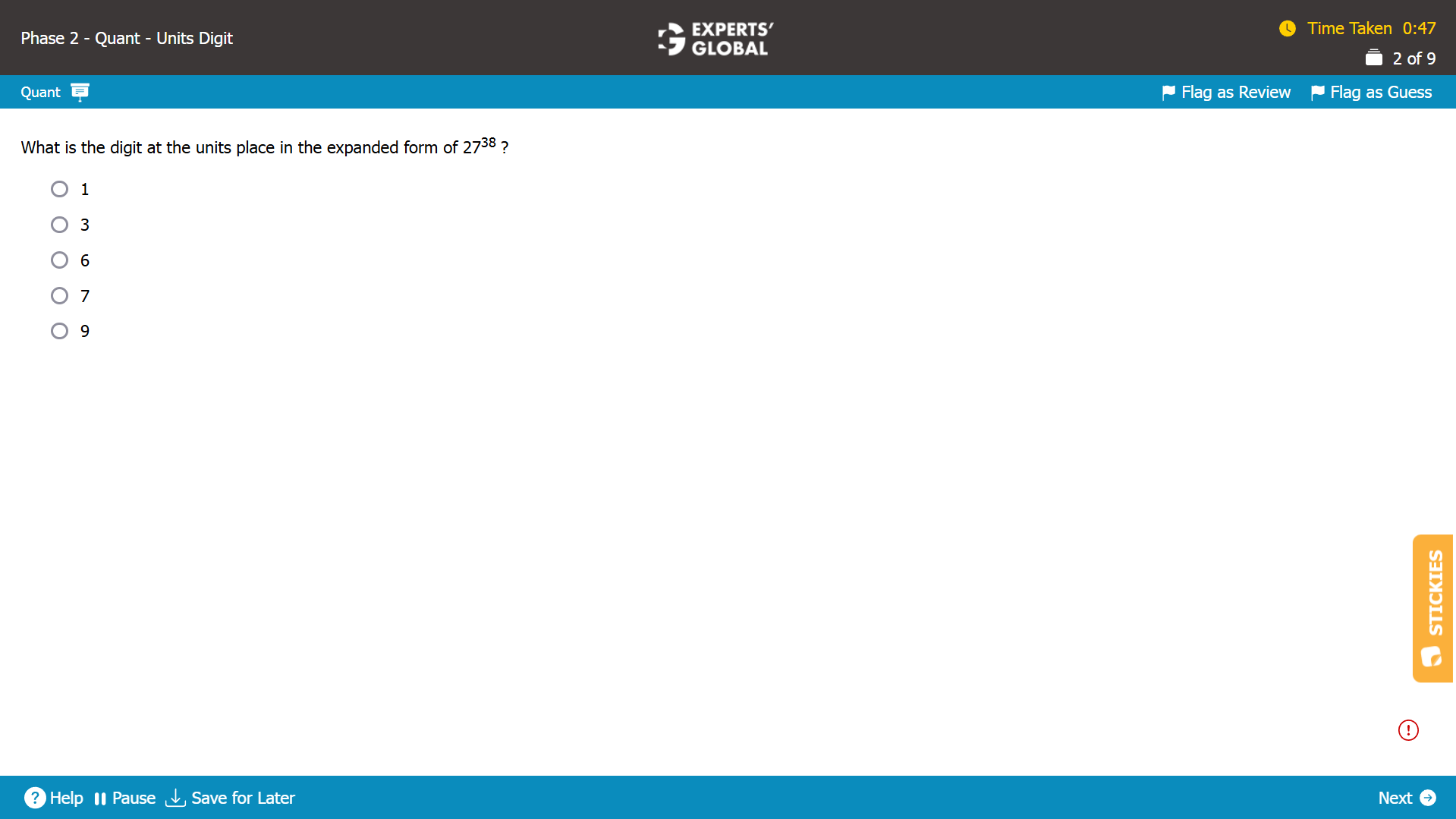
The last digit of 2738 will be the same as the last digit of 738.
71 = 7 has last digit 7.
72 will have last digit of 7 X 7 = last digit of 49 = 9.
73 will have last digit of 9 X 7 = last digit of 63 = 3.
74 will have last digit of 3 X 7 = last digit of 21 = 1.
75 will have last digit of 1 X 7 = last digit of 7= 7.
From the 5th power onwards, the last digits will repeat in the {7, 9, 3, 1} cycle with 4 terms.
38 = 4 X 9 + 2; so, 38 leaves the remainder of 2 in the cycle of 4.
So, the 38 – 2 = 36th power will complete 9 cycles of {7, 9, 3, 1}, and …
The 37th power will have the last digit of 7, the first term in the cycle.
The 38th power will have the last digit of 9, the second term in the cycle.
The last digit of 2738 is 9.
E is the correct answer choice.
GMAT Last Digits Problems: Practice Question 2
Written Explanation
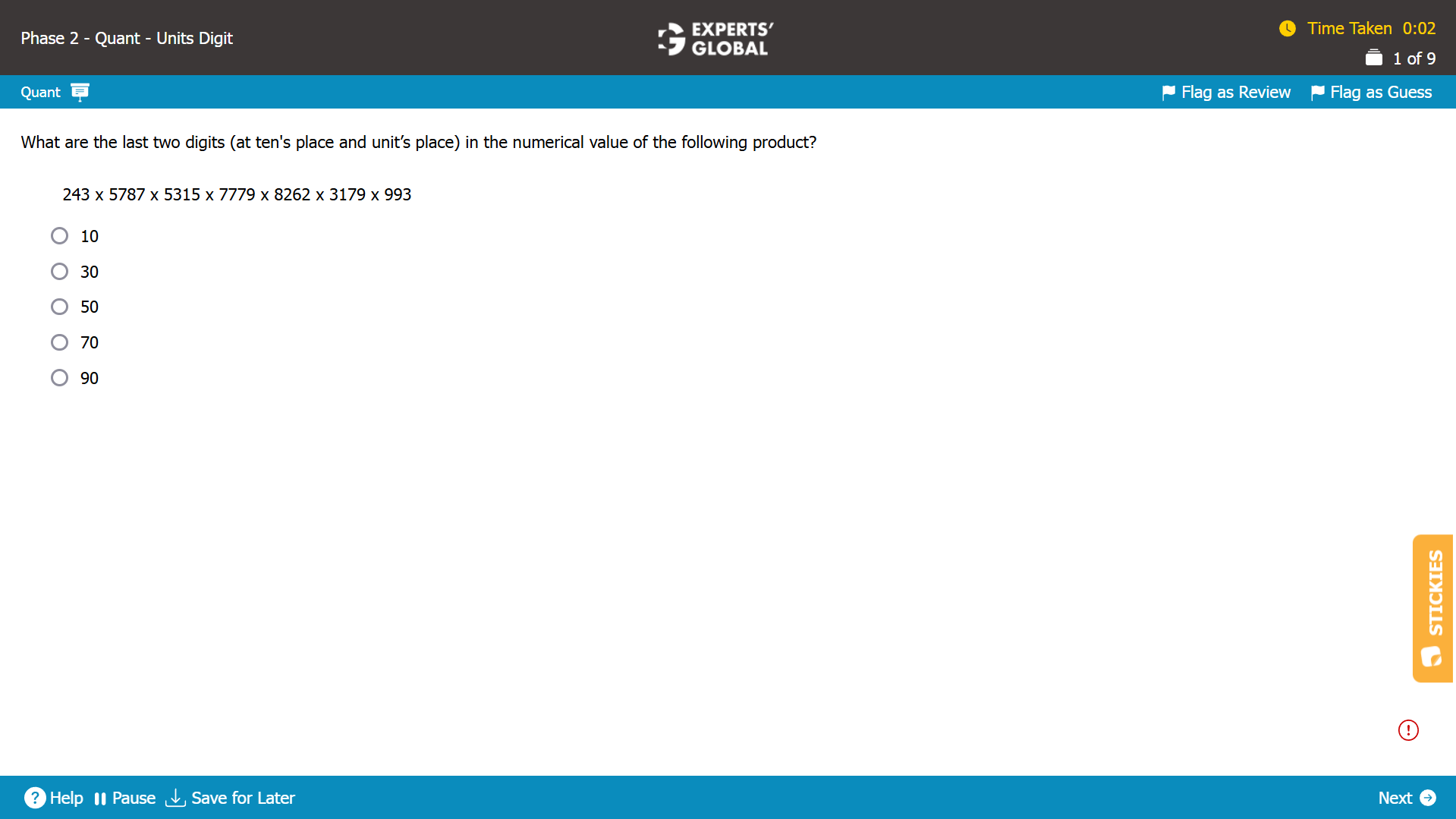
243 * 5787 * 5315 * 7779 * 8262 * 3179 * 993.
In the product, we have a 5 and a 2 at the last digits of individual elements. That will always give us a zero as the last digit of the entire product. Let’s separate them out
i.e. Our product = 243 * 5787 * (1063*5) * 7779 * (4131*2) * 3179 * 993
= [243 * 5787 * 1063 * 7779 * 4131 * 3179 * 993] * (2*5).
The second last digit of this product will be the last digit of 3 * 7 * 3 * 9 * 1 * 9 * 3 = 9.
The required two last digits are 9 and 0.
Hence, E is the correct answer choice.
GMAT Last Digits Problems: Practice Question 3
Written Explanation
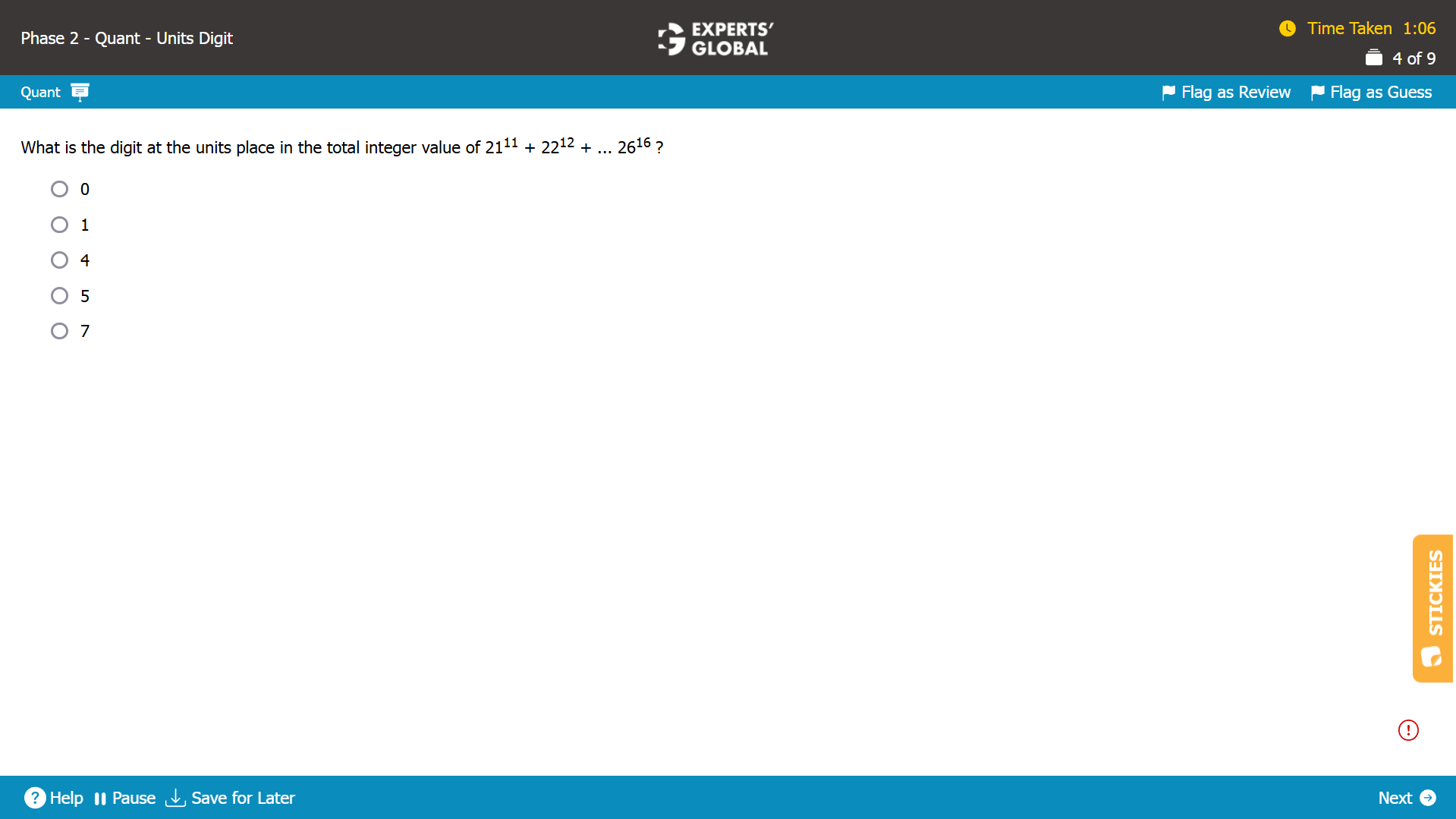
Units digit in the total integer value of (2111 + 2212 + … 2616 ) = Units digit in the sum of units digit in each term.
Let’s calculate the units digit in each term.
Units place digit of 2111
The units place digit of 2111 will be the same as the units place digit of 111 = units place digit of 1.
Units place digit of 2111 = 1.
Units place digit of 2212
The units place digit of 2212 will be the same as the units place digit of 212
21 = 2 has last digit 2.
22 will have last digit of 2 X 2 = last digit of 4= 4.
23 will have last digit of 4 X 2 = last digit of 8 = 8.
24 will have last digit of 8 X 2 = last digit of 16 = 6.
25 will have last digit of 6 X 2 = last digit of 12 = 2.
From the 5th power onwards, the last digits will repeat in the {2, 4, 8, 6} cycle with 4 terms.
12 = 4 X 3; so, the 12th power will complete 3 cycles of {2, 4, 8, 6}, and will have the last digit of 6, the fourth term in the cycle.
Units place digit of 2212 = 6.
Units place digit of 2313
The units place digit of 2313 will be the same as the units place digit of 313
31 = 3 has last digit 3.
32 will have last digit of 3 X 3 = last digit of 9 = 9.
33 will have last digit of 9 X 3 = last digit of 27 = 7.
34 will have last digit of 7 X 3 = last digit of 21 = 1.
35 will have last digit of 1 X 3 = last digit of 3= 3.
From the 5th power onwards, the last digits will repeat in the {3, 9, 7, 1} cycle with 4 terms.
13 = 4 X 3 + 1; so, 13 leaves the remainder of 1 in the cycle of 4.
So, the 13 – 1 = 12th power will complete 3 cycles of {3, 9, 7, 1}, and …
The 13thpower will have the last digit of 3, the first term in the cycle.
Units place digit of 2313 = 3.
Units place digit of 2414
The units place digit of 2414 will be the same as the units place digit of 414
41 = 4 has last digit 4.
42 will have last digit of 4 X 4 = last digit of 16 = 6.
43 will have last digit of 6 X 4 = last digit of 24 = 4.
From the 3rd power onwards, the last digits will repeat in the {4, 6} cycle with 2 terms.
14 = 7 X 2; so, the 14th power will complete 7 cycles of {4, 6}, and will have the last digit of 6, the second term in the cycle.
Units place digit of 2414 = 6.
Units place digit of 2515
The units place digit of 2515 will be the same as the units place digit of 515. Any power of 5 will have the units digit as 5.
Units place digit of 2515 = 5.
Units place digit of 2616
The units place digit of 2616 will be the same as the units place digit of 616. Any power of 6 will have the units digit as 6.
Units place digit of 2616 = 6.
Overall,
Units digit in the total integer value of (2111 + 2212 + … 2616 ) = Units digit in the sum of units digit in each term
Units digit in the total integer value of (2111 + 2212 + … 2616 ) = Units digit in (1 + 6 + 3 + 6 + 5 + 6) = units digit in 17 = 7.
E is the correct answer choice.
GMAT Last Digits Problems: Practice Question 4
Written Explanation
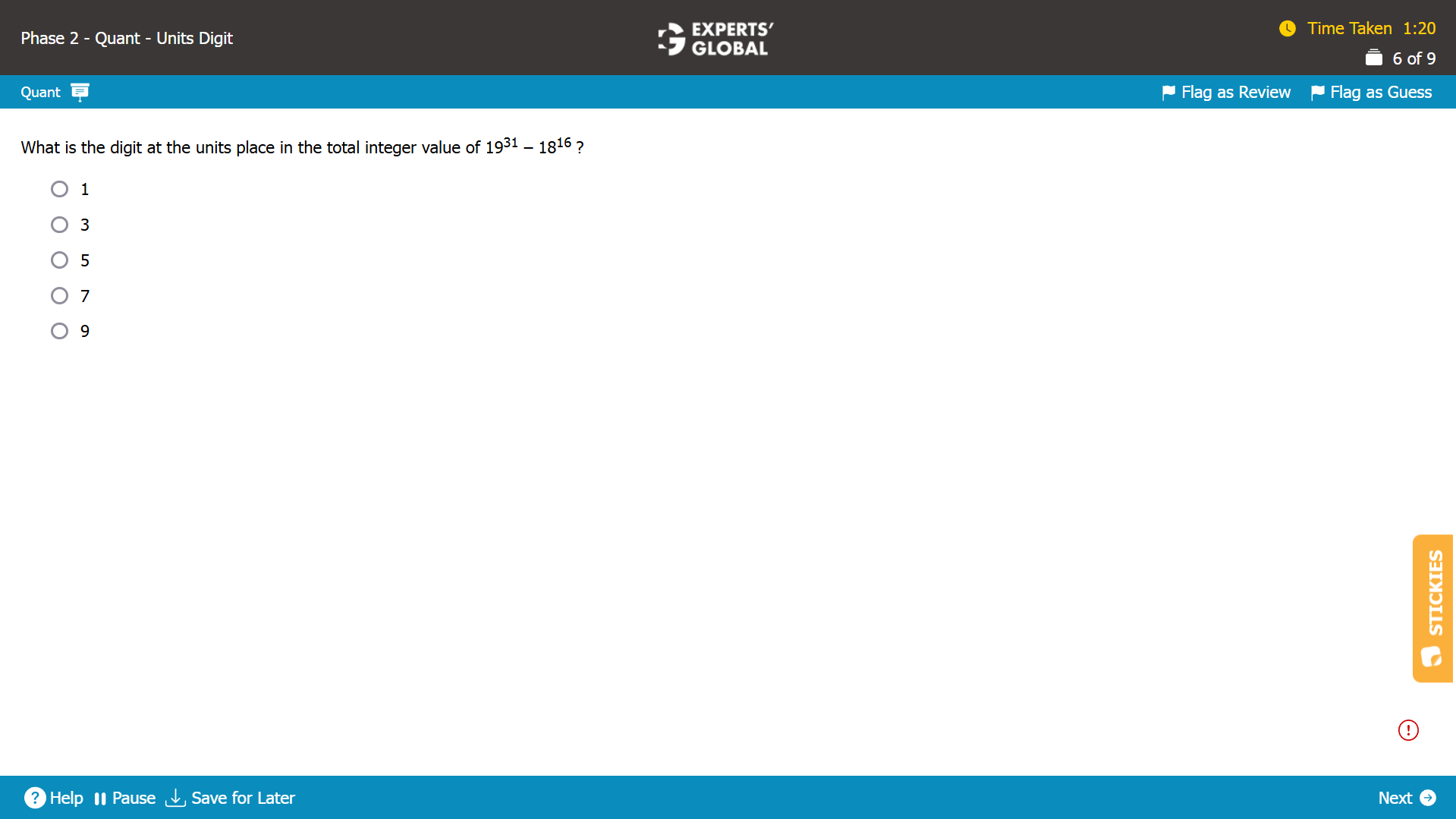
1931 has a greater base and a greater power than 1816.
So, 1931 > 1816.
Hence, units digit in the total integer value of 1931 – 1816 = units digit in 1931 – units digit in 1816.
Units digit in 1931 = units digit in 931.
91 = 9 has last digit 9.
92 will have last digit of 9 X 9 = last digit of 81 = 1.
93 will have last digit of 1 X 9 = last digit of 9 = 9.
From the 3rd power onwards, the last digits will repeat in the {9, 1} cycle with 2 terms.
31 = 2 X 15 + 1; so, 31 leaves the remainder of 1 in the cycle of 2.
So, the 31 – 1 = 30th power will complete 15 cycles of {9,1}, and the 31st power will have the units digit of 9, the first term in the cycle.
So, units digit in 931 = 9.
Units digit in 1816 = units digit in 816.
81 = 8 has last digit 8.
82 will have last digit of 8 X 8 = last digit of 64 = 4.
83 will have last digit of 4 X 8 = last digit of 32 = 2.
84 will have last digit of 2 X 8 = last digit of 16 = 6.
From the 5th power onwards, the last digits will repeat in the {8, 4, 2, 6} cycle with 4 terms.
16 = 4 X 4; so, the 16th power will complete 4 cycles of {8, 4, 2, 6}, and will have the units digit of 6, the fourth term in the cycle.
So, units digit in 816 = 6.
Overall.
Units digit in the total integer value of 1931 – 1816 = units digit in 1931 – units digit in 1816
= 9 – 6
= 3.
Units digit in the total integer value of 1931 – 1816 will be 3.
B is the correct answer choice.
GMAT Last Digits Problems: Practice Question 5
Written Explanation
16! = 1 X 2 X 3 … X 15 X 16.
Let’s find the prime factors of all numbers till 16.
2 = 2
3 = 3
4 = 2 X 2
5 = 5
6 = 2 X 3
7 = 7
8 = 2 X 2 X 2
9 = 3 X 3
10 = 2 X 5
11 = 11
12 = 2 X 2 X 3
13 = 13
14 = 2 X 7
15 = 3 X 5
16 = 2 X 2 X 2 X 2
The rightmost non-zero digit in 16! will be the last digit when all the powers of 10 have been removed from 16!
There are 3 5s and 15 2s in 16!. So, there are 3 powers of 10.
So, let’s remove…
2 and 5 for the first power of 10.
10 for the second power of 10.
5 from 15 and 2 from 16, for the third power of 10.
Now, 16! without any rightmost zeros will be the product of
3
4
6
7
8
9
11
12
13
14
3
8
The last digit of 16! without any rightmost zeros
= last digit of (3 X 4 X 6 X 7 X 8 X 9 X 11 X 12 X 13 X 14 X 3 X 8)
= last digit of (3 X 4 X 6 X 7 X 8 X 9 X 1 X 2 X 3 X 4 X 3 X 8)
= last digit of (3 X 4 X 6 X 7) X last digit of (8 X 9 X 1 X 2) X last digit of (3 X 4 X 3 X 8)
= last digit of (4 X 4 X 8)
= 8
The rightmost non-zero integer in the integer value of 16! is 8.
E is the correct answer choice.
GMAT Last Digits Problems: Practice Question 6
Written Explanation
1 / 55 = (1 / 5) X (1 / 11).
1 / 11 = 0.090909090… no terminating.
(1 / 5) X (1 / 11) = (1 / 5) X (0.090909090… no terminating) = 0.018181818…. no terminating.
It can be observed that ….
… the first digit after the decimal point is 0.
… the 2nd, 4th, 6th… digits after the decimal point are 1. So, all even digits after the decimal point are 1.
… the 3rd, 5th, 7th… digits after the decimal point are 8. So, all odd digits, except the first odd digit, after the decimal point are 8.
85th digit on the right of the decimal point would be an odd digit.
So, the 85th digit on the right of the decimal point in (1 / 55) would be 8.
D is the correct answer choice.
GMAT Last Digits Problems: Practice Question 7
Written Explanation
Last two digits of numerical value of 49852 + 1177 = Last two digits of 49852 + last two digits of 1177.
Last two digits of 49852 …
491 = 49 has last two digits of 49.
492 will have last two digits of 49 X 49 = last two digits of 2401 = 01.
493 will have last two digits of 01 X 49 = 49.
From the 3rd power onwards, the last two digits will repeat in the {49, 01} cycle with 2 terms.
852 = 426 X 2; so, the 852nd power will complete 426 cycles of {49, 01}, and will have the last two digits of 01, the second term in the cycle.
So, last two digits in 49852 = 01.
Last two digits of 1177 …
111 = 11 has last two digits of 11.
112 will have last two digits of 11 X 11 = last two digits of 121 = 21.
113 will have last two digits of 21 X 11 = last two digits of 231 = 31.
114 will have last two digits of 31 X 11 = last two digits of 341 = 41.
Similarly…
119 will have last two digits of 81 X 11 = last two digits of 891 = 91.
1110 will have last two digits of 91 X 11 = last two digits of 1001 = 01.
1111 will have last two digits of 01 X 11 = last two digits of 11 = 11.
From the 11th power onwards, the last two digits will repeat in the {11, 21, 31, ….91, 01} cycle with 10 terms.
77 = 7 X 10 + 7; so, 77 leaves the remainder of 7 in the cycle of 10.
So, the 77 – 7 = 70th power will complete 7 cycles of {11, 21, 31, ….91, 01}, and the 77th power will have the last digit of 71, the seventh term in the cycle.
So, last two digits in 1177 = 71.
Last two digits of numerical value of 49852 + 1177 = Last two digits of 49852 + last two digits of 1177 = 01 + 71 = 72.
The numerical value of 49852 + 1177 will have the last two digits of 72.
C is the correct answer choice.
How and Where to Practice GMAT-style Units Digits Problems
Reliable sources for GMAT units-digit problems include the official practice materials from GMAC and the Experts’ Global GMAT course. Within the Experts’ Global GMAT online preparation course, every units-digit problem is presented on a GMAT-like interface, using all the tools and features found on the actual exam. You will tackle more than 50 units-digit questions through quizzes and complete 15 full-length GMAT mock tests, each designed to include a mix of units-digit problems in the same distribution and proportion as those on the real GMAT.
All the best!
