Data Sufficiency, commonly known as DS, stands out as one of the most distinctive and engaging question types on the GMAT. Its format differs sharply from what most students see in routine academic settings, which explains why it can feel unfamiliar in the beginning. Rather than asking you to compute a final answer, a DS question asks you to decide whether the information given is enough to answer the question. At its core, the GMAT uses this format to assess how steadily and logically you evaluate sufficiency, not how fast you calculate. Within the 20 questions that make up the Data Insights section of the GMAT, about 5 to 7 are Data Sufficiency questions, making thorough coverage of DS an essential part of any reliable GMAT prep course.
On this page, we present a range of sample data sufficiency questions designed to give you direct exposure to how different concepts are tested through the data sufficiency question type on the GMAT. As you work through these questions, without worrying about speed, use this opportunity to gain first hand familiarity with the data sufficiency question format, flow, user interface, and the layers of logic that shape each question. Keep your focus on carefully engaging with the questions and the reasoning required to arrive at correct answers. Use this resource thoughtfully to build broad exposure to the GMAT data sufficiency question type in a short span, and carry these learnings forward into subsequent GMAT quizzes, GMAT sectional tests, and GMAT full-length mock tests. Happy practicing!
Important: Before visiting the Data Sufficiency sample questions, if you would like a quick brush up of key DS concepts, you may first visit: Free GMAT Data Sufficiency Prep
Data Sufficiency Sample Question 1
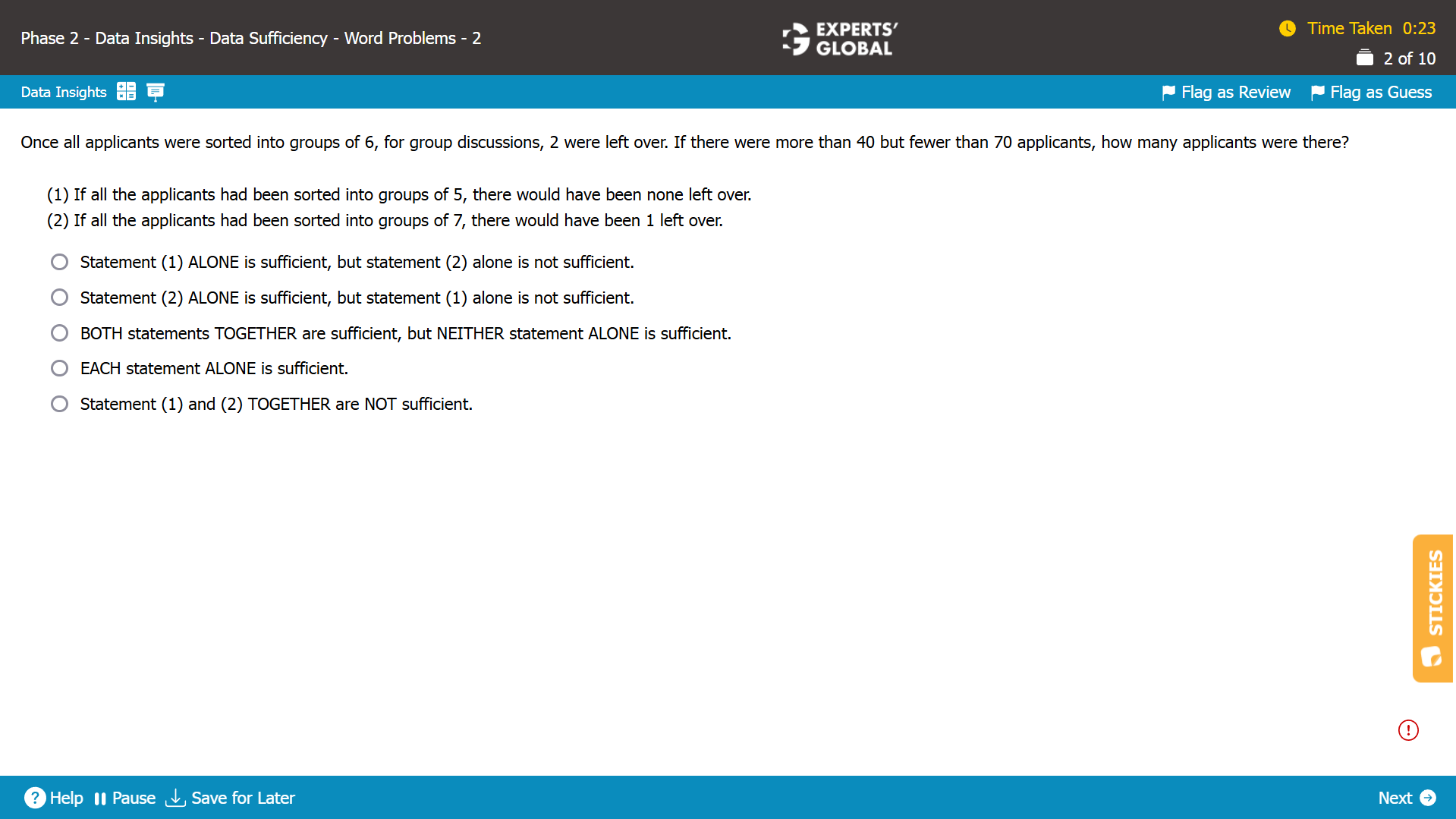
Hint:The required number is “6K + 2”; possibilities are: 44, 50, 56, 62, 68; each statement leads to “50” as only 50 among these possibilities satisfies the given conditions.
Detailed explanation:
Let the total number of applicants be N.
Since once all applicants were sorted into groups of 6, 2 were left over: N = 6p + 2, where p is some non-negative integer. (Equation I)
Since there were more than 40 but fewer than 70 applicants, 40 < N < 70. (Equation II)
We need to find whether the value of N can be determined.
Statement (1)
N = 5q + 0, where q is some non-negative integer. (Equation III)
The values of N that satisfy both Equation I and Equation II are 44, 50, 56, 62, and 68.
The values of N that satisfy both Equation I and Equation III are 45, 50, 55, 60, and 65.
The only value of N that satisfies Equations I, II, and III is 50.
It is possible to determine with certainty the value of N. Hence, Statement (1) is sufficient.
Statement (2)
N = 7r + 1, where r is some non-negative integer. (Equation IV)
The values of N that satisfy both Equation I and Equation II are 44, 50, 56, 62, and 68.
The values of N that satisfy both Equation I and Equation IV are 43, 50, 57, and 64.
The only value of N that satisfies Equations I, II, and IV is 50.
It is possible to determine with certainty the value of N. Hence, Statement (2) is sufficient.
D is the correct answer choice.
Data Sufficiency Sample Question 2
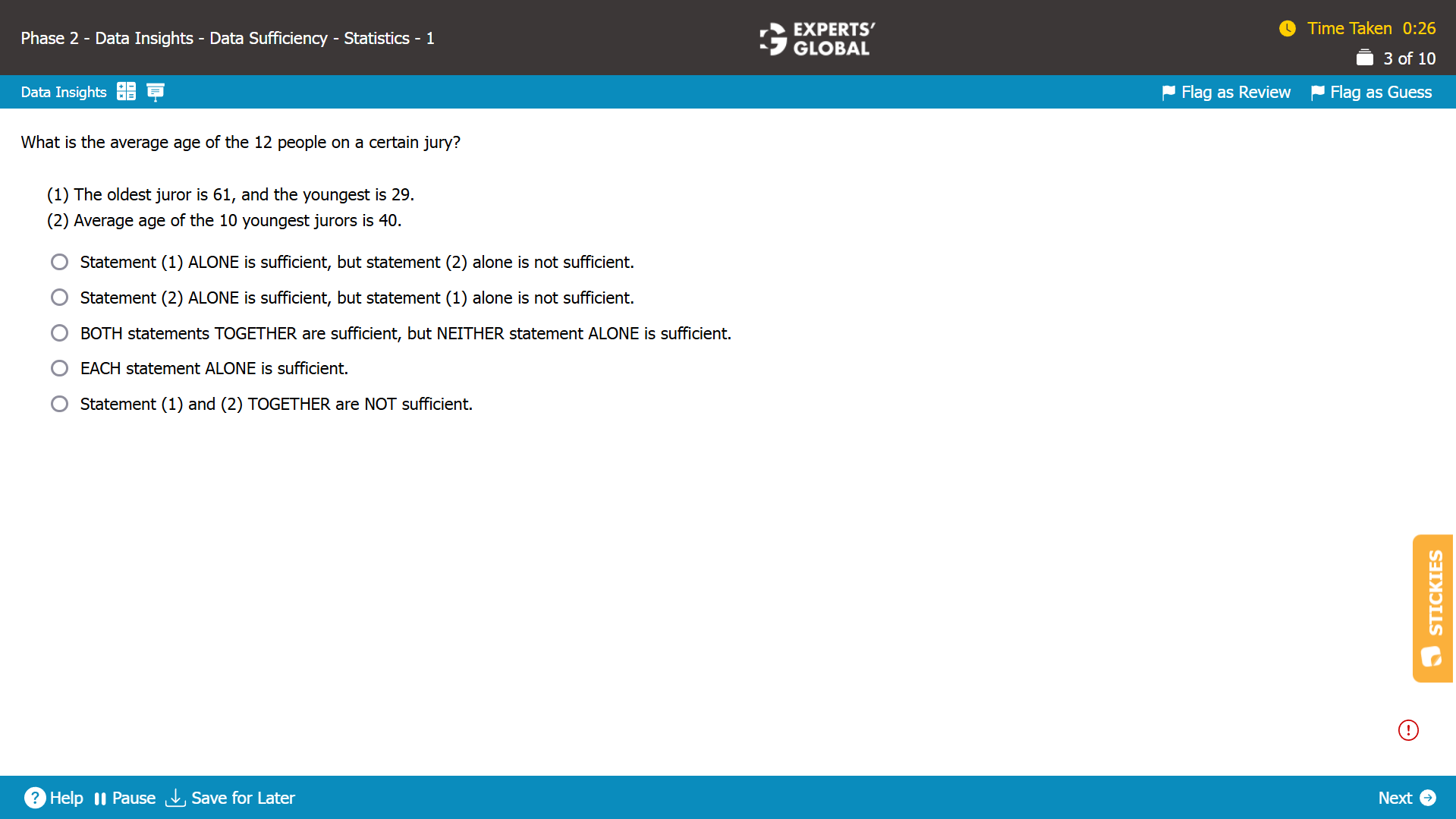
There are 12 people on a certain jury.
We need to find whether the average age of the jury can be determined.
Statement (1)
Since the average value of a set depends on all elements within that set and no information is provided regarding the ages of the middle 10 members, it is NOT possible to determine the exact average age of the jury. Hence, Statement (1) is insufficient.
Statement (2)
Since the average value of a set depends on all elements within that set and no information is provided regarding the ages of the oldest 2 members, it is NOT possible to determine the exact average age of the jury. Hence, Statement (2) is insufficient.
As Statement (1) alone as well as Statement (2) alone is insufficient to answer the question, we need to now combine the two statements.
Statement (1) and Statement (2) combined
The two statements combined give us no information regarding the age of the 11th youngest member.
It is NOT possible to determine the exact average age of the jury. Hence, Statement (1) and Statement (2) combined are insufficient.
E is the correct answer choice.
Data Sufficiency Sample Question 3
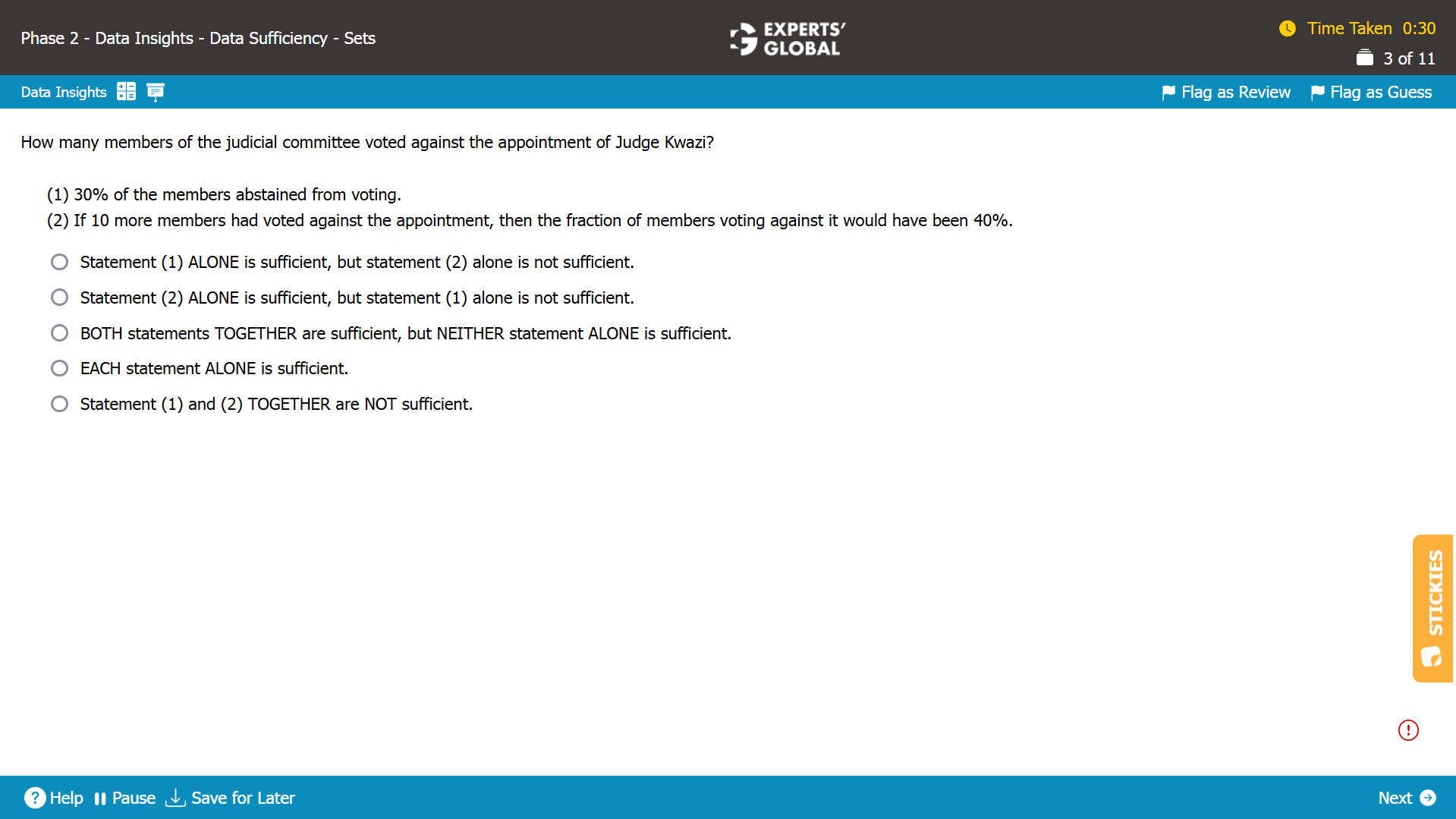
Let the number of people who did not vote be X.
Let the number of people who voted against the appointment of Judge Kwazi be A.
Let the number of people who voted in favor of the appointment of Judge Kwazi be B.
Total members in the judicial committee = X + A + B
We need to find whether the value of A can be determined.
Statement (1)
0.3(X + A + B) = X
Since we have 1 equation with 3 unknown variables it is not possible to determine the exact value of A. Hence, Statement (1) is insufficient.
Statement (2)
(A + 10) = 0.4(X + A + B)
Since we have 1 equation with 3 unknown variables it is not possible to determine the exact value of A. Hence, Statement (2) is insufficient.
As Statement (1) alone as well as Statement (2) alone is insufficient to answer the question, we need to now combine the two statements.
Statement (1) and Statement (2) combined
The two statements combined give us 2 equations with 3 unknown variables.
It is not possible to determine the exact value of A. Hence, Statement (1) and Statement (2) combined are insufficient.
E is the correct answer choice.
Data Sufficiency Sample Question 4
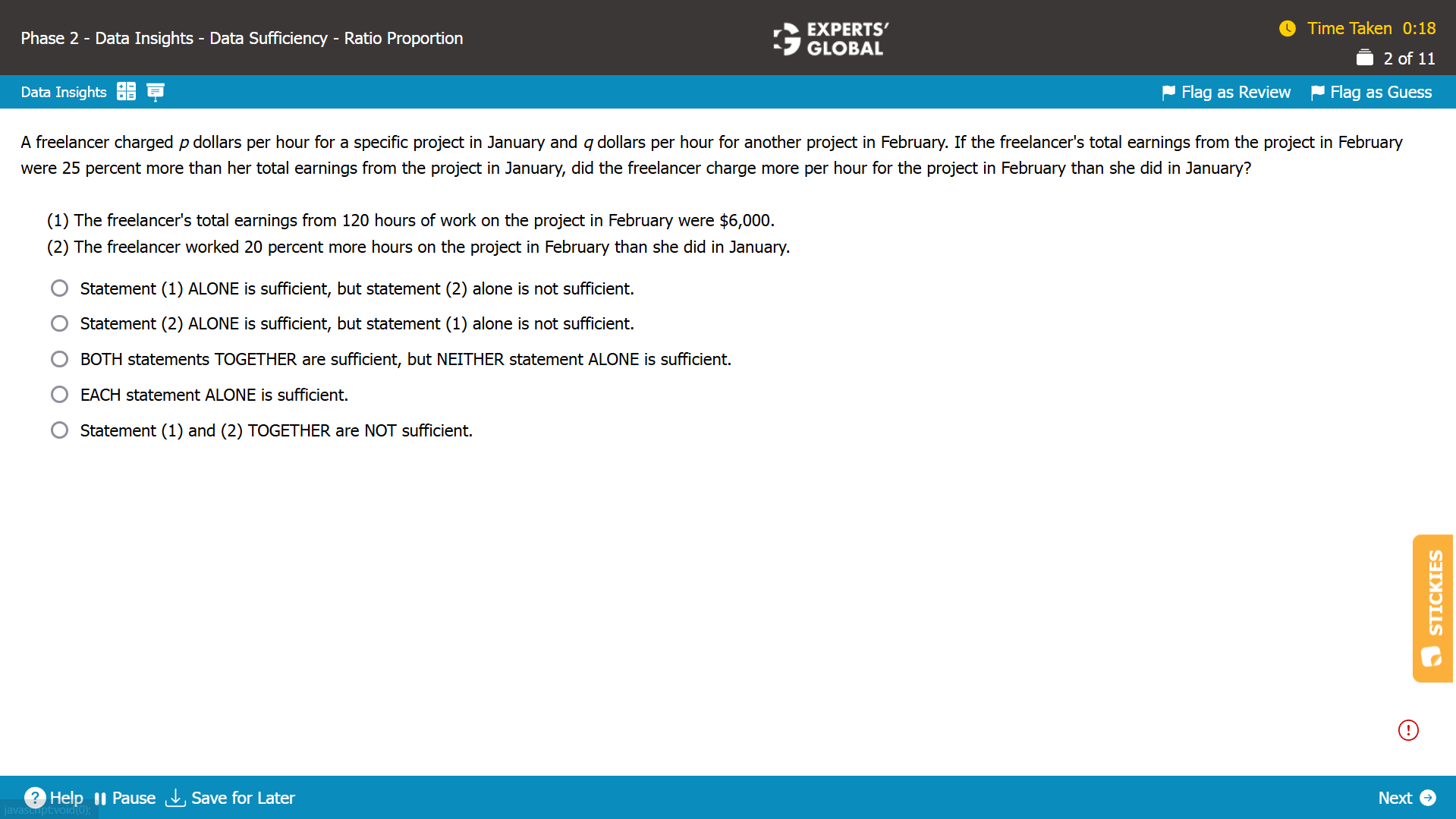
Let the total number of hours the freelancer worked in January be m.
Let the total number of hours the freelancer worked in February be n.
Since the freelancer charged p dollars per hour in January, total earnings in January = mp.
Since the freelancer charged q dollars per hour in February, total earnings in February = nq. Since the freelancer’s total earnings from the project in February were 25 percent more than her total earnings from the project in January:
nq = 1.25mp (Equation I)
We need to find whether q > p.
Statement (1)
Since n = 120 and nq = 6,000, it follows that q = 6,000 / 120 = 50.
From Equation I,
nq = 1.25mp
6,000 = 1.25mp
mp = 6,000 / 1.25
Since no information is provided regarding the values of m and p, it is NOT possible to determine with certainty whether q > p. Hence, Statement (1) is insufficient.
Statement (2)
n = 1.2m
Substituting the value of n into Equation I:
nq = 1.25mp
(1.2m)q = 1.25mp
Cancelling m from both sides:
1.2q = 1.25p
q = ( 1.25 / 1.2 ) p > p
It is possible to determine with certainty that q > p. Hence, Statement (2) is sufficient.
B is the correct answer choice.
Data Sufficiency Sample Question 5
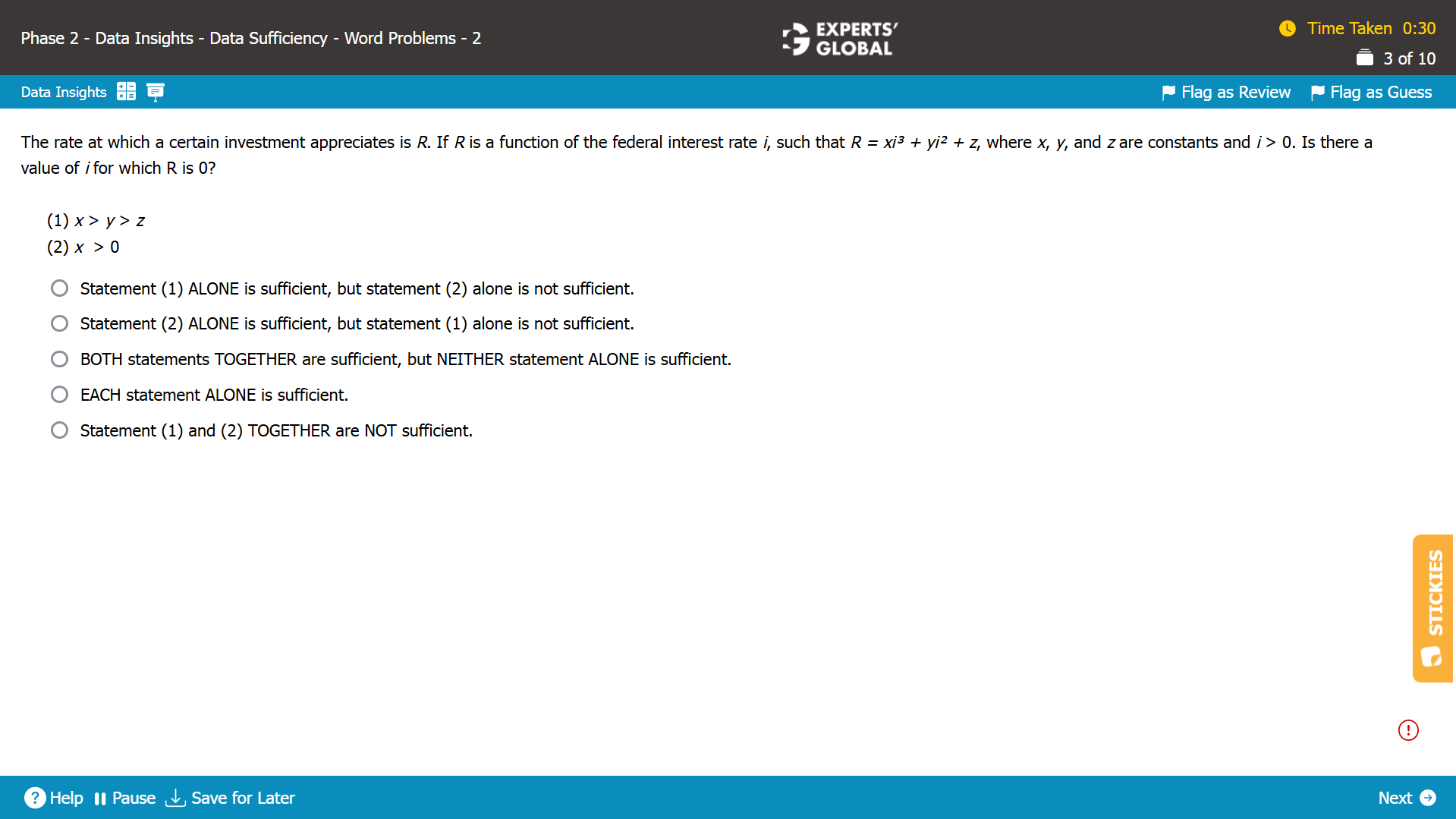
R = xi³ + yi² + z
The values of x, y, and z are unknown.
i > 0
We need to find whether there exists a value of i for which R is 0, which can also be expressed as:
We need to find whether there exists a value of i for which xi³ + yi² + z is 0.
Statement (1)
x > y > z
Possibility 1: If x = 1, y = 0, z = –1 and i = 1 , then R = xi³ + yi² + z = (1)(1)³ + (0)(1)² – 1 = 1 – 1 = 0. In this case, there exists a value of i for which R is 0.
Possibility 2: If x = 3, y = 2, and z = 1, then R = xi³ + yi² + z = (3)i³ + (2)i² + 1. In this case, R will NOT be 0 for any value of i > 0.
It is NOT possible to determine with certainty whether there exists a value of i for which R is 0. Hence, Statement (1) is insufficient.
Statement (2)
Similar reasoning as above can be applied using the same values for x, y, and z to show that it is NOT possible to determine with certainty whether there exists a value of i for which R is 0. Hence, Statement (2) is insufficient.
As Statement (1) alone as well as Statement (2) alone is insufficient to answer the question, we need to now combine the two statements.
Statement (1) and Statement (2) combined
Similar reasoning as above can be applied using the same values for x, y, and z to show that it is NOT possible to determine with certainty whether there exists a value of i for which R is 0. Hence, Statement (1) and Statement (2) combined are insufficient.
E is the correct answer choice.
Additional DS Sample Questions:
Free GMAT DS prep (includes training videos and additional questions with explanations)
For Further Prep and Practice:
15 full-length GMAT practice tests (includes a free test)
End-to-end GMAT prep course online (includes 7-day free trial)
GMAT 5-weeks crash course
GMAT Prep + Admission Consulting Bundle






