Invest 30 seconds...
...for what may lead to a life altering association!
Help Line
- +91.8800.2828.00 (IND)
- 1030-1830 Hrs IST, Mon-Sat
- support@expertsglobal.com
...for what may lead to a life altering association!


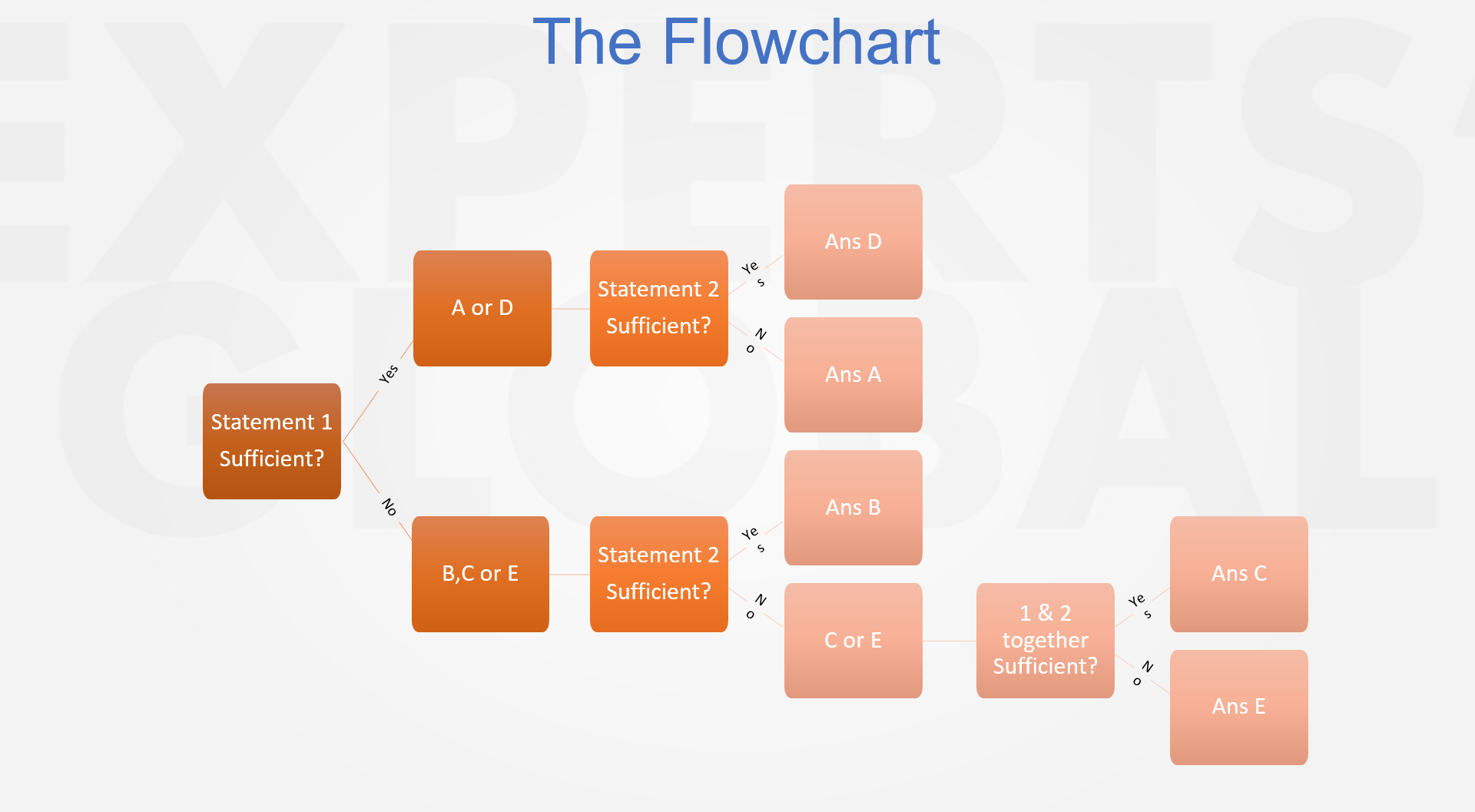
Data Sufficiency, often abbreviated as DS, is one of the most interesting and unusual elements on the GMAT. The structure is unlike what most students encounter in their regular academic work, which is why it feels unfamiliar at first. Instead of asking you to solve a problem outright, a DS question asks whether the information provided is sufficient to solve it. What the GMAT really checks here is not how quickly you calculate, but how calmly and clearly you judge sufficiency. Once you recognize the pattern, DS begins to feel less like a puzzle and more like a thoughtful game of logic. Out of the 20 questions in the Data Insights section of the GMAT, 5 to 7 are DS problems. Hence, thorough coverage of Data Sufficiency is a must in a dependable GMAT prep course.
On the GMAT Data Sufficiency questions, you do not need to arrive at an actual value; you simply need to judge how much information you have and whether the given statements are sufficient to answer the question. In principle, this should make these questions faster to solve and should lead to higher accuracy, since you are checking sufficiency rather than calculating a final value. However, for most GMAT candidates, accuracy on Data Sufficiency is actually a bit lower than on Problem Solving, and they often take longer to complete these questions. The main reason is the absence of a sound strategy. The following video lesson shares an organized and efficient approach: first look at Statement 1 alone and check if it is sufficient, then look at Statement 2 alone, independently, without combining it with Statement 1. You should combine the two statements only if each statement by itself fails to give you an answer. A statement is considered sufficient only when it leads to a unique and consistent answer. Once you understand this method well and practice it thoroughly, your accuracy on Data Sufficiency is likely to become higher than on other problem types, and you will take less time on average, because once again you are not required to compute a value, only to decide whether the statements are sufficient to answer the question. The following short video explains this approach, shows how it works, and prepares you to apply it across GMAT drills, sectional tests, and full length GMAT mocks.

Wish to know your current GMAT level? Take a free full-length GMAT diagnostic test
A statement on GMAT Data Sufficiency is treated as sufficient only when it leads to a unique and consistent answer to the given question. This answer may take one of three clear forms: a single, well defined numerical value, a consistent yes, or a consistent no, and in all of these cases the key idea is that the statement points to exactly one outcome that does not change across any valid interpretation. If, on the other hand, a statement allows for multiple numerical values, several different possibilities, or a maybe kind of outcome, then that statement is not considered sufficient, because any situation in which the result can vary or is not firmly pinned down to one answer fails the sufficiency test. The following video explains this idea in much greater detail and walks you through intuitive, real-life examples so that this definition of sufficiency becomes natural and easy to apply when you solve GMAT Data Sufficiency questions.

One of the first traps in Data Sufficiency is getting persuaded by answers that are not truly consistent. A statement is considered sufficient only when it yields the same outcome every single time, whether that outcome is a single definite number, a steady yes, or a steady no. If a statement can produce both yes and no, or if it supports more than one possible value, then it is insufficient. Many students unintentionally “support” the statement by picking examples that seem to prove sufficiency, while quietly overlooking counterexamples that reveal insufficiency. The real strength lies in actively trying to show that the statement is insufficient and seeing whether you can still break it. If every such attempt fails, then the statement is genuinely sufficient. The following video explains this trap through simple examples and guides you on how to navigate this trap on the GMAT.

One of the most frequent traps in Data Sufficiency is the habit of combining the two statements even when it is not needed. Many students believe that both statements must be used together to reach an answer, but that is far from the truth. The GMAT is checking not only your quantitative reasoning, but also your ability to isolate each piece of information and judge it on its own. The rule is straightforward: always evaluate each statement separately before you even consider combining them. If a single statement on its own leads to a clear yes or a clear no, that statement is sufficient, and remember that no is just as valid an answer as yes. When you combine statements too early, you are more likely to arrive at wrong answers and lose valuable time. This kind of clarity grows steadily with calm, focused practice. The following video explains this trap in detail through worked examples and also helps you navigate it on GMAT Data Sufficiency problems.

When working through GMAT Data Sufficiency questions, many students slip into a quiet trap: they assume that only a yes answer can make a statement sufficient. In truth, a no can also be a completely valid and sufficient answer, as long as it is firm and unambiguous. This is exactly where a clear, disciplined approach begins to set strong test takers apart from the rest. For instance, imagine a case where a statement clearly rules out a possibility and leaves no room for doubt. Even though the answer is no, that statement is still sufficient because it delivers a definite conclusion. Understanding this idea not only sharpens your accuracy but also stops you from wasting time by combining statements when it is not needed. The following video unpacks this trap through simple, concrete examples and shows you how to handle it on the GMAT.

In GMAT Data Sufficiency questions, some of the hardest traps hide inside very small details, and one of the most delicate and risky among them is the role of exceptions. Many students see a condition that looks decisive and assume that it will always lead to a yes answer, but a single missed case can change the sufficiency of a statement completely. Imagine a situation in which a statement seems to guarantee a positive result, yet one rare exception quietly breaks that confidence; if you miss that exception, you end up choosing the wrong option. This is where discipline, patience, and a careful eye matter deeply. Real strength in Data Sufficiency comes from resisting the urge to jump to conclusions and instead taking the time to test every possibility, including the hidden ones. The following video explores this trap in depth through worked examples and also helps you navigate it on GMAT Data Sufficiency problems.

One of the strongest lessons in GMAT Data Sufficiency is that when a question feels very easy, it often carries a hidden trap. The GMAT is built to measure your reasoning ability, not just how well you calculate. So, when you encounter a problem whose answer appears instantly obvious, it is important to pause and look at it again. Very often, something subtle yet critical is being overlooked. Consider, for instance, questions that involve the highest common factor of several integers. At first sight, the presence of a missing variable can make the statement appear insufficient, and many test takers reject it too quickly and choose the wrong option. In reality, specific relationships among the given numbers may already lock in the outcome, no matter what value the missing variable takes. The following video walks you through this trap using simple, clear examples.

Now that you have understood the approach for solving GMAT Data Sufficiency problems, as well as the main traps involved and the methods for navigating those traps on the GMAT, it is time to move to some real GMAT like questions for practice. The following video presents three simple looking Data Sufficiency problems that allow you to apply the strategies you have just learned and help you work through the very traps that were recently discussed. Although the underlying concept is very basic, namely even and odd integers, these problems introduce layers beneath their apparently straightforward surface. If you find yourself arriving at answers too quickly, there is a fair chance that you are overlooking something important. Please pause the video and attempt each problem on your own before watching the trainer solve them in a simple, efficient, and intuitive manner, in exactly the spirit in which you should approach such questions on the actual GMAT. Good luck solving these problems.

This section presents a collection of authentic GMAT-style Data Sufficiency questions, each accompanied by a thorough solution. Work through every item patiently and apply the reasoning process and concepts that you have just studied on this page for handling Data Sufficiency questions on the GMAT. At this stage, give priority to following the method carefully rather than merely arriving at the correct option. After you complete a question, use the explanation toggle to reveal the official-style answer and study the stepwise, descriptive solution.
Show Explanation
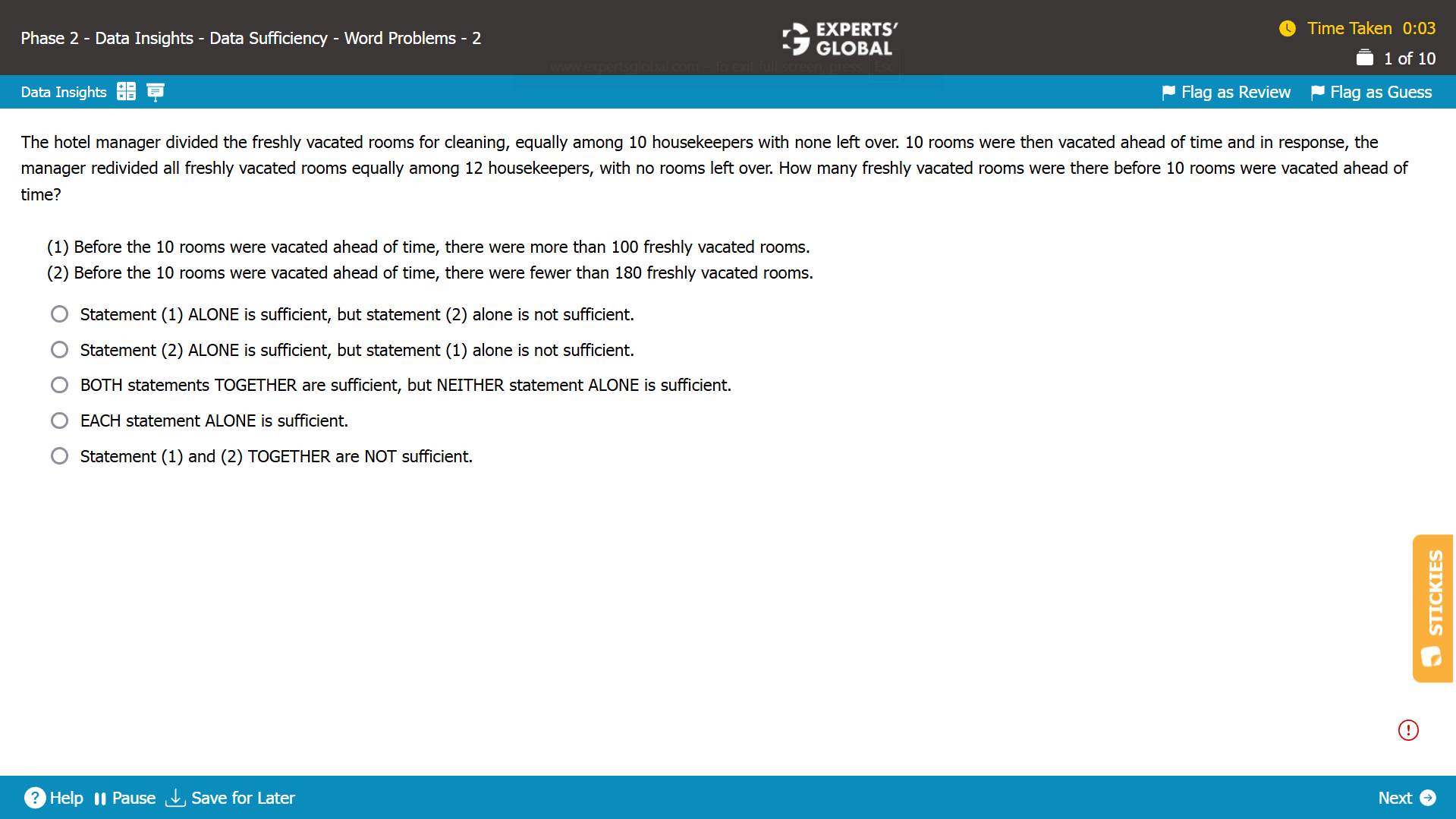
Let the initial number of vacated rooms be X.
Since the manager divided the rooms equally among 10 housekeepers with none left over: X is a multiple of 10.
The final number of vacated rooms after 10 more rooms were vacated = X + 10 Since the manager divided (X + 10) rooms equally among 12 housekeepers with none left over: (X + 10) is a multiple of 12.
We need to find whether the value of X can be determined.
Statement (1)
Since X > 100 and X is a multiple of 10, possible values of X are 110, 120, 130, 140, 150, 160, and so on.
However, since (X + 10) also needs to be a multiple of 12, the values of X that satisfy all the conditions are 110, 170, 230, and so on.
It is NOT possible to determine with certainty the value of X. Hence, Statement (1) is insufficient.
Statement (2)
Since X < 180 and X is a multiple of 10, possible values of X are 170, 160, 150, 140, 130, 120, 110, and so on.
However, since (X + 10) also needs to be a multiple of 12, the values of X that satisfy all the conditions are 170, 110, and 50.
It is NOT possible to determine with certainty the value of X. Hence, Statement (2) is insufficient.
As Statement (1) alone as well as Statement (2) alone is insufficient to answer the question, we need to now combine the two statements.
Statement (1) and Statement (2) combined
The two statements combined give us X = 110 and X = 170 as two solutions that satisfy all the conditions.
It is NOT possible to determine with certainty the value of X. Hence, Statement (1) and Statement (2) combined are insufficient.
E is the correct answer choice.
Show Explanation
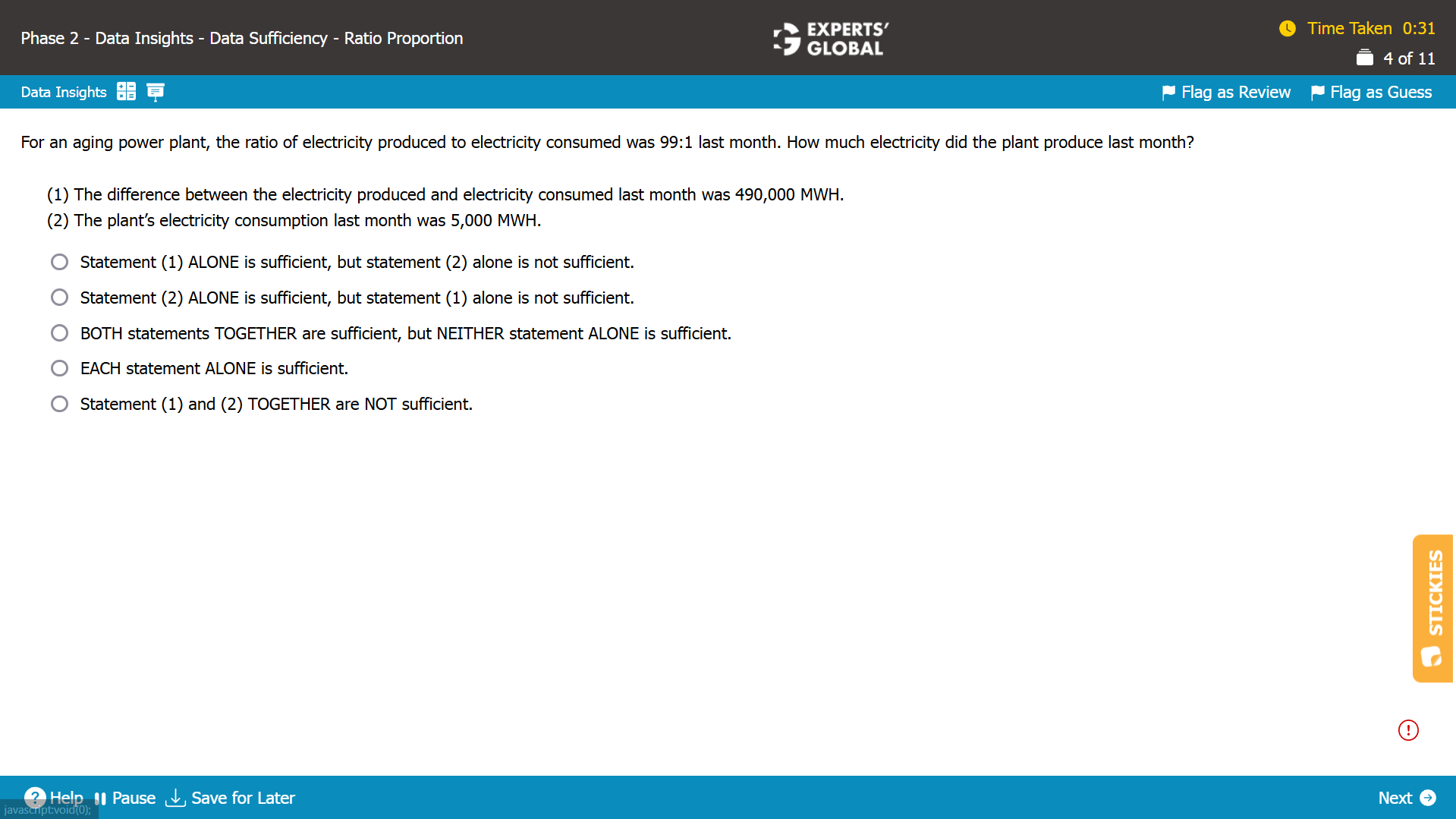
Let the amount of electricity produced last month be P.
Let the amount of electricity consumed last month be C.
Since the ratio of electricity produced to electricity consumed was 99:1, P/C = 99 (Equation I)
We need to find whether the value P can be determined.
Statement (1)
P – C = 490,000 (Equation II)
From Equation I and Equation II, we have 2 equations with 2 unknown variables that can be solved to determine the value of P. Hence, Statement (1) is sufficient.
Statement (2)
C = 5,000 (Equation III)
From Equation I and Equation III, we have 2 equations with 2 unknown variables that can be solved to determine the value of P. Hence, Statement (2) is sufficient.
D is the correct answer choice.
Show Explanation
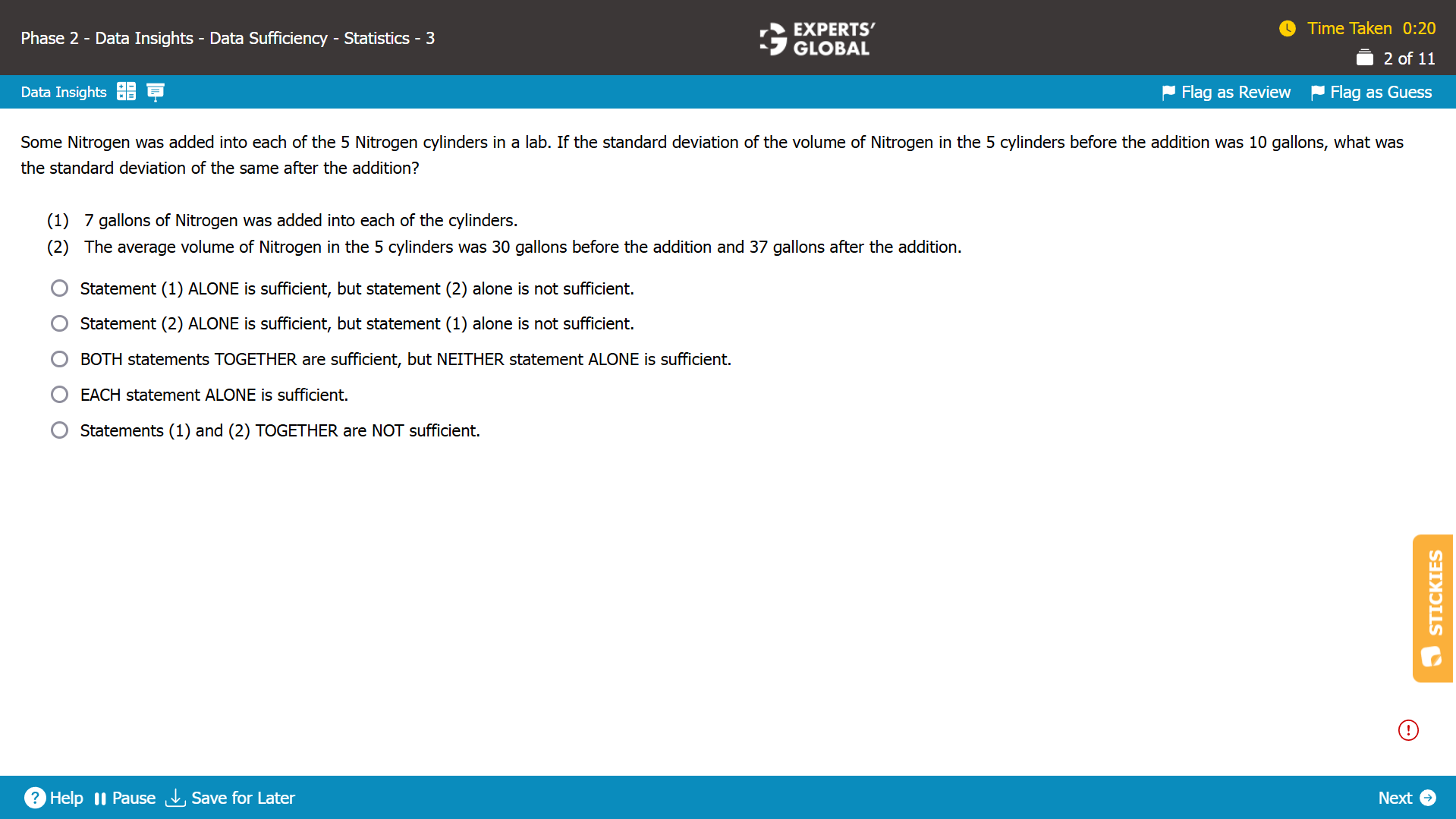
Show Explanation

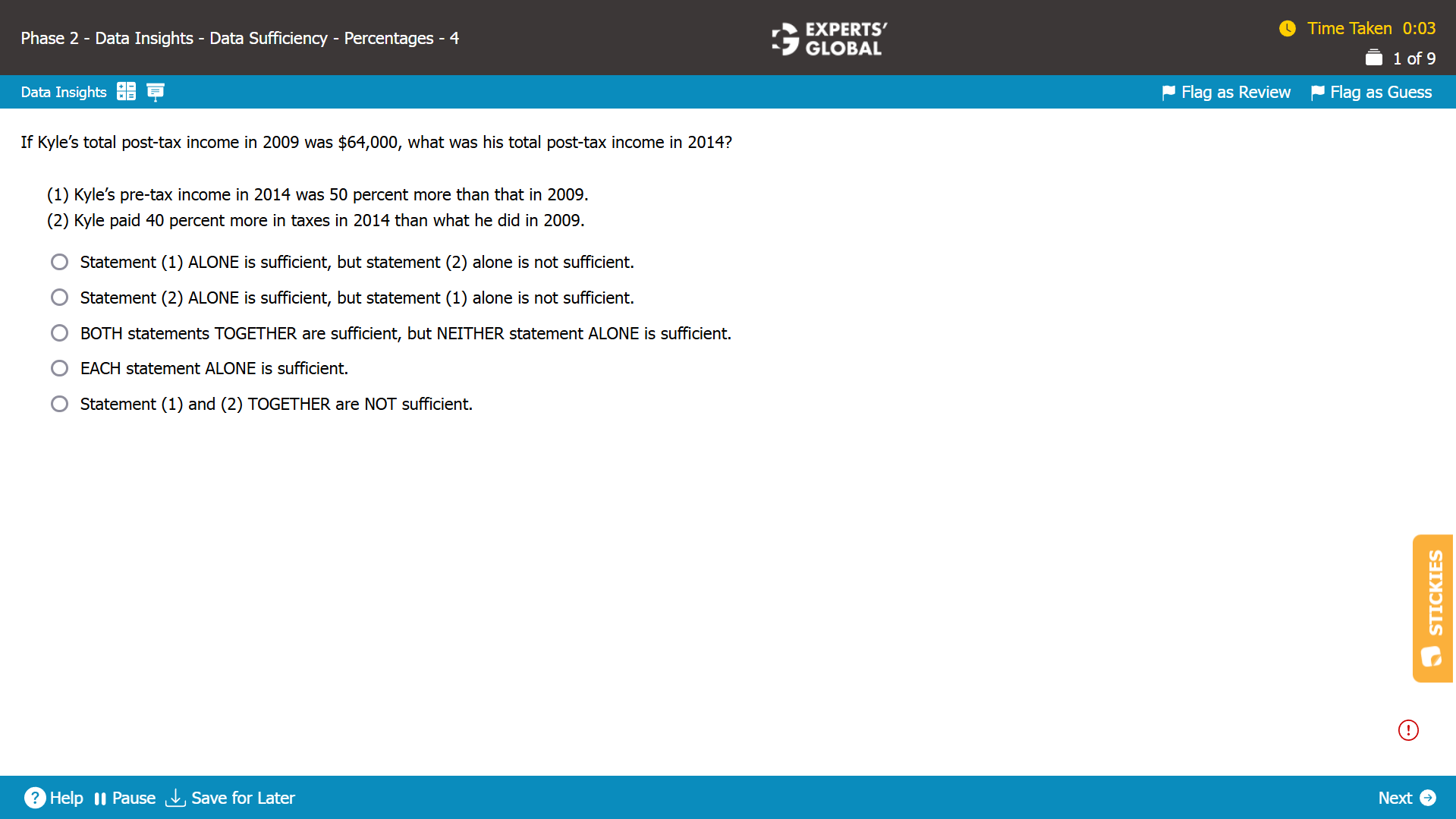
Written Explanation
Statement (1)
There are 5 nitrogen cylinders with a standard deviation of 10 gallons in their volume.
The standard deviation does not change when each element in a set is increased by the same absolute value.
So, if each cylinder is added with the same volume of 7 gallons, the standard deviation will not change and will remain to be 10 gallons. Sufficient.
Statement (2)
The average volume of 30 gallons before the addition indicates that the total volume in 5 cylinders was 30 X 5 = 150 gallons.
The average volume of 30 gallons after the addition indicates that the total volume in 5 cylinders is 37 X 5 = 185 gallons.
However, nothing is known about how much nitrogen was added to each cylinder. If an equal volume was added to each cylinder, the standard deviation could remain unchanged; on the other hand, if a different volume was added to each cylinder, the standard deviation will change.
Nothing can be determined about the standard deviation after the addition. Insufficient.
A is the correct answer choice.
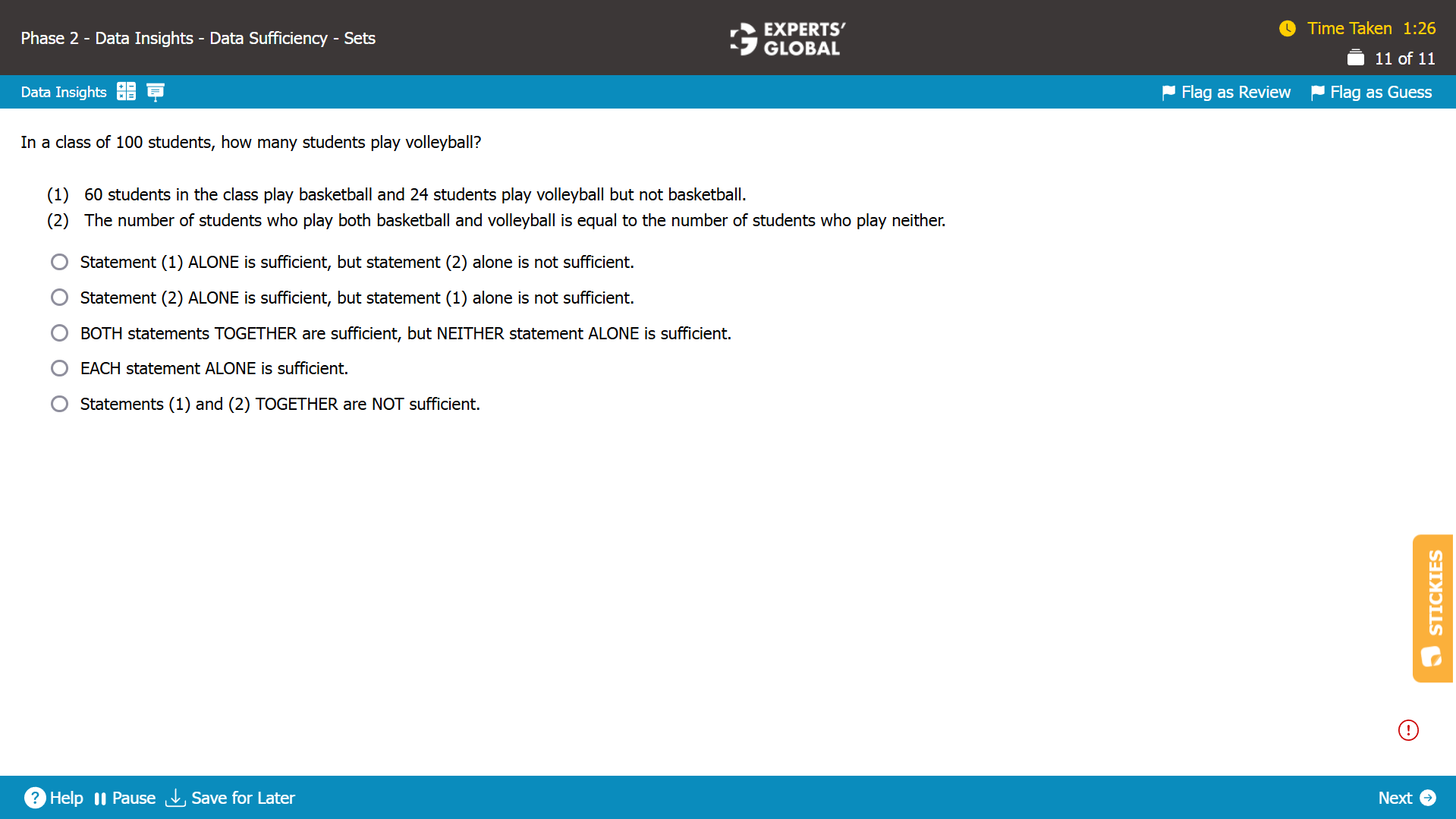
Show Explanation

Written Explanation
A + B + C + D = 100 students.
A + B needs to be determined.
Statement (1)
60 students play basketball.
B + C = 60.
24 students play volleyball but not basketball.
A = 24.
No information about B can be derived. The number of students who play volleyball cannot be determined. Insufficient.
Statement (2)
The number of students who play both basketball and volleyball is equal to the number of students who play neither
So, B = D.
No information about A can be derived. No information about the absolute value of B can be derived. The number of students who play volleyball cannot be determined. Insufficient.
Because both the statements alone are not sufficient, let’s combine the two statements.
Statement (1) and Statement (2) combined
60 students play basketball.
B + C = 60.
24 students play volleyball but not basketball.
A = 24.
Additionally, the number of students who play both basketball and volleyball is equal to the number of students who play neither
So, B = D.
A + (B + C) + D = 100
24 + (60) + D = 100
D = 16.
B = 16.
A + B = 24 + 16 = 40 students.
The number of students who play volleyball can be determined. Sufficient.
C is the correct answer choice.
High quality Data Sufficiency questions are not available in large numbers. Among the limited, genuinely strong sources are the official practice materials is released by GMAC and the Experts’ Global GMAT course. Within the Experts’ Global GMAT online preparation course, every Data Sufficiency problem appears on an exact GMAT like user interface that includes all the real exam tools and features. You work through more than 200 Data Sufficiency questions in quizzes and also take 15 full-length GMAT mock tests that include several Data Sufficiency questions in roughly the same spread and proportion in which they appear on the actual GMAT.
All the best!