Invest 30 seconds...
...for what may lead to a life altering association!
Help Line
- +91.8800.2828.00 (IND)
- 1030-1830 Hrs IST, Mon-Sat
- support@expertsglobal.com
...for what may lead to a life altering association!


Linear equations (or simple equations) describe relationships where the variables change at a constant rate, while quadratic equations describe relationships where the variables change in a squared or curved pattern. Together, they form a core part of algebra and support many problem solving situations on the test. Careful attention to these concepts is an essential part of any comprehensive GMAT preparation course. This page offers you an organized subtopic wise playlist, along with a few worked examples, for efficient preparation of this concept.
One of the most powerful time saving habits on the GMAT is knowing when to cut down the number of variables in a question. Many students automatically bring in several unknowns for simple relationships, which only stretches the work and increases the chance of slips. A neater, faster method is to express everything in terms of a single variable whenever you can. This approach not only lightens the calculations but also reduces confusion and keeps the solution well organized. For instance, in questions about salaries, investments, or proportions, you can treat the total as one variable and write all other parts as fractions of that total. This way, the entire problem collapses into a clean equation, often solvable in just one step. The video below explains this approach step by step, shows how it works in practice, and prepares you for GMAT drills, sectional tests, and full-length GMAT mock tests.

Quadratic equations become surprisingly graceful once you start seeing their underlying pattern, and they are quite manageable when you bring the right approach to them. On the GMAT, they are used to check how well you can recognize structure and dismantle a problem efficiently. One of the most dependable techniques for solving quadratic equations is factorization, where you split the middle term into two parts whose product matches the product of the first and last coefficients. The following short video explains this concept gently and demonstrates how it might appear on the GMAT. This brief video offers a clear explanation of the concept and shows how it may be tested on the GMAT.

On this page, you will work through a selected set of GMAT-style Linear and Quadratic Equations questions, each supported by a complete, stepwise explanation. Move through every problem at a measured pace and rely on the methods and ideas you have just studied here for solving linear and quadratic equations on the GMAT. At this stage, focus more on applying the structured approach accurately than on simply obtaining the right answer. After you finish each question, open the explanation panel to verify the correct option and to review the reasoning in detail.
Show Explanation

Written Explanation
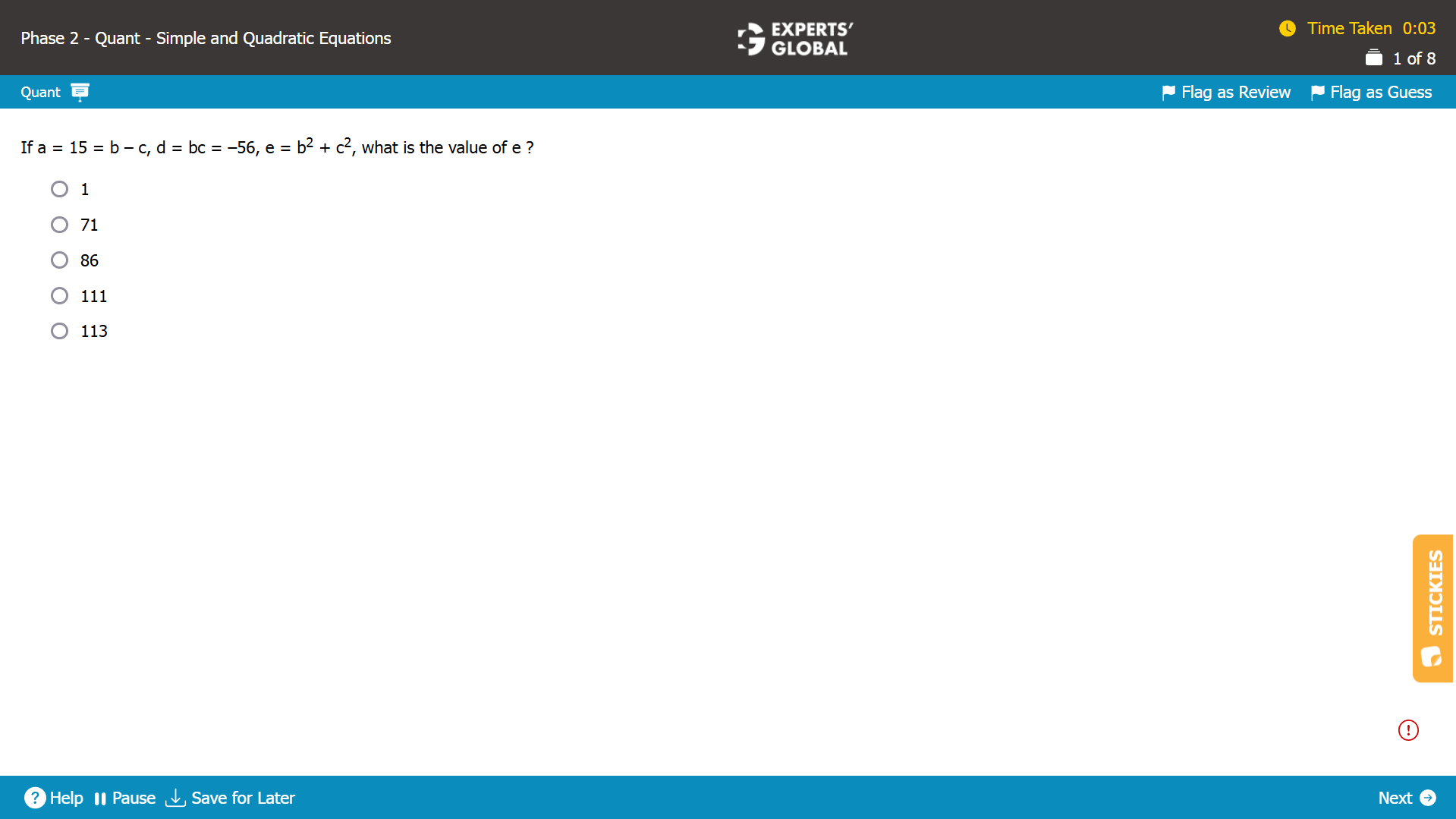
b – c = 15
bc = –56
(b – c)2 = b2 + c2 – 2bc.
So, b2 + c2 = (b – c)2 + 2bc.
Hence, e = b2 + c2 = (b – c)2 + 2bc = 152 + 2 X (–56) = 225 – 112 = 113.
E is the correct answer choice.
Show Explanation

Written Explanation
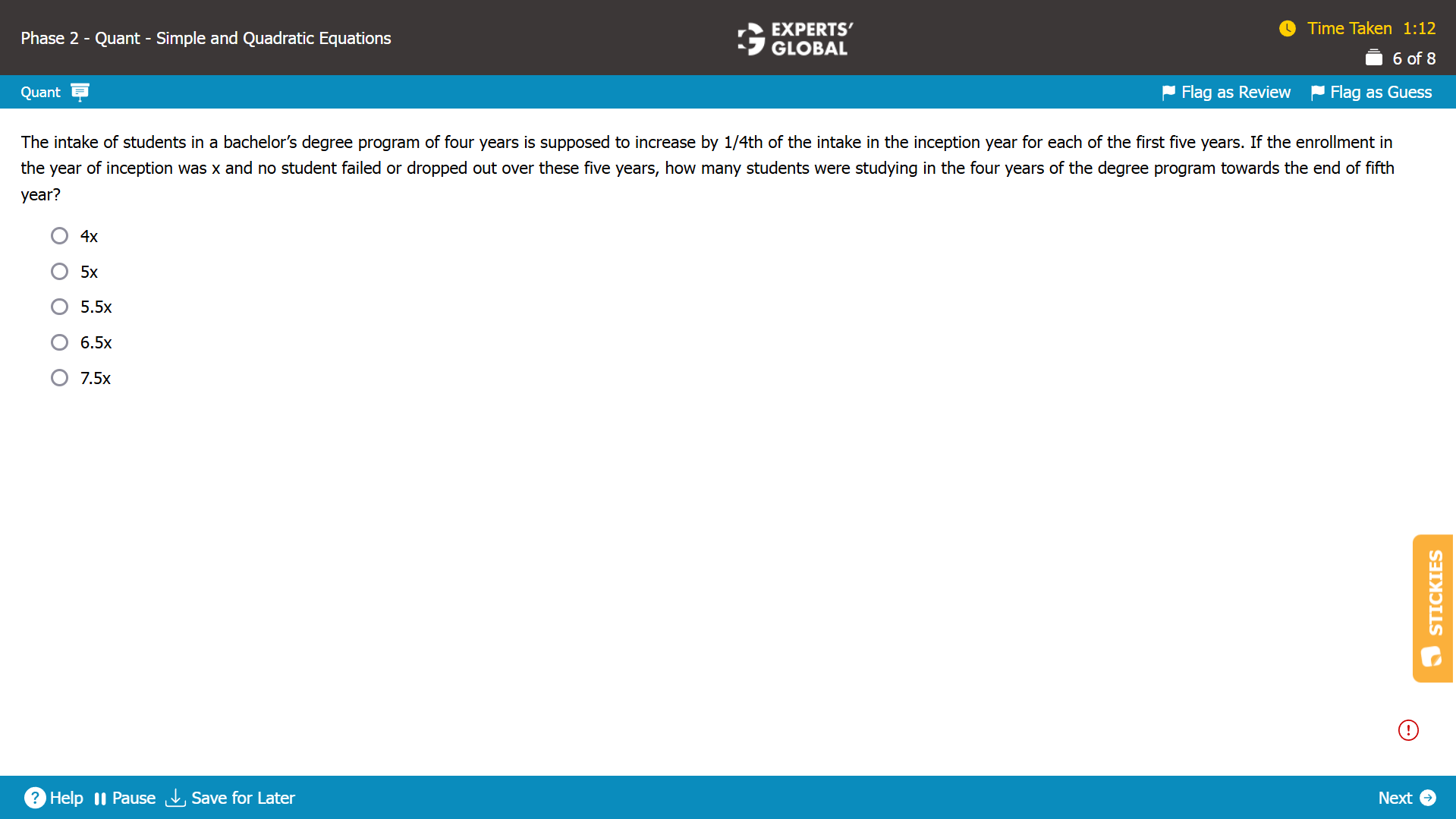
Year 1
Let’s say the first year enrollment was x.
Total number of students in this year = x.
Year 2:
x students go to the second year of college.
1.25x students enter the first year of college.
Total number of students in this year = x + 1.25x.
Year 3:
x students go to the third year of college.
1.25x students enter the second year of college.
1.5x students enter the first year of college.
Total number of students in this year = x + 1.25x + 1.5x.
Year 4:
x students go to the fourth year of college.
1.25x students enter the third year of college.
1.5x students enter the second year of college.
1.75x students enter the first year of college.
Total number of students in this year = x + 1.25x + 1.5 x + 1.75x.
Year 5:
x students graduate from the college.
1.25x students enter the fourth year of college.
1.5x students enter the third year of college.
1.75x students enter the second year of college.
2x students enter the first year of college.
Total number of students in this year = 1.25x + 1.5 x + 1.75x + 2x = 6.5x.
D is the correct answer choice.
Show Explanation

Written Explanation
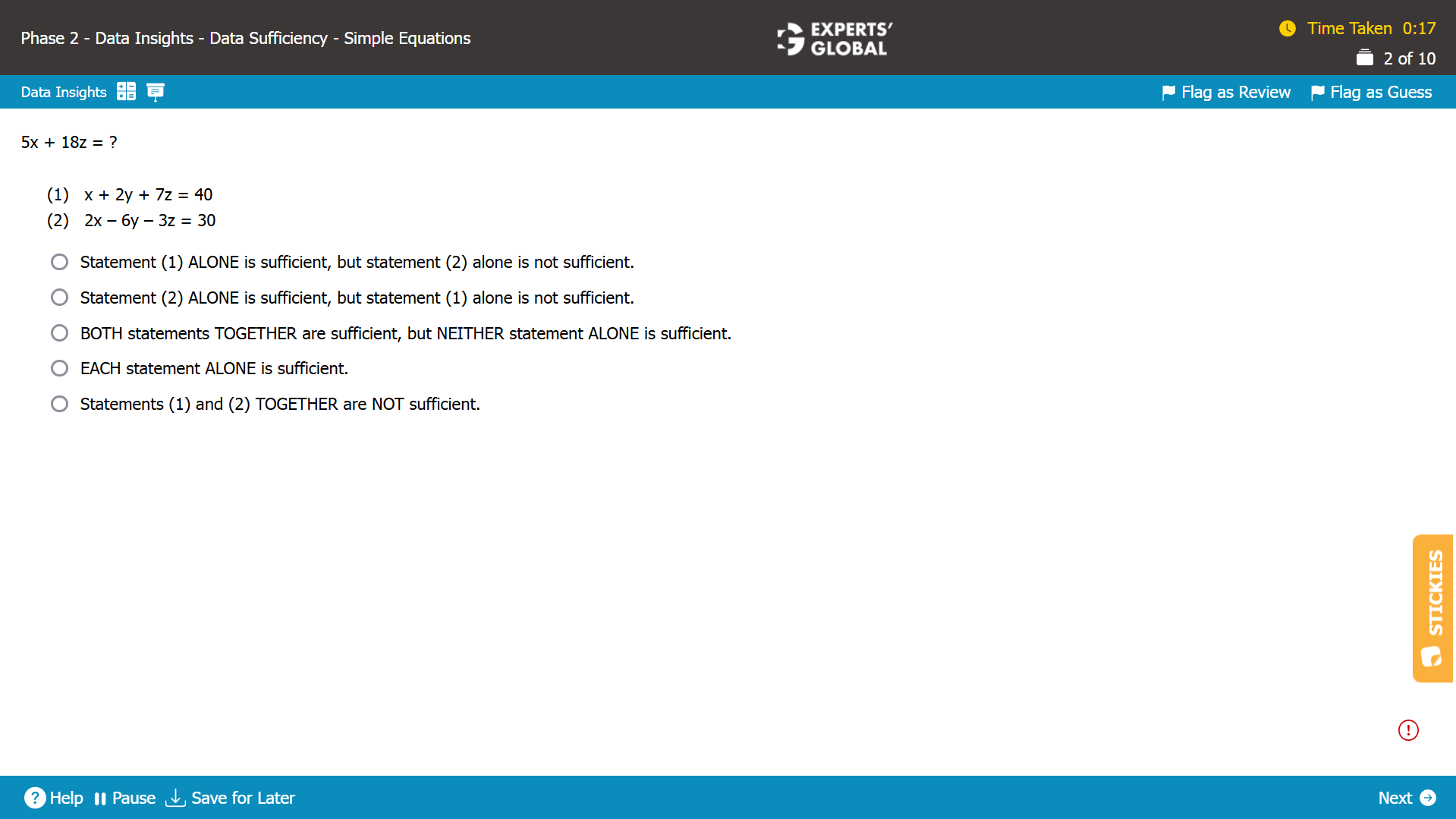
Statement (1)
x + 2y + 7z = 40
This is one equation with three variables. One variable cannot be eliminated to derive an expression in the other two variables.
5x + 18z cannot be determined. Insufficient.
Statement (2)
2x – 6y – 3z = 30
This is one equation with three variables. One variable cannot be eliminated to derive an expression in the other two variables.
5x + 18z cannot be determined. Insufficient.
Because both the statements alone are not sufficient, let’s combine the two statements.
Statement (1) and Statement (2) combined
x + 2y + 7z = 40
So, 3x + 6y + 21z = 120
2x – 6y – 3z = 30
There are two equations with three variables. One variable can be eliminated to derive an expression in the other two variables.
Adding the two equations…
(3x + 2x) + (6y – 6y) + (21z – 3z) = 120 + 30
5x + 18z = 150
5x + 18z can be determined. Sufficient.
C is the correct answer choice.
Show Explanation

Written Explanation
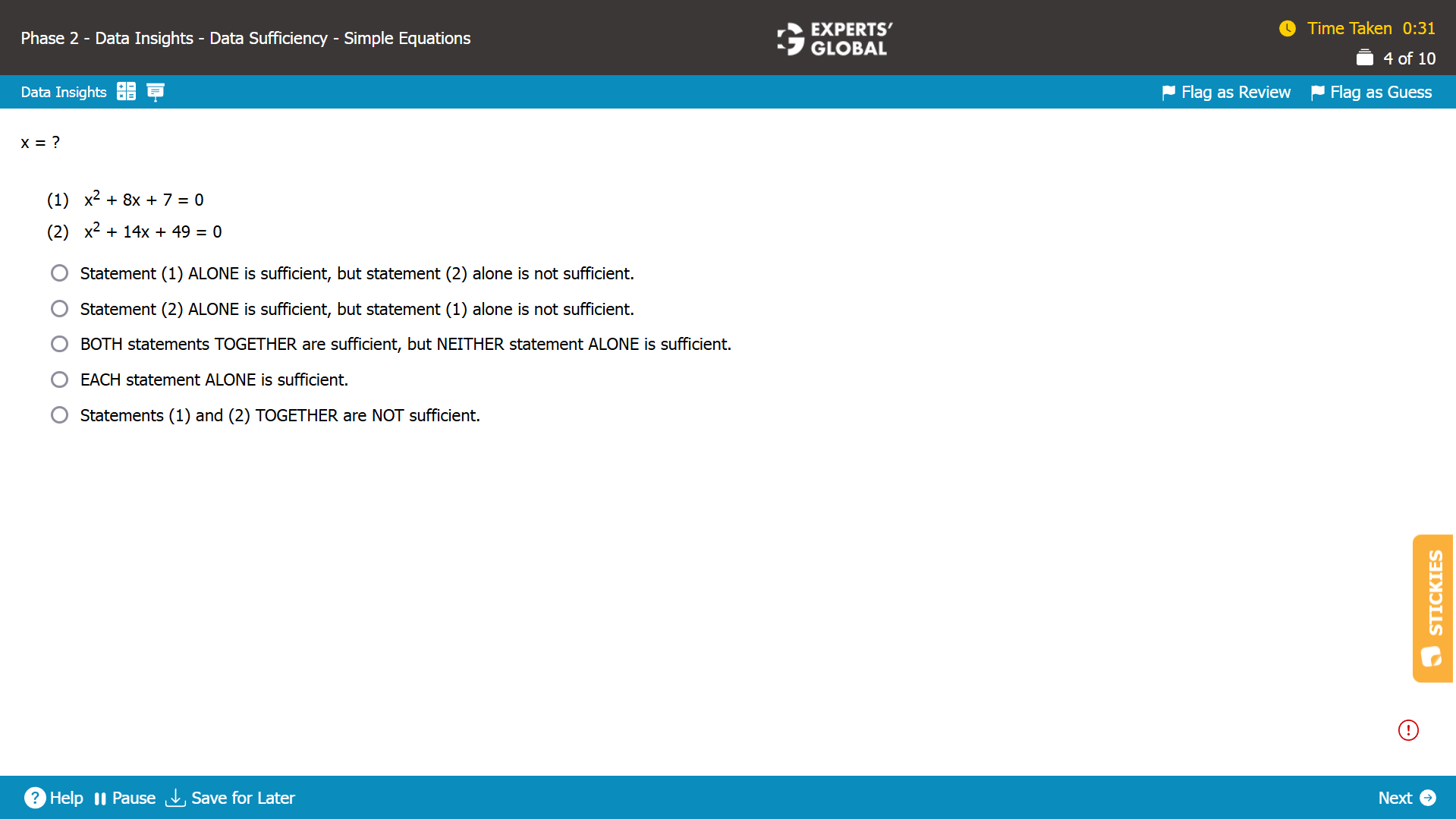
Statement (1)
x2 + 8x + 7 = 0
This is a quadratic equation with 2 roots. Please note that the exact answer is not required to be calculated in a Data Sufficiency question.
So, there will be two values of x. Insufficient.
Statement (2)
x2 – 14x + 49 = 0
A quadratic equation has 2 roots; but (x2 – 14x + 49) is the perfect square of (x – 7). So, this equation will have only one root. Sufficient.
B is the correct answer choice.
Show Explanation

Written Explanation
Statement (1)
x2 – 7x + 12 = 0
(x – 4) (x – 3) = 0
x = 4 or x = 3
Whether x = 4 cannot be determined. Insufficient.
Statement (2)
x2 – 4x + 3 = 0
(x – 3) (x – 1) = 0
x = 3 or x = 1
Neither of the roots is 4; so, x cannot be 4. Sufficient.
B is the correct answer choice.
High quality Linear and Quadratic Equations questions are not available in large numbers. Among the limited, genuinely strong sources are the official practice materials released by GMAC and the Experts’ Global GMAT course. Within the Experts’ Global GMAT online preparation course, every Linear and Quadratic Equations problem appears on an exact GMAT like user interface that includes all the real exam tools and features. You work through more than 100 Linear and Quadratic Equations questions in quizzes and also take 15 full-length GMAT mock tests that include several Linear and Quadratic Equations questions in roughly the same spread and proportion in which they appear on the actual GMAT.