Overlapping sets problems involve situations where people or objects belong to more than one group at the same time, and the goal is to understand how these groups combine or intersect. These questions require you to organize information clearly and reason through counts with care. Mastering this idea is an essential part of any end-to-end GMAT preparation course. This page offers you an organized subtopic wise playlist, along with a few GMAT-style worked examples, for efficient preparation of this concept.
Venn Diagram: Two Overlapping Sets
Venn diagrams are among the simplest and yet most powerful tools for handling set based questions on the GMAT. The central idea is to arrange the information in a clear layout so that nothing is overlooked and every part of the set is shown. When there are only two sets, say A and B, the totals for each set are best written outside the circles. The common region between the circles becomes the key focus, because it shows the items that belong to both sets. The area outside both circles represents those who belong to neither. The non overlapping sections of the two circles stand for “A but not B” (only A) and “B but not A” (only B) respectively. Once you put this structure in place, you can handle every follow up question with confidence. This approach keeps you from getting lost in the wording and allows you to depend on a neat visual picture instead. The following short video explains and demonstrates this approach, then prepares you to use it across GMAT drills, sectional tests, and the full length GMAT mock tests.
Venn Diagram: Two Overlapping Sets
Key Slide Recap
Venn Diagram: Three Overlapping Sets
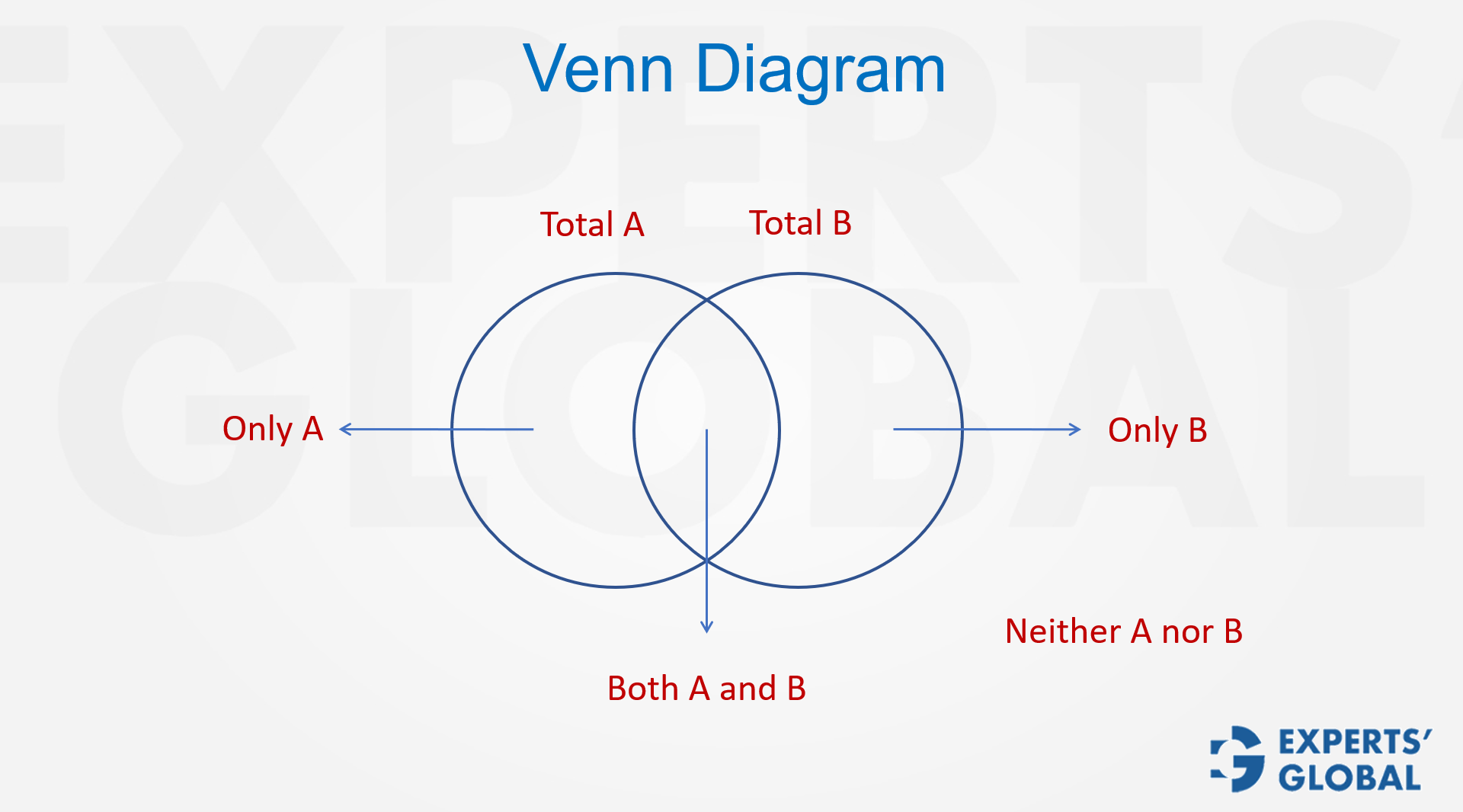
When a problem involves three sets, the situation becomes rich and engaging. Numbers can intersect in surprising ways, and if you do not organize the information carefully, mistakes slip in easily. A neat three circle Venn diagram is the most effective way to manage such cases. Begin by writing the totals outside each circle, then gently place the overlapping values, starting with the most important part: the region that belongs to all three sets at once. Once that central area is fixed, everything else starts to settle into place. Each remaining section, whether it represents pairs of sets, single sets, or the area outside, can then be filled in a calm, logical order. With the diagram complete, all follow up questions become straightforward. Instead of juggling numbers in your mind, you lean on a clear visual framework that keeps every detail safely in view. The brief video that follows explains this idea through simple reasoning and shows how it may be tested on the GMAT.
Venn Diagram: Three Overlapping Sets
Key Slide Recap
Wish to know your current GMAT level? Register for a free full-length diagnostic GMAT test
Line Diagram for Solving Overlapping Sets
A line diagram is a simple number line that shows how ranges overlap, separate, or combine, making it an excellent tool for solving GMAT Problem Solving questions on overlapping sets. It turns complex verbal descriptions into a clear visual layout, helps you mark boundaries with precision, and lets you read each segment as a share of the whole. In the conceptual video below, you will see how line diagrams are built step by step on overlapping set problems, so that you can apply this tool efficiently and calmly under exam time pressure.
Line Diagram for Solving Overlapping Sets
Key Slide Recap
Venn Diagram vs Line Diagram for Overlapping Sets
The choice between a Venn diagram and a line diagram becomes much easier once you understand the type of information each is built to hold. A Venn diagram is a natural fit when the data is divided into categories or types, such as people belonging to different clubs or products falling into different segments. A line diagram is more suitable when the information sits on a numerical range, such as scores, ages, or time intervals that partially overlap. In the conceptual video below, you will see clear examples of both tools on overlapping set problems, so you can decide quickly which diagram to use and solve GMAT questions efficiently and calmly in the exam setting.
Venn Diagram vs Line Diagram for Overlapping Sets
Key Slide Recap
GMAT-style Overlapping Sets Questions with Explanations
This section offers a collection of GMAT-style Overlapping Sets questions, each paired with a careful, fully worked explanation. Move through every question at a measured pace and use the frameworks and ideas that you have just studied on this page for approaching Overlapping Sets questions on the GMAT. At this stage, place more emphasis on applying the structured method consistently than on simply choosing the right option. After you complete each question, use the explanation toggle to reveal the correct answer and review the reasoning in detail.
GMAT Overlapping Sets Practice Question 1
Written Explanation
75% students passed In Biology.
So, A + B = 75… (Equation I)
20% students failed in Chemistry. So, 100 – 20 = 80% students passed in Chemistry.
So, B + C = 80… (Equation II)
75% of those who passed in Chemistry also passed in Biology.
So, (75 / 100) X (B + C) = B
3B + 3C = 4B
B = 3C
Substituting this value in Equation II…
3C + C = 80
So, C = 20%.
Substituting this value in Equation II…
20 + B = 80
So, B = 60%.
Substituting this value in Equation I…
A + 60 = 75
So, A = 15%.
Percentage of students passing at least one subject = A + B + C = 15 + 60 + 20 = 95%.
Total number of students = 120.
So, number of students passing at least one subject = 120 X (95 / 100) = 114.
114 students passed at least one subject.
E is the correct answer choice.
GMAT Overlapping Sets Practice Question 2
Written Explanation
When three sets intersect…
(Set 1 population + Set 2 population + Set 3 population) – (the population common in at least two sets) – (the population common in all the three sets) = total population in at least one set
This can be verified from the above diagram as follows.
((A + E + G + D) + (B + E + F + D) + (C + G + F + D)) – (E + D + F + D + G + D) – D = A + B + C + E + F + G +D.
So,
(Yoga residents + cycling residents + morning walk residents) – (residents who engage in two or more of these three activities) – (residents who engage in all three activities) = Number of residents who engage in at least one activity
Residents practice yoga = 40%
Residents going for cycling = 50%
Residents going for morning walk = 60%
Residents who engage in two or more of these three activities = 65%
Residents who engage in all three activities = 10%
Overall,
(40 + 50 + 60) – (65) – (10) = 75% of residents engage in at least one activity.
So, 100 – 75 = 25% of the residents engage in none of the three activities.
[Alternatively…
40% of residents practice yoga.
So, A + E + D + G = 40%.
50% of residents go for cycling.
So, B + F + D + E = 50%.
60% residents go for morning walk.
So, C + G + D + F = 60%.
65% of the total residents engage in two or more of these three activities.
So, G + E + F + D = 65% … (Equation I)
Adding all of the equations…
(A + E + D + G) + (B + F + D + E) + (C + G + D + F) + (G + E + F + D) = 40 + 50 + 60 + 65
A + B + C + 3E + 3F + 3G + 4D = 215% … (Equation II)
10% residents engage in all the three activities.
So, D = 10%
Substituting D = 10 in Equation II…
A + B + C + 3E + 3F + 3G + 4 X 10 = 215
A + B + C + 3 (E + F + G) = 175% … (Equation III)
Substituting D = 10 in Equation I…
E + F + G = 65 – 10 = 55%
Substituting this value in Equation III…
A + B + C + 3 (55) = 175
A + B + C = 10%.
Overall…
The percentage of residents who engage in at least one of the three activities = (A + B + C) + (E + F + G) + D = 10 + 55 + 10 = 75%.
The percentage of residents who engage in none of the three activities = 100% – 75% = 25%.
25% of the residents engage in none of the three activities.]
D is the correct answer choice.
GMAT Overlapping Sets Practice Question 3
Written Explanation
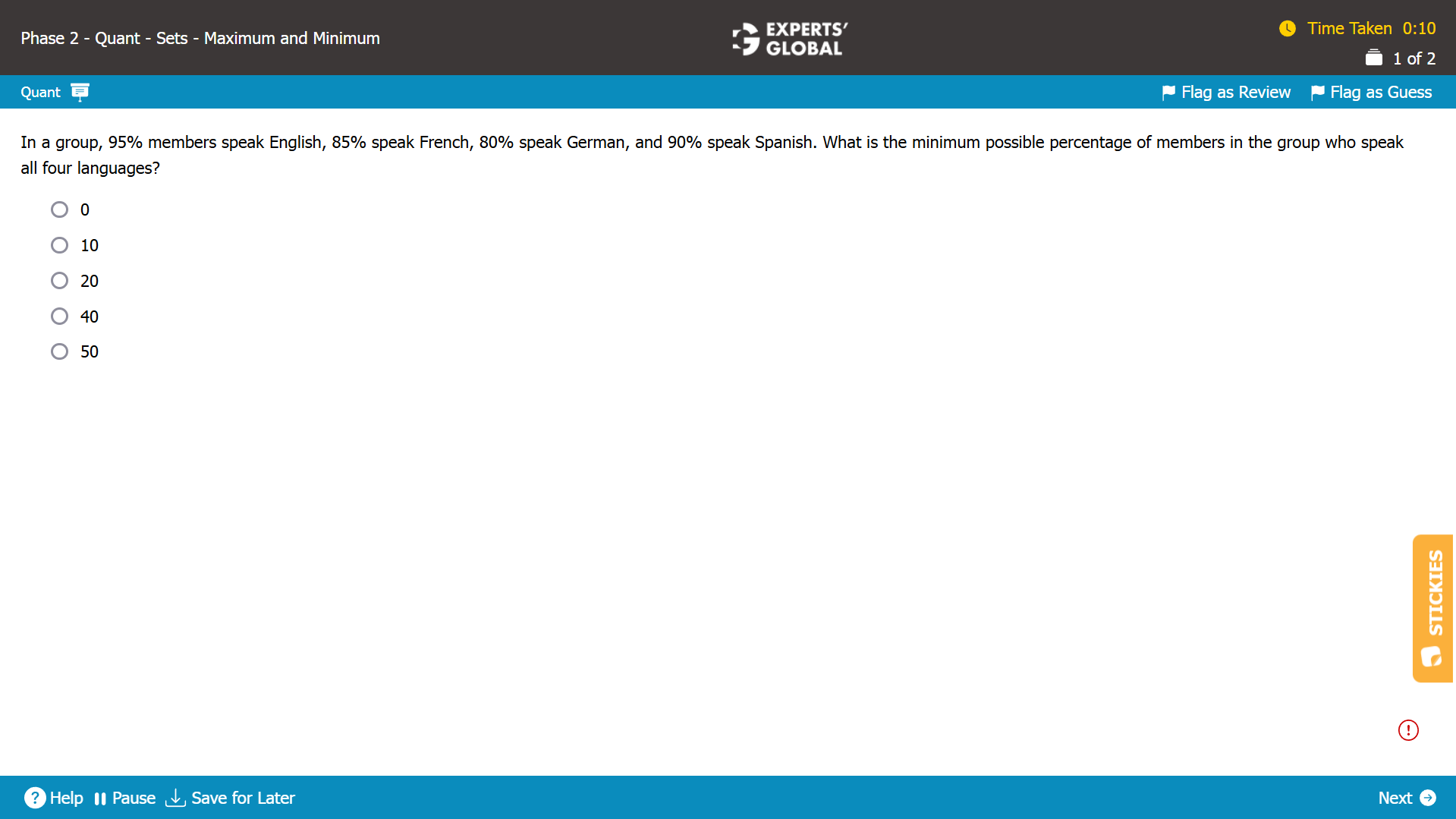
To find the minimum possible percentage who speak all four languages, let’s say that NO ONE wants to speak the fourth language and everyone wants to speak only three languages.
If everyone speaks all three languages, there can be 3 X 100% = 300% persons accounted for.
However, we need to account for 95% + 85% + 80% + 90% = 350% of persons.
So, 350% – 300% = 50% person must speak the fourth language.
In other words, a minimum of 50% must speak all four languages.
E is the correct answer choice.
GMAT Overlapping Sets Practice Question 4
Written Explanation
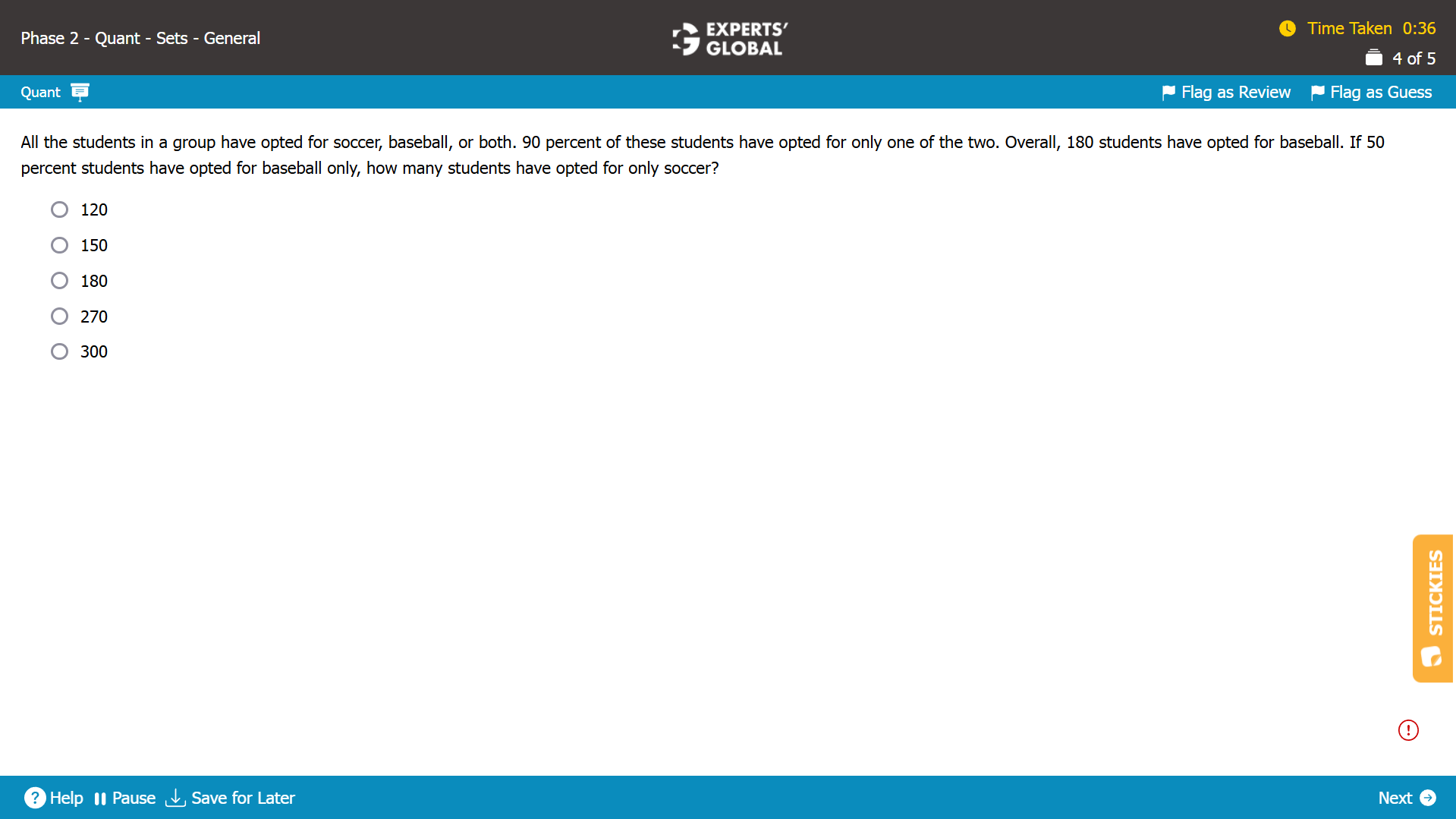
90% of students have opted for only one sport.
So, A + C = 90% … (Equation I)
180 students have opted for baseball.
So, B + C = 180 … (Equation II)
50% of students have opted for baseball only.
C = 50%.
Substituting the value of C in Equation I…
A = 90 – 50 = 40%.
A + B + C = 100%
So, 40 + B + 50 = 100
B = 10%.
B + C = 10 + 50 = 60%.
Substituting this value in Equation II….
180 = 60% of all students.
Total number of students = (180 / 60) X 100 = 300.
Number of students who have opted for only soccer = A = 40% of all students = 40 X 300 = 120.
So, 120 students have opted for only soccer.
A is the correct answer choice.
GMAT Overlapping Sets Practice Question 5
Written Explanation
When three sets intersect…
(Set 1 population + Set 2 population + Set 3 population) – (the population common in two sets) + (the population common in all the three sets) + (the population in no set) = Total population
This can be verified from the above diagram as follows.
((A + E + G + D) + (B + E + F + D) + (C + G + F + D)) – (E + D + F + D + G + D) + D + H = A + B + C + E + F + G +D + H
So,
(Pizza members + burger members + salad members) – (members who like two of these items) + (members who like all three items) + (members who like none of the three items) = Total number of members
Pizza members = 50
Burger members = 70
Salad members = 45
So, Pizza members + burger members + salad members = 50 + 70 + 45 = 165.
Pizza and burger members = 25
Burger and salad members = 30
Pizza and salad members = 20
Members who like two of these items = 25 + 30 + 20 = 75.
Members who like all three items = Pizza, burger, and salad members = 10.
Members who like none of the three items = 5.
Overall,
(Pizza members + burger members + salad members) – (members who like two of these items) + (members who like all three items) + (members who like none of the three items) = Total number of members
(165) – (75) + (10) + (5) = Total number of members
Total number of members = 105.
There are 105 total members of the club.
B is the correct answer choice.
GMAT Overlapping Sets Practice Question 6
Written Explanation
When three sets intersect…
(The population common in two sets) – 3 X (the population common in all the three sets) = (the population common in exactly two sets)
This can be verified from the above diagram as follows.
(E + D + F + D + G + D) – 3D = E + F + G
So,
Speakers of exactly two of these languages = speakers of two of these languages – 3 X (speakers of all three languages)
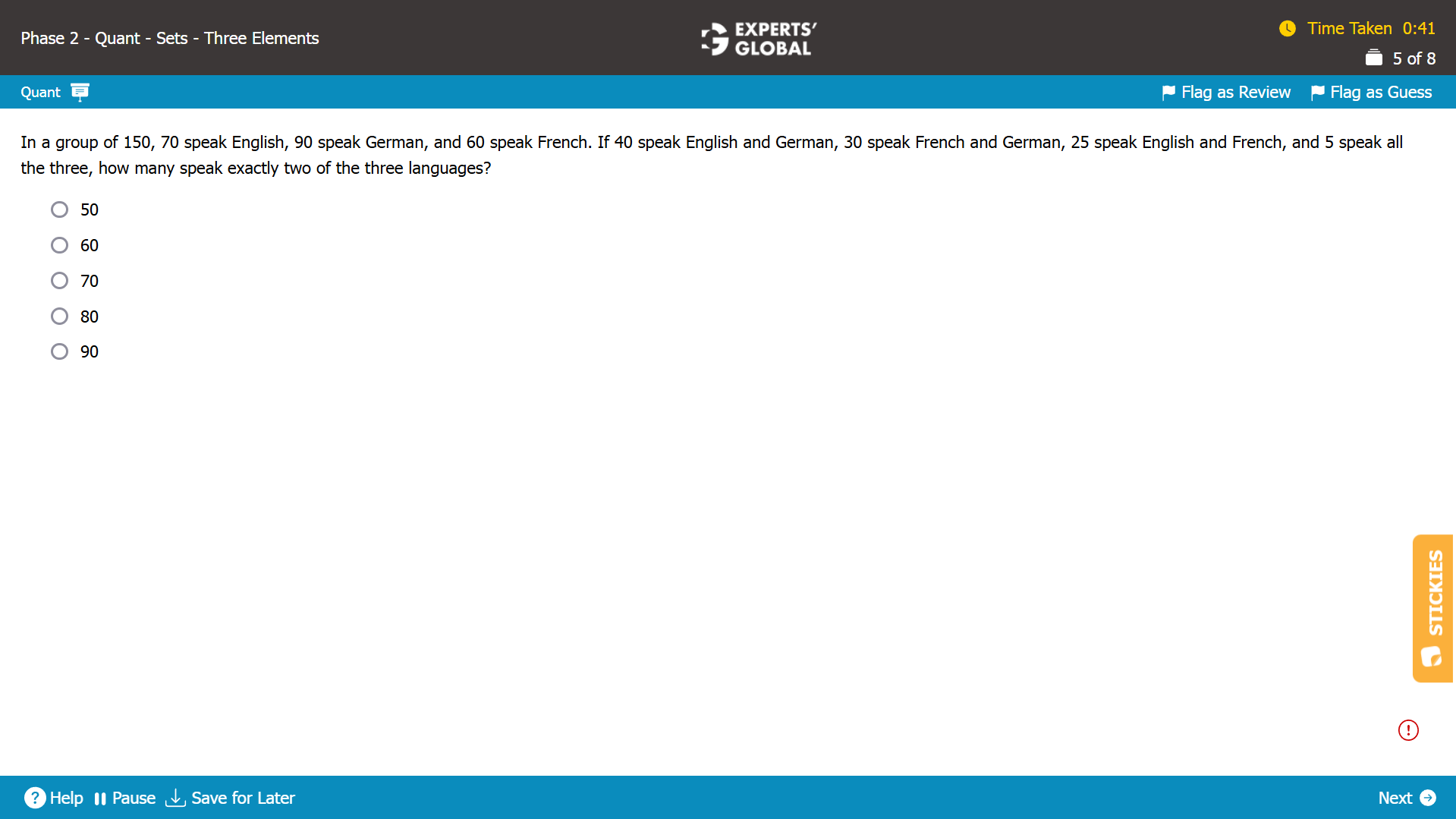
English and German speakers = 40
French and German speakers = 30
English and French speakers = 25
Speakers of two of these languages = 40 + 30 + 25 = 95.
Speakers of all three languages = 5.
So. speakers of exactly two of these languages = 95 – 3(5) = 80.
80 people speak exactly two of the three languages.
D is the correct answer choice.
GMAT Overlapping Sets Practice Question 7
Written Explanation
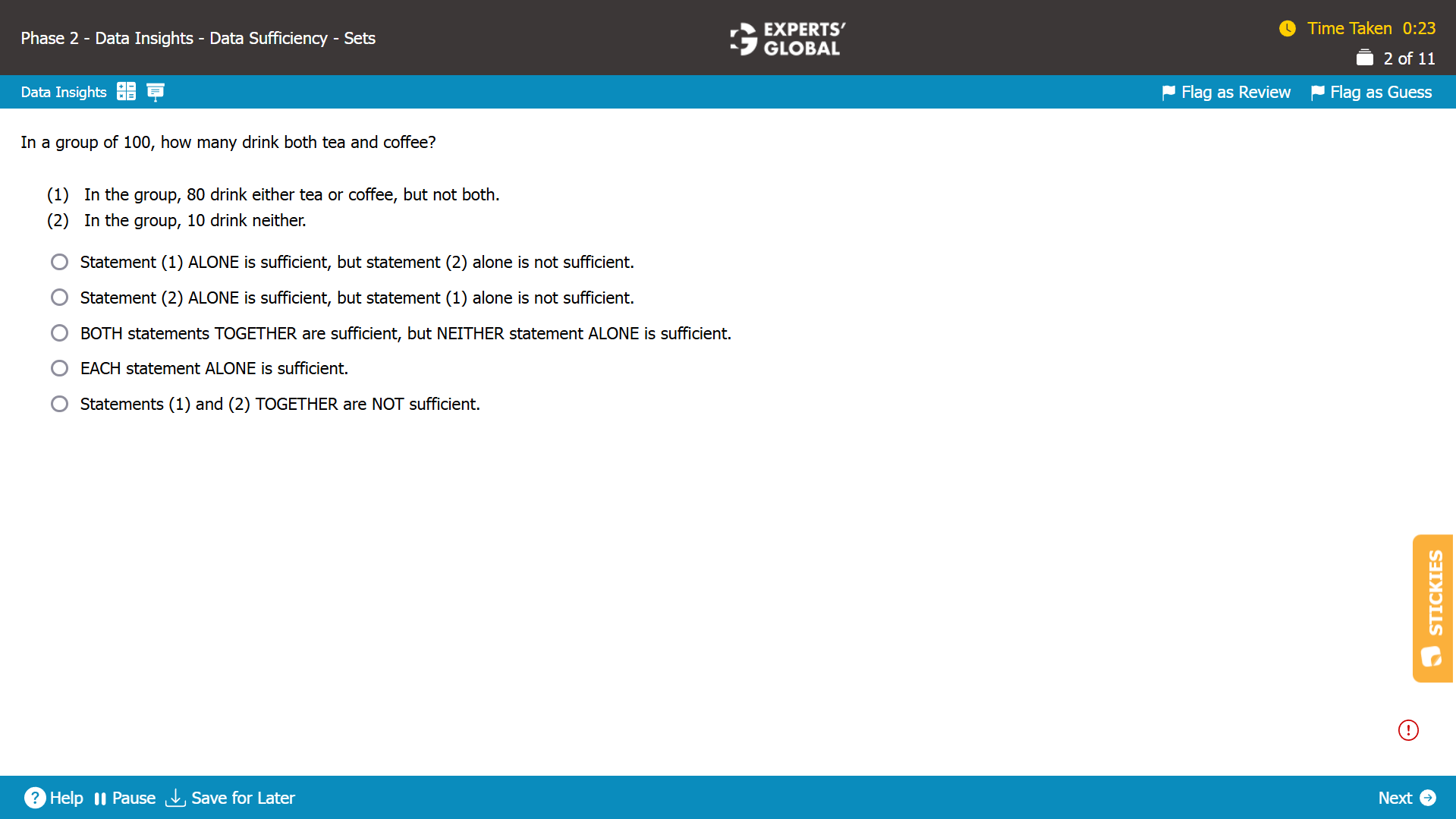
A + B + C + D = 100.
Statement (1)
80 members drink either tea or coffee, but not both.
A + C = 80.
A + B + C + D = 100.
So, B + D = (A + B + C + D) – (A + C) = 100 – 80 = 20.
Nothing is known about D. So, B cannot be determined.
How many members drink both tea and coffee cannot be determined. Insufficient.
Statement (2)
In the group, 10 drink neither.
D = 10.
A + B + C + D = 100.
So, A+ B + C = (A + B + C + D) – (D) = 100 – 10 = 90.
Nothing is known about A and C. So, B cannot be determined.
How many members drink both tea and coffee cannot be determined. Insufficient.
Because both the statements alone are not sufficient, let’s combine the two statements.
Statement (1) and Statement (2) combined
80 members drink either tea or coffee, but not both.
A + C = 80.
In the group, 10 drink neither.
D = 10.
A + B + C + D = 100.
So, B = (A + B + C + D) – (A + C) – D = 100 – 80 – 10 = 10.
How many members drink both tea and coffee can be determined. Sufficient.
C is the correct answer choice.
GMAT Overlapping Sets Practice Question 8
Written Explanation
A = Percentage of people who speak only English
B = Percentage of people who speak both English and French
C = Percentage of people who speak only French
A + B + C = 100%
A needs to be determined.
Statement (1)
80% speak English.
A + B = 80.
A cannot be determined. Insufficient.
Statement (2)
60% speak French.
B + C = 60.
A + B + C = 100%
So, A = 100 – 60 = 40%.
A can be determined. Sufficient.
B is the correct answer choice.
GMAT Overlapping Sets Practice Question 9
Written Explanation
Statement (1):
c = 10; Does not help in finding a. Insufficient.
Statement (2):
x + b = 60; Does not help in finding a. Insufficient.
Combining both, we know c = 10, x + b = 60; hence, a = 20. Sufficient.
Hence, C is the correct answer choice.
Facing difficulty with the approach for Set Theory questions? Please Click here
Facing difficulty with the approach for data sufficiency questions? Please Click here
Need a comprehensive strategy, approach, and practice for Set Theory? Please Click here (you need to be enrolled for a course that includes the Quant section).
Need a comprehensive strategy, approach, and practice for data sufficiency questions? Please Click here (you need to be enrolled for a course that includes the Quant section).
GMAT Overlapping Sets Practice Question 10
Written Explanation
Statement (1):
We do not know about the number of students with black eyes. Insufficient.
Statement (2):
We do not know about the numbers of boys. Insufficient.
Combining both, we do not know which students have black eyes. Any number of boys can have black eyes. Insufficient.
Hence, E is the correct answer choice.
Facing difficulty with the approach for Set Theory questions? Please Click here
Facing difficulty with the approach for data sufficiency questions? Please Click here
Need a comprehensive strategy, approach, and practice for Set Theory? Please Click here (you need to be enrolled for a course that includes the Quant section).
Need a comprehensive strategy, approach, and practice for data sufficiency questions? Please Click here (you need to be enrolled for a course that includes the Quant section).
How and Where to Practice GMAT Overlapping Sets Questions
Real practice for Overlapping Sets problems begins when you work on them in a software environment that closely mirrors the official GMAT interface. You need a platform that displays the overlapping sets information and questions in a GMAT style layout, lets you handle the data and answer choices in a natural way, and offers all the on screen tools and functions that you will use on the actual exam. Without this kind of realistic practice, it is difficult to feel fully ready for test day. High quality Overlapping Sets questions are not available in very large numbers. Among the limited but truly reliable sources are the official practice materials released by GMAC and the Experts’ Global GMAT prep online course.
Within the Experts’ Global GMAT online preparation course, every Overlapping Sets problem appears on an exact GMAT like user interface with all the real exam tools and features. You work through more than 50 Overlapping Sets questions in quizzes and also take 15 full-length GMAT practice tests that include several Overlapping Sets problems in roughly the same spread and proportion in which they appear on the actual GMAT.
All the best for your preparation!
