Invest 30 seconds...
...for what may lead to a life altering association!
Help Line
- +91.8800.2828.00 (IND)
- 1030-1830 Hrs IST, Mon-Sat
- support@expertsglobal.com
...for what may lead to a life altering association!


Inequalities describe relationships in which one quantity is greater than, less than, greater-than-or-equal-to, or less-than-or-equal-to another, usually requiring us to figure out the ranges of possible values rather than a single fixed answer. They play an important role in many algebraic problems on GMAT and are tested in abundance on the exam. Therefore, full coverage of inequalities is an essential part of any comprehensive GMAT preparation course. This page offers you an organized subtopic wise playlist, along with a few worked examples, for efficient preparation of this concept.
Modulus based or absolute value inequalities appear frequently on the GMAT. The central idea is that every modulus expression naturally splits into two separate cases, one positive and one negative. If you overlook either branch, you quietly lose a part of the solution set. For instance, to solve |x – 2| > 3, you must work through both x – 2 > 3 and x – 2 < -3. Many test takers skip the second inequality, and that is where avoidable errors enter. In the same way, for expressions like |x + 5| < 10, the logic changes shape and the variable must lie between two boundary values, -10 to 10. The following short video breaks down the approach, demonstrates it in detail, and prepares you to apply it in GMAT drills, sectional tests, and full-length GMAT mock tests.

Polynomial inequalities can appear daunting at first because the expressions look large, but the underlying idea is logical and highly structured. The GMAT rarely tests very bulky polynomials, yet building clarity on such examples ensures that even the most demanding cases feel manageable. The heart of the method lies in factorization and in studying how the polynomial behaves around its critical points. In your GMAT prep, once you learn to mark these points, plot them on a number line, and see how the signs change across intervals, the question turns into a graceful exercise in reasoning rather than a heavy calculation. This approach is known as the wavy curve method and is remarkably effective for solving factorization based inequalities on the GMAT. The following short video unpacks this concept and demonstrates its typical GMAT question forms.


Understanding how positive and negative numbers behave under multiplication and powers is one of the most basic yet powerful ideas in mathematics. In the GMAT Quant section, this knowledge becomes crucial in inequality questions and number property problems. A single slip with a sign can flip the entire answer, which makes such questions feel delicate. The core rules may seem straightforward at first: positive times positive stays positive, negative times negative becomes positive, and so on. However, once powers and inequalities enter together, the scenarios grow more layered. For instance, raising a negative number to an odd power versus an even power leads to completely different outcomes, and recognizing this difference makes all the impact. This quick video lesson presents the concept and shows how the GMAT is likely to test it.

Many GMAT questions on inequalities and functions require a very fine sense of how numbers behave across different ranges. Patterns that feel obvious for large values can completely reverse when you test numbers between −1 and 1. For instance, we usually expect 1/x to become smaller as x increases, but the exact reverse occurs when x lies between 0 and 1. In the same way, squaring a small fraction makes it even smaller, while taking its square root makes it larger. Similar reversals appear with negative numbers, where the behavior shifts once again. These subtle changes form the backbone of several higher level inequality problems. Without a firm grasp of these ranges, many students walk into traps, especially on advanced questions. In this short clip, the concept is explained step by step, along with how it can appear on the GMAT.

Some of the most challenging GMAT questions are those that use phrases such as “may be true,” “can be true,” or “must be true.” These are less about routine equation solving and more about testing conditions logically, deciding whether a statement works in at least one scenario or whether it holds in every possible case. In may be true or can be true problems, your goal is not to prove a rule forever but simply to find a single example that satisfies the statement; if one case fits, that option is acceptable. In contrast, must be true or always true questions reverse the requirement: if you can uncover even one situation where the statement does not hold, you must discard that choice. This brief video breaks down the idea and illustrates how GMAT questions can be built around it.

In this section, you will work through a collection of GMAT-style Inequalities questions, each accompanied by a clear, fully worked explanation. Approach every problem patiently and make deliberate use of the techniques and ideas you have just studied on this page for solving inequalities on the GMAT. At this point, place greater emphasis on following the stepwise method accurately than on simply arriving at the right option. After completing a question, use the explanation control to view the correct answer and to study the reasoning in a careful, descriptive manner.
Show Explanation

Written Explanation
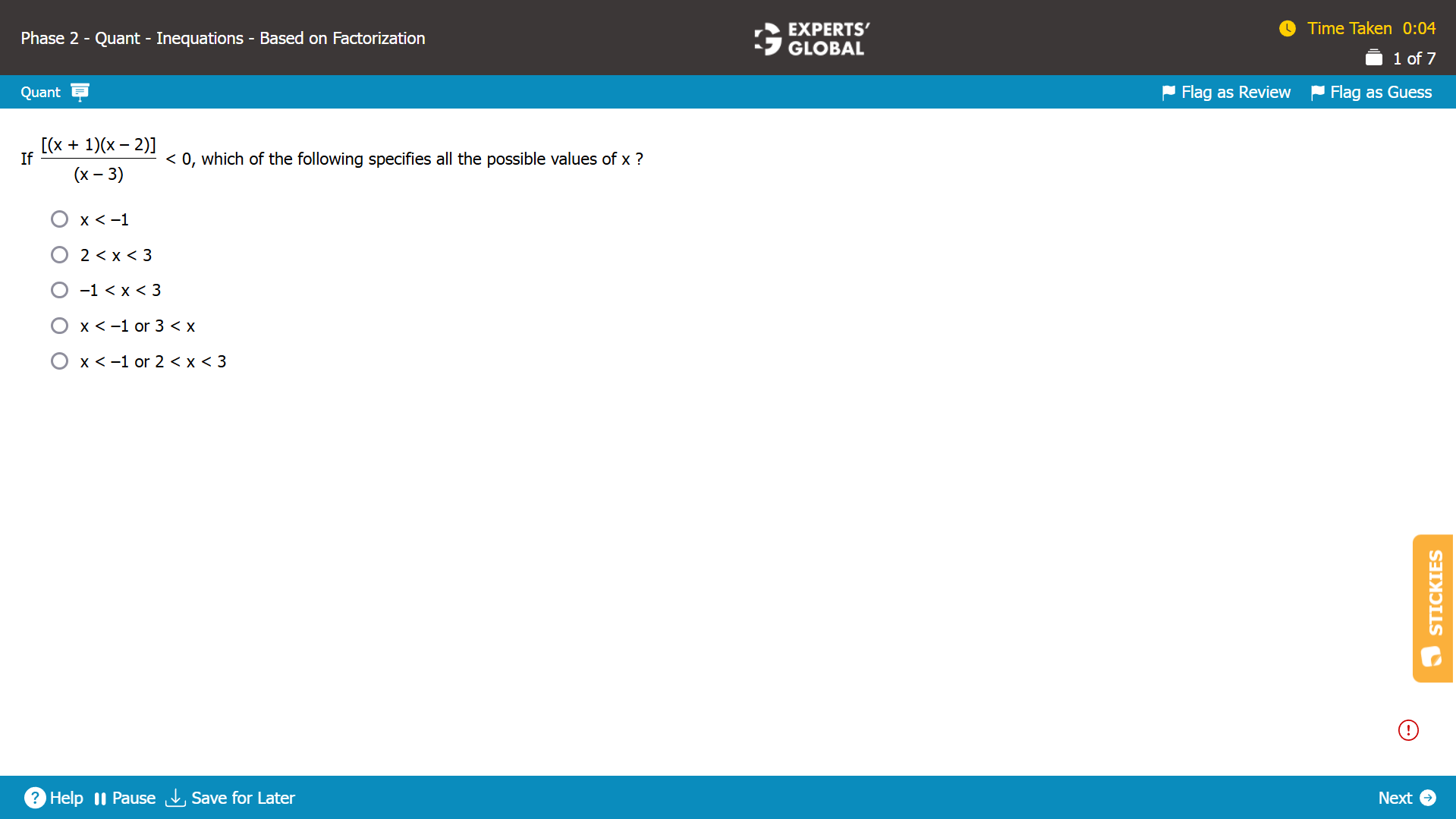
There are three terms in the function [(x + 1)(x – 2)] / (x – 3). So, there will be three nodes of the function.
At each of the five nodes, the value of the function would be zero, or undefined if there is division by zero.
The nodes will be (x + 1) = 0, (x – 2) = 0, and (x – 3) = 0.
The nodes are x = –1, x = 2, and x = 3.
On the number line, the nodes are –1, 2, and 3, in that order.
For a large value such as x = 10, the function is (10 + 1 ) (10 – 2) / (10 – 3) = 88/7 = Positive.
So, the value is positive for x > 3.
At the third node x = 3, the function has a zero in the denominator. So, the value is not defined at the third node x = 3.
Between x = 2 and x = 3, the function has negative values.
The value is zero at the second node x = 2.
Between x = –1 and x = 2, the function has positive values.
The value is zero at the first node x = –1.
The value is negative for x < –1.
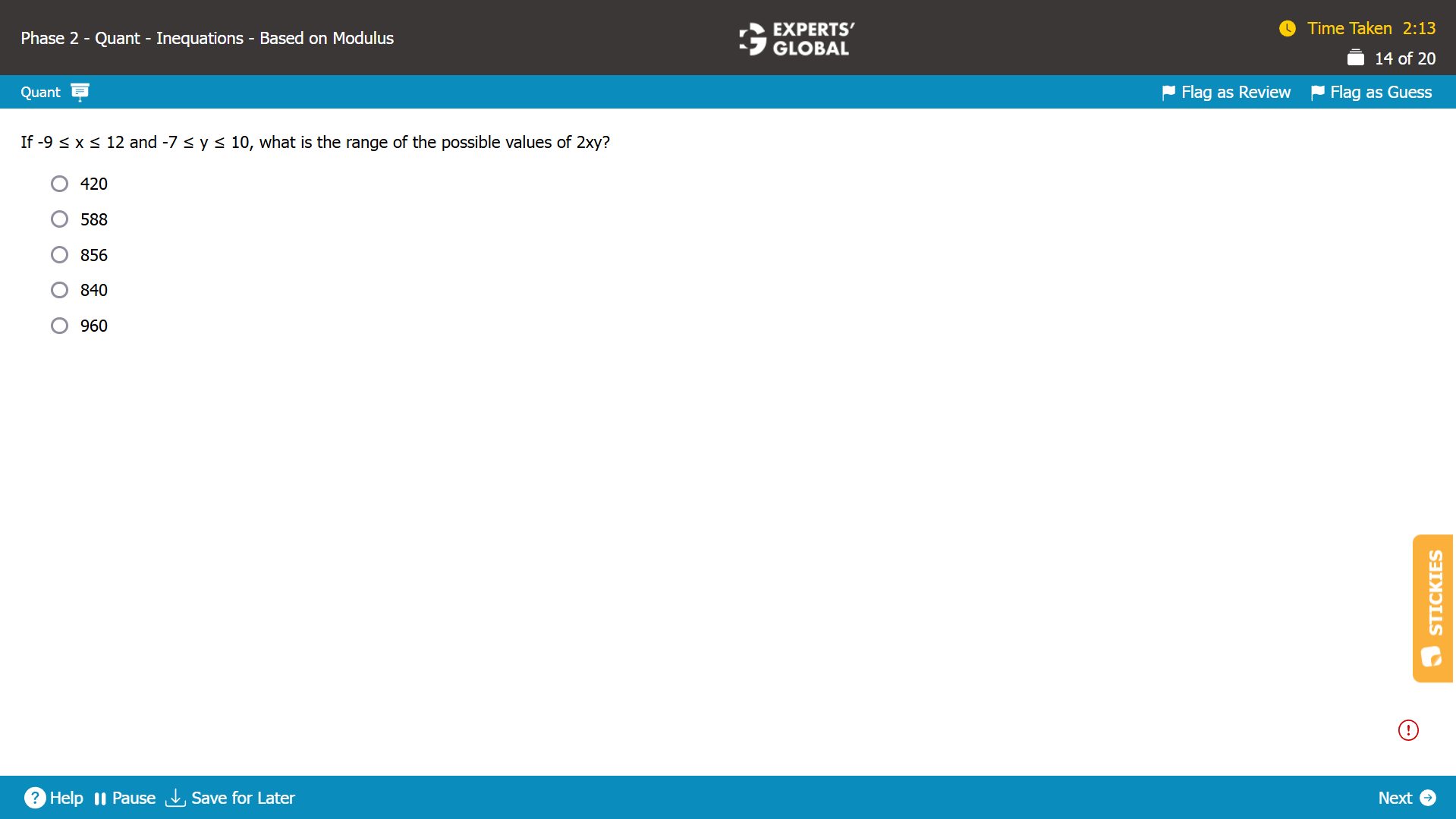
For [(x + 1)(x – 2)] / (x – 3) < 0, the values are possible when…
x < –1
or
between x = 2 and x = 3
The required range is x < –1 or 2 < x < 3.
E is the correct answer choice.
Show Explanation

Written Explanation
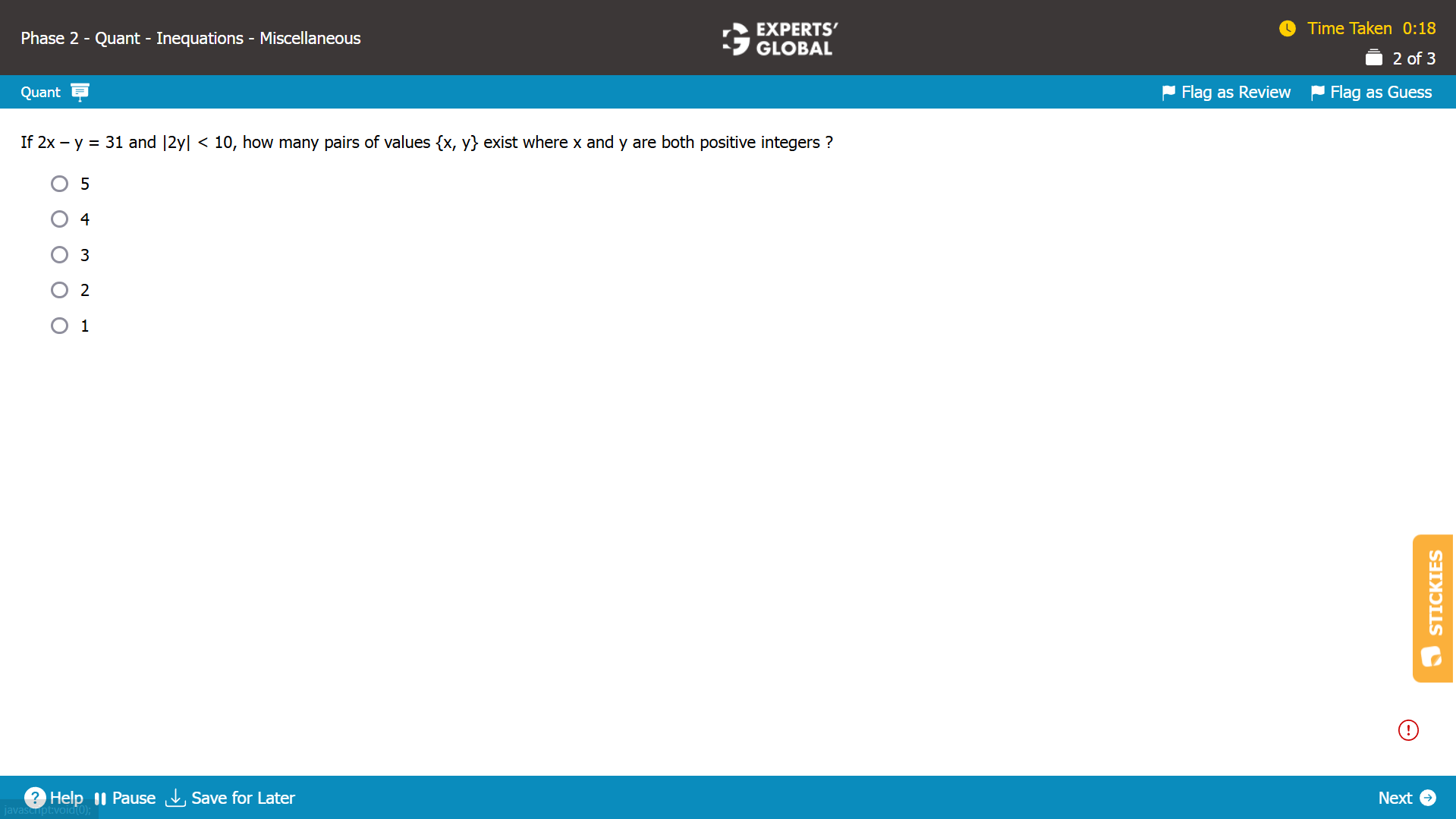
|2y| < 10
|y| < 5
Positive integer values of y can be {1, 2, 3, 4}
2x – y = 31
2x = 31 – y
x = (31 – y) / 2
When y = 1, x = (31 – (1)) / 2 = 30/ 2 = 15. x is a positive integer.
When y = 2, x = (31 – (2)) / 2 = 29/ 2. x is NOT a positive integer.
When y = 3, x = (31 – (3)) / 2 = 28/ 2 = 14. x is a positive integer.
When y = 4, x = (31 – (4)) / 2 = 27/ 2. x is NOT a positive integer.
The only positive integer values of x and y pair are…
x = 15 and y = 1
x = 14 and y = 3
2 pairs of values {x, y} exist such that x and y are both positive integers.
D is the correct answer choice.
Show Explanation

Written Explanation
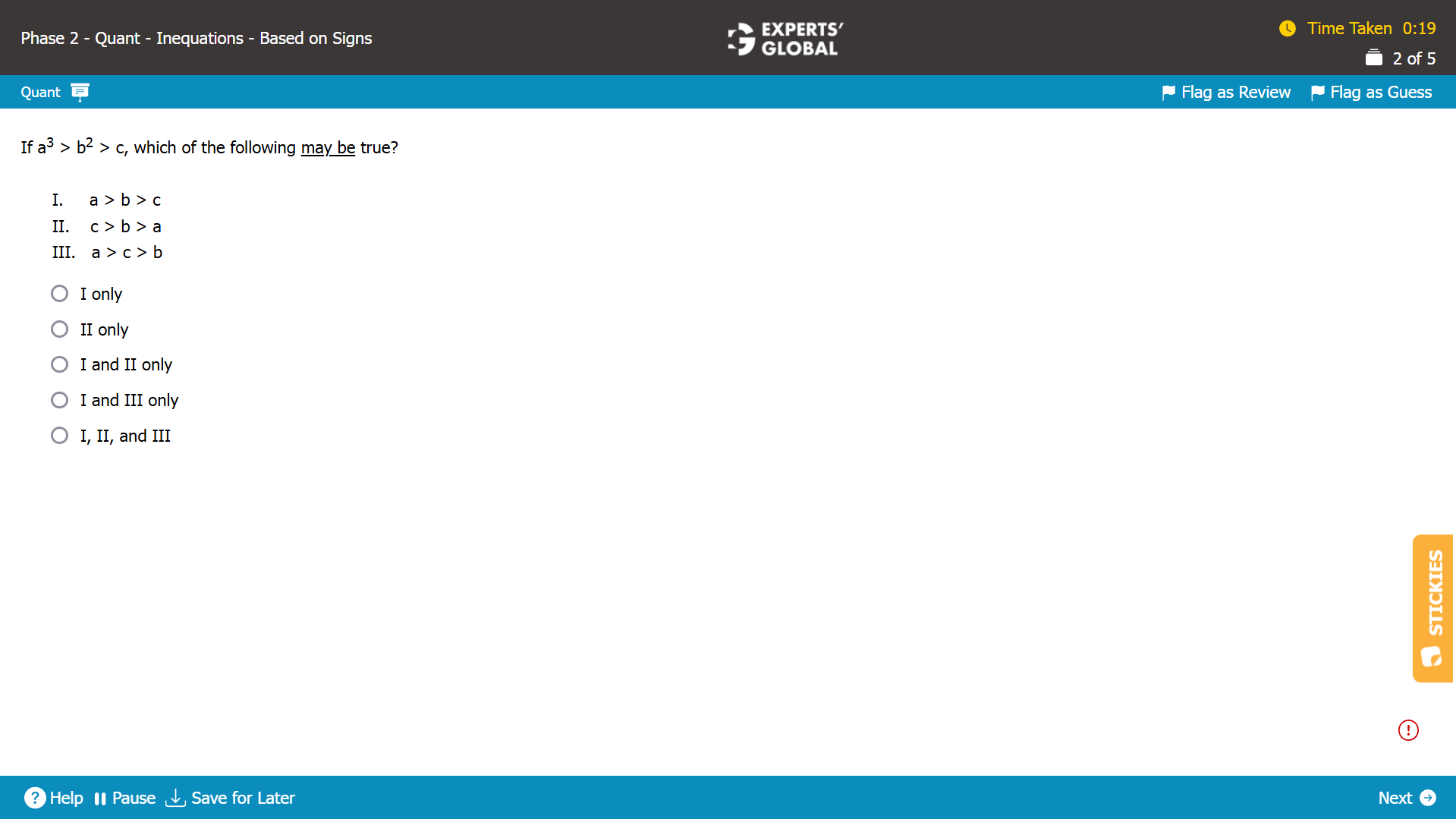
Let’s evaluate each statement.
Statement I: a > b > c.
Comparing a, b, and c, a > b > c and a3 > b2 > c.
This may be true for large positive values such as a = 5, b = 2, and c = 1.
a3 = 125, b2 = 4, and c = 1
a3 > b2 > c and a > b > c.
Statement I may be true for some values.
Statement II: c > b > a.
a3 > b2 > c and c > b > a.
This may be true for small positive values such as a = 1.9, b = 2, and c = 3.
a3 = 4.9, b2 = 4, and c = 1
a3 > b2 > c and c > b > a.
Statement II may be true for some values.
Statement III: a > c > b.
Comparing a and b, a > b and a3 > b2.
Comparing b and c, c > b and b2 > c.
This may be true for large positive values of a and small positive values of b and c, such as a = 5, b = 2, and c = 3.
a3 = 125, b2 = 4, and c = 1
a3 > b2 > c and a > c > b.
Statement III may be true for some values.
All of Statement I, Statement II, and Statement III may be true.
E is the correct answer choice.
Show Explanation

Written Explanation
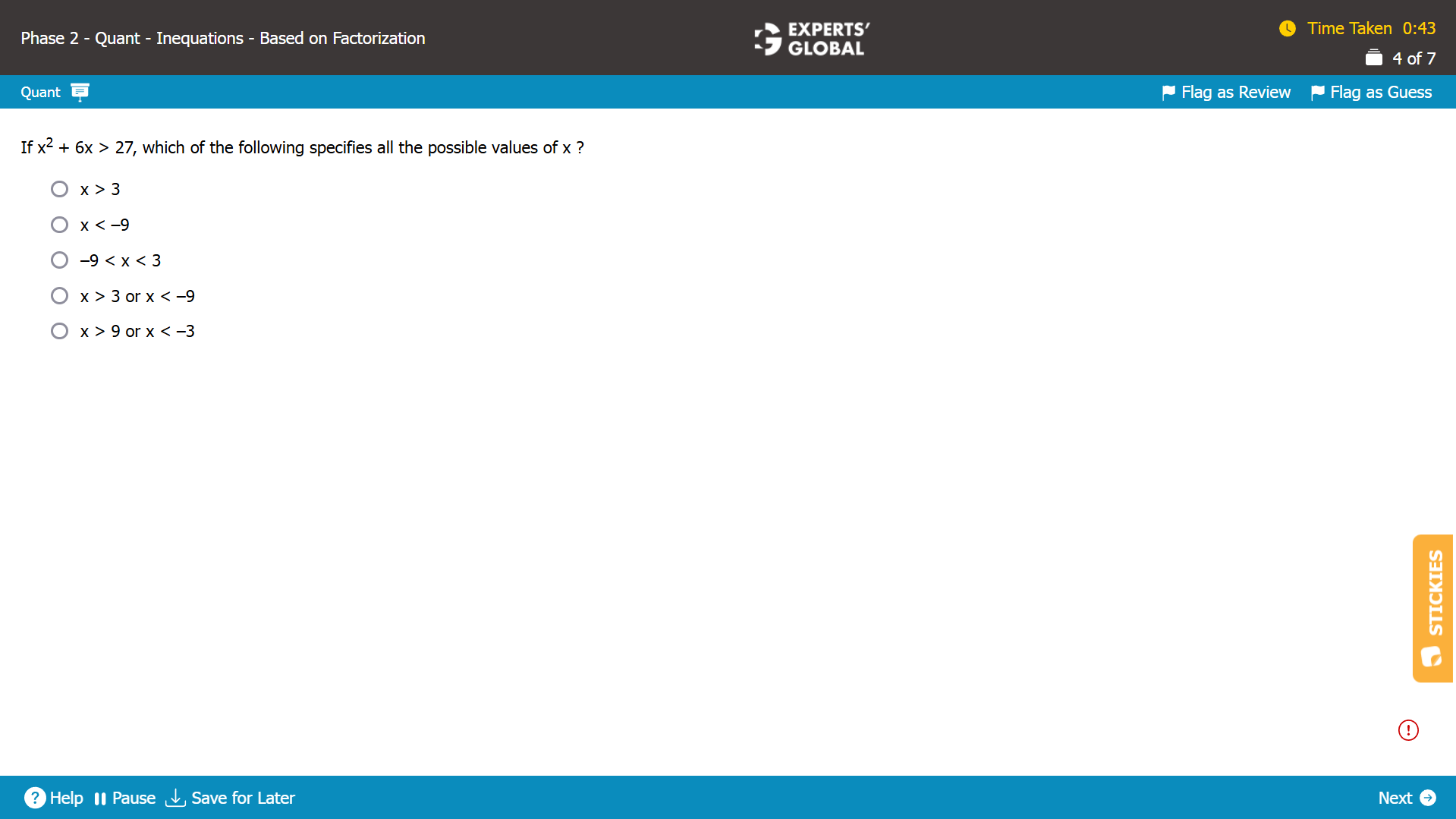
x2 + 6x > 27
x2 + 6x – 27 > 0
x2 + 9x – 3x – 27 > 0
x (x + 9) – 3 (x + 9) > 0
(x – 3) (x + 9) > 0
There are two terms in the function (x – 3) (x + 9). So, there will be two nodes of the function.
At each of the five nodes, the value of the function would be zero, or undefined if there is division by zero.
The nodes are x = 3 and x = –9.
On the number line, the nodes are –9 and 3, in that order.
For a large value such as x = 10, the function is (10 – 3) X (10 + 9) = 7 X 19 = Positive.
So, the value is positive for x > 3.
The value is zero at the second node x = 3.
Between x = –9 and x = 3, the function has negative values.
The value is zero at the first node x = –9.
The value is positive for x < –9.
For x2 + 6x > 27, or for (x – 3) (x + 9) > 0, the values are possible when…
x > 3
or
x < –9
The required range is x > 3 or x < –9.
D is the correct answer choice.
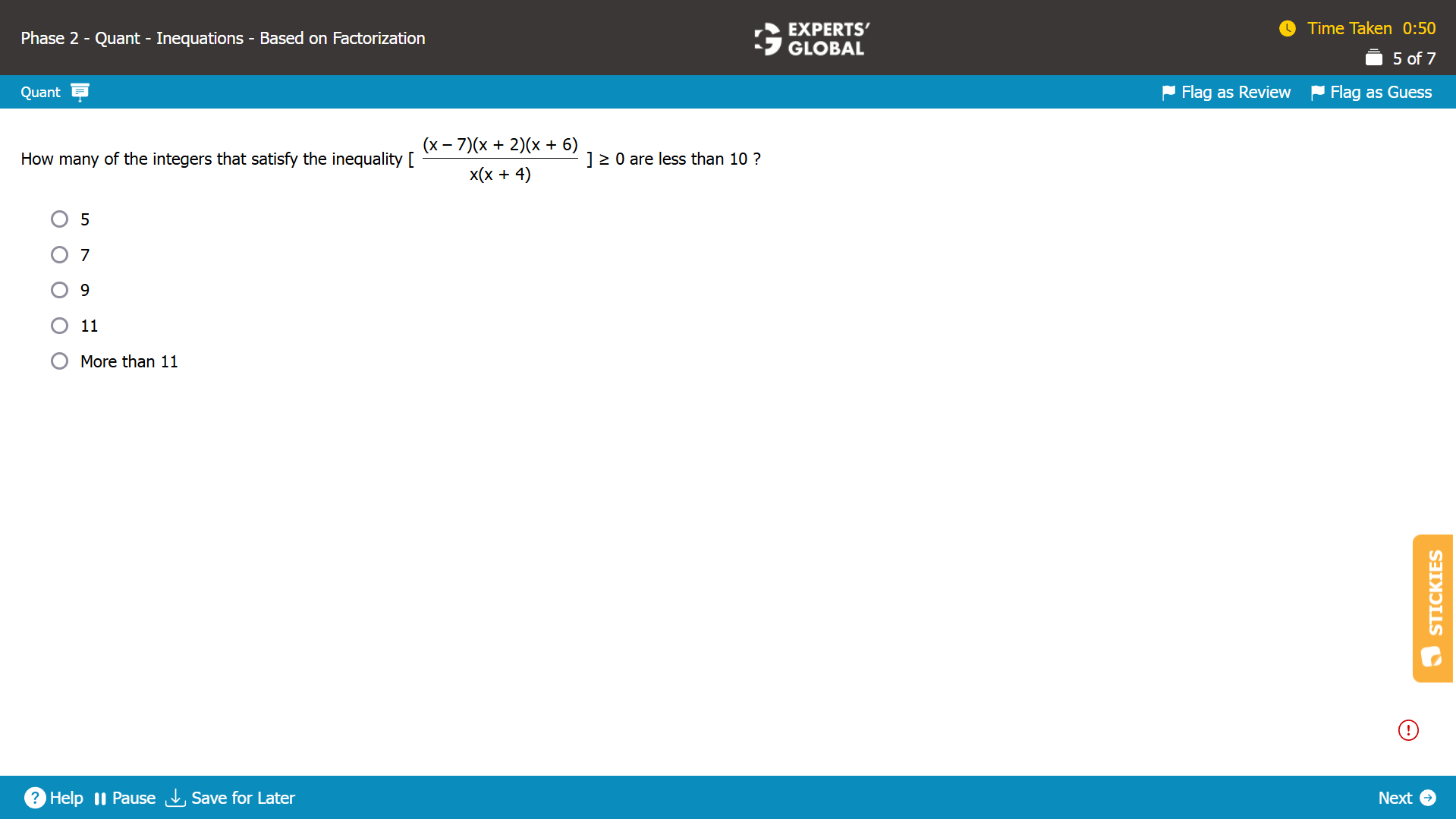
Show Explanation

Written Explanation
There are five terms in the function [ (x – 7)(x + 2)(x + 6) / x(x + 4) ]. So, there will be five nodes of the function.
At each of the five nodes, the value of the function would be zero or undefined.
The nodes will be (x – 7) = 0, (x + 2) = 0, (x + 6) = 0, x = 0, and (x + 4) = 0.
The nodes are x = 7, x = –2, x = –6, x = 0, and x = –4.
On the number line, the nodes are –6, –4, –2, 0, 7, in that order.
For a large value such as x = 10, the function is (10 – 7) (10 + 2) (10 + 6) / (10 X (10 + 4)) = 3 X 12 X 16 / (10 X 14) = Positive.
So, the value is positive for x > 7.
The value is zero at the fifth node x = 7.
Between x = 0 and x = 7, the function has negative values.
At the fourth node x = 0, the function has a zero in the denominator. So, the value is not defined at the fourth node x = 0.
Between x = –2 and x = 0, the function has positive values.
The value is zero at the third node x = –2.
Between x = –4 and x = –2, the function has negative values.
At the second node x = –4, the function has a zero in the denominator. So, the value is not defined at the second node x = –4.
Between x = –6 and x = –4, the function has positive values.
The value is zero at the first node x = –6.
The value is negative for x < –6.
For [ (x – 7)(x + 2)(x + 6) / x(x + 4) ] ≥ 0, the values are possible when…
x > 7
or
x = 7
or
Between x = –2 and x = 0
or
x = –2
or
Between x = –6 and x = –4.
or
x = –6
When x > 7, possible integer values less than 10 are {8,9} = 2
When x = 7, possible integer values less than 10 are {7} = 1
Between x = –2 and x = 0, possible integer values less than 10 are {–1} = 1
When x = –2, possible integer values less than 10 are {–2} = 1
Between x = –6 and x = –4, possible integer values less than 10 are {–5} = 1
When x = –6, possible integer values less than 10 are {–6} = 1
Total number of possible integer values less than 10 are 2 + 1 + 1 + 1 + 1 +1 = 7.
7 integers that satisfy the inequality [ (x – 7)(x + 2)(x + 6) / x(x + 4) ] ≥ 0 are less than 10.
B is the correct answer choice.
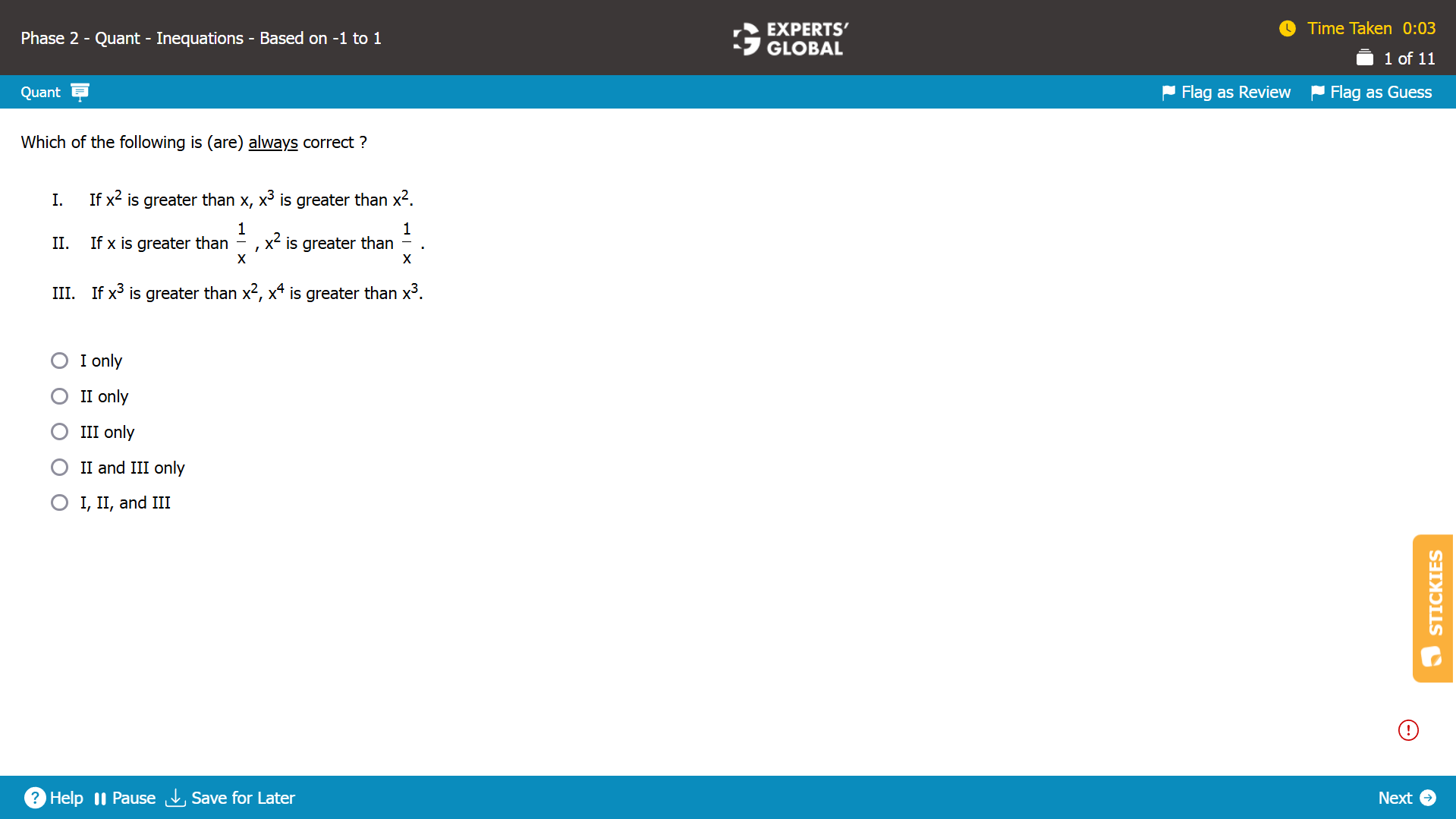
Show Explanation

Written Explanation
Let’s evaluate the first statement: If x2 is greater than x, x3 is greater than x2.
For x2 to be greater than x, x can be either positive and greater than 1 or negative.
Possibility 1: x is positive and greater than 1.
For example, x = 2, x2 = 4, and x3 = 8.
x2 is greater than x. x3 is greater than x2. Statement I holds.
Possibility 2: x is negative.
For example, x = –2, x2 = 4, and x3 = –8.
x2 is greater than x, but x3 is NOT greater than x2. Statement I does not hold.
Statement I is not always correct.
Let’s evaluate the second statement: If x is greater than 1 / x , x2 is greater than 1 / x .
For x to be greater than 1 / x, x has to be either positive and greater than 1, or x has to be negative and less than 1 in absolute value.
Possibility 1: x is positive and greater than 1.
For example, x = 2, 1 / x = 1 / 2, and x2 = 4.
x is greater than 1 / x. x2 is greater than 1 / x. Statement II holds.
Possibility 2: x is negative and less than 1 in absolute value.
For example, x = –1 / 2, 1 / x = –2, and x2 = 1 / 4.
x is greater than 1 / x. x2 is greater than 1 / x. Statement II holds.
Statement II is always correct.
Let’s evaluate the third statement: If x3 is greater than x2, x4 is greater than x3.
For x3 to be greater than x2, x has to be either positive and greater than 1, or x has to be negative and less than 1 in absolute value.
Possibility 1: x is positive and greater than 1.
For example, x = 2, x2 = 4, x3 = 8, x4 = 16.
x3 is greater than x2. x4 is greater than x3. Statement III holds.
Possibility 2: x is negative and less than 1 in absolute value.
For example, x = –1 / 2, x2 = 1 / 4, x3 = –1 / 8, x4 = 1 / 16.
x3 is greater than x2. x4 is greater than x3. Statement III holds.
Statement III is always correct.
Only Statement II and Statement III are always correct.
D is the correct answer choice.
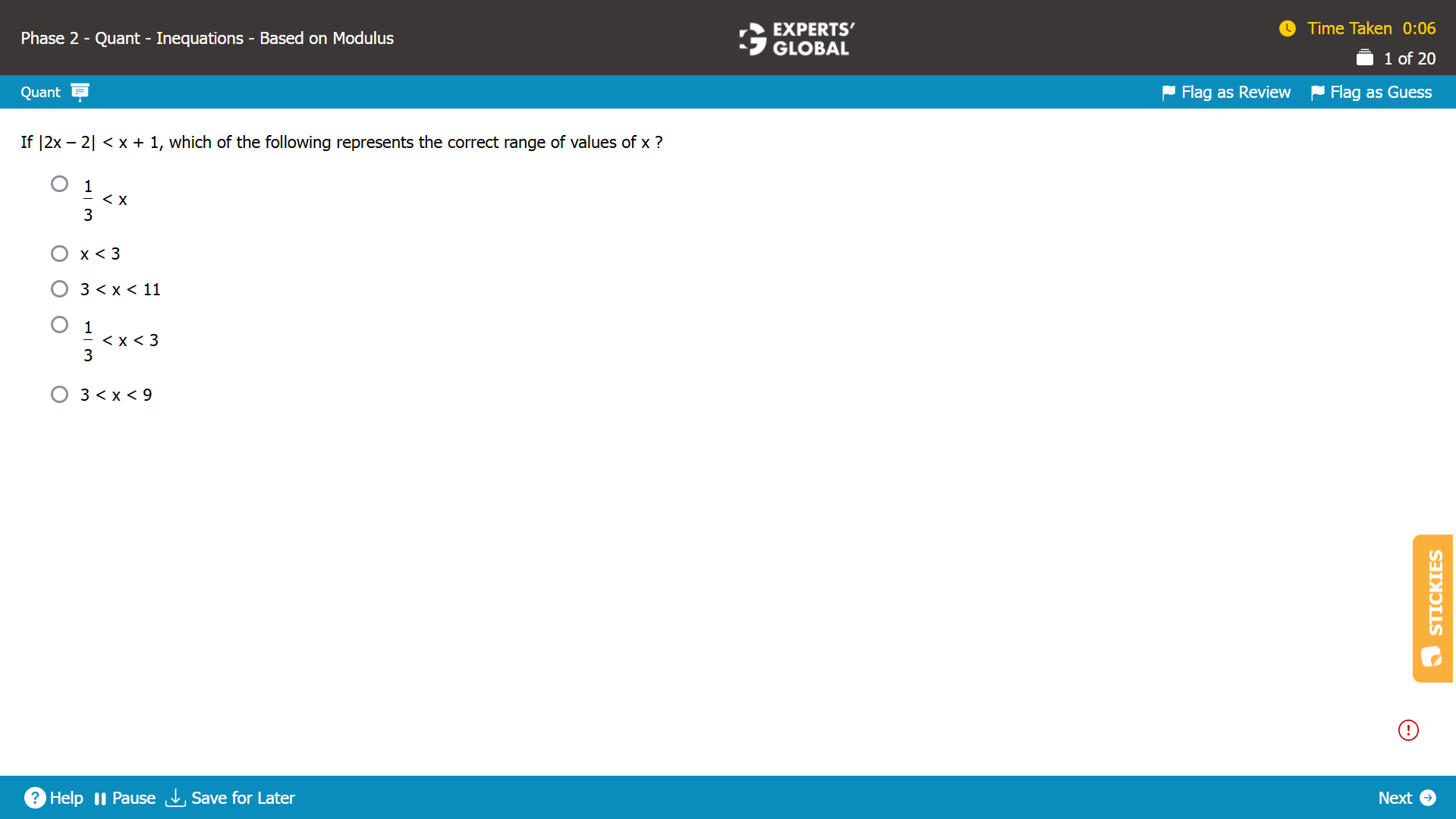
Show Explanation

Written Explanation
Removing the modulus sign leads to two possibilities.
So, for the inequality |2x – 2| < x + 1…
Possibility 1: (2x – 2) is positive.
(2x – 2) < x + 1
x < 3
x can be any number less than 3.
Possibility 2: (2x – 2) is negative.
(2x – 2) > (–1) X (x + 1)
(2x – 2) > –x – 1
3x > 1
x > 1 / 3
x can be any number greater than 1 / 3.
Combining all the possibilities, the range of x is 1 / 3 < x < 3.
D is the correct answer choice.
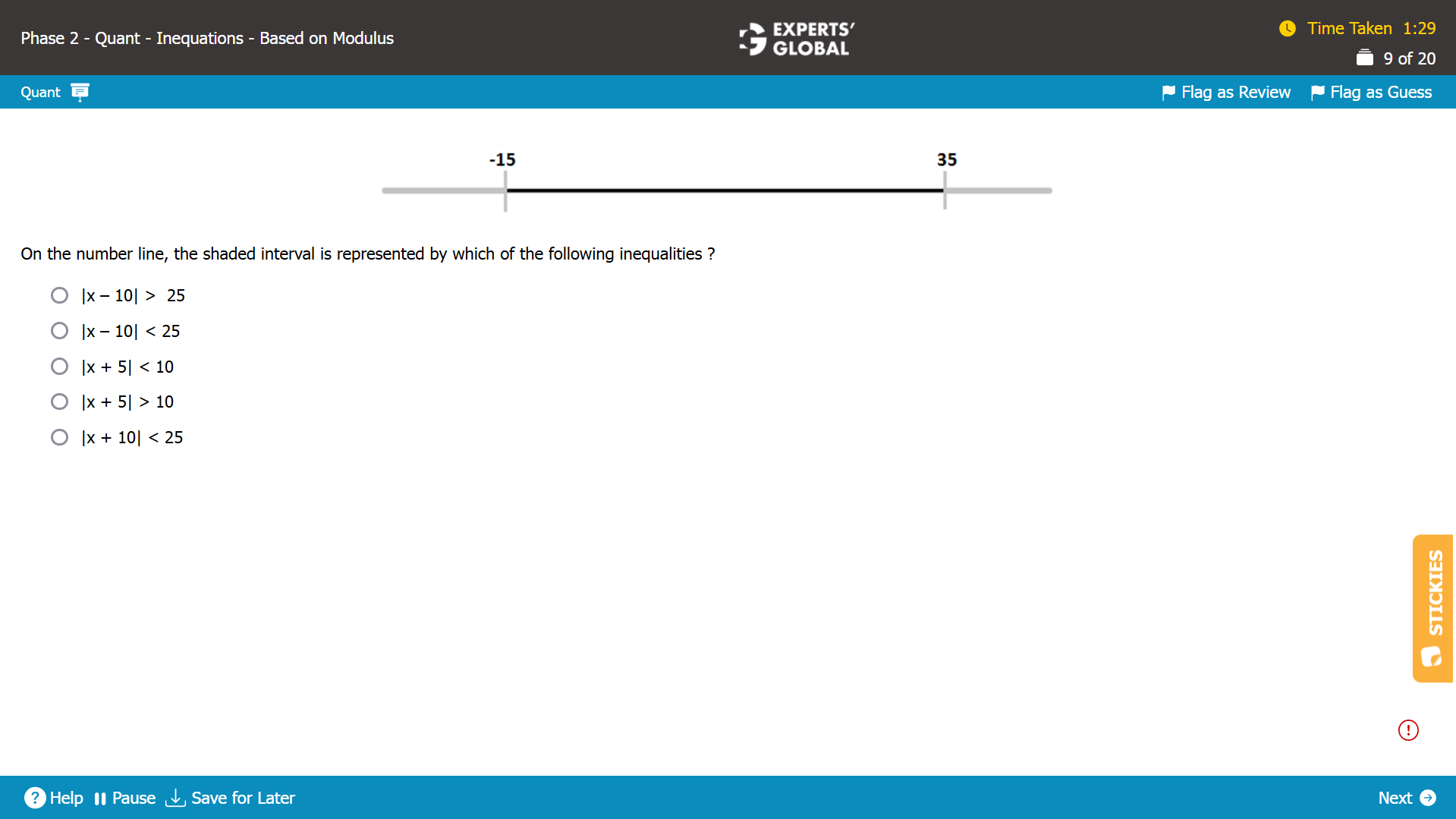
Show Explanation

Written Explanation
The shaded interval is –15 < x < 35.
Let’s evaluate each answer choice.
|x – 10| > 25.
So, (x – 10) > 25 or (x – 10) < –25
x > 35 or x < –15.
|x – 10| > 25 does not represent the range –15 < x < 35.
|x – 10| < 25.
So, (x – 10) < 25 or (x – 10) > –25
x < 35 or x > –15.
|x – 10| < 25 represents the range –15 < x < 35.
|x + 5| < 10.
So, (x + 5) < 10 or (x + 5) > –10
x < 5 or x > –15.
|x + 5| < 10 does not represent the range –15 < x < 35.
|x + 5| > 10.
So, (x + 5) > 10 or (x + 5) < –10
x > 5 or x < –15.
|x + 5| > 10 does not represent the range –15 < x < 35.
|x + 10| < 25.
So, (x + 10) < 25 or (x + 10) > –25
x < 15 or x > –35.
|x + 10| < 25 does not represent the range –15 < x < 35.
The shaded interval is represented by |x – 10| < 25.
B is the correct answer choice.
Show Explanation

Written Explanation
Statement (1)
2x + 5 > 2 – x
3x > –3
x > –1
x may or may not be greater than 1.
Whether x > 1 cannot be determined with certainty. Insufficient.
Statement (2)
|x – 12| = 12 – 3x.
Removing the modulus sign leads to two possibilities.
Possibility 1: (x – 12) is positive.
(x – 12) = 12 – 3x
4x = 24
x = 6
Possibility 2: (x – 12) is negative.
(x – 12) = –(1) X (12 – 3x)
x – 12 = –12 + 3x
0 = 2x
x = 0
The equation |x – 12| = 12 – 3x has x on both sides; so, the values of x need to be verified.
Verifying whether x = 6 is a valid value….
|x – 12| = |6 – 12| = |–6| = 6
12 – 3x = 12 – (3 X 6) = –6
The equation |x – 12| = 12 – 3x does not hold for x = 6. x cannot be equal to 6.
Verifying whether x = 0 is a valid value….
|x – 12| = |0 – 12| = |–12| = 12
12 – 3x = 12 – 0 = 12
The equation |x – 12| = 12 – 3x holds for x = 0. x can be equal to 0.
Overall, the only valid value of x is 0.
Whether x > 1 can be determined with certainty. Sufficient.
B is the correct answer choice.
Show Explanation

Written Explanation
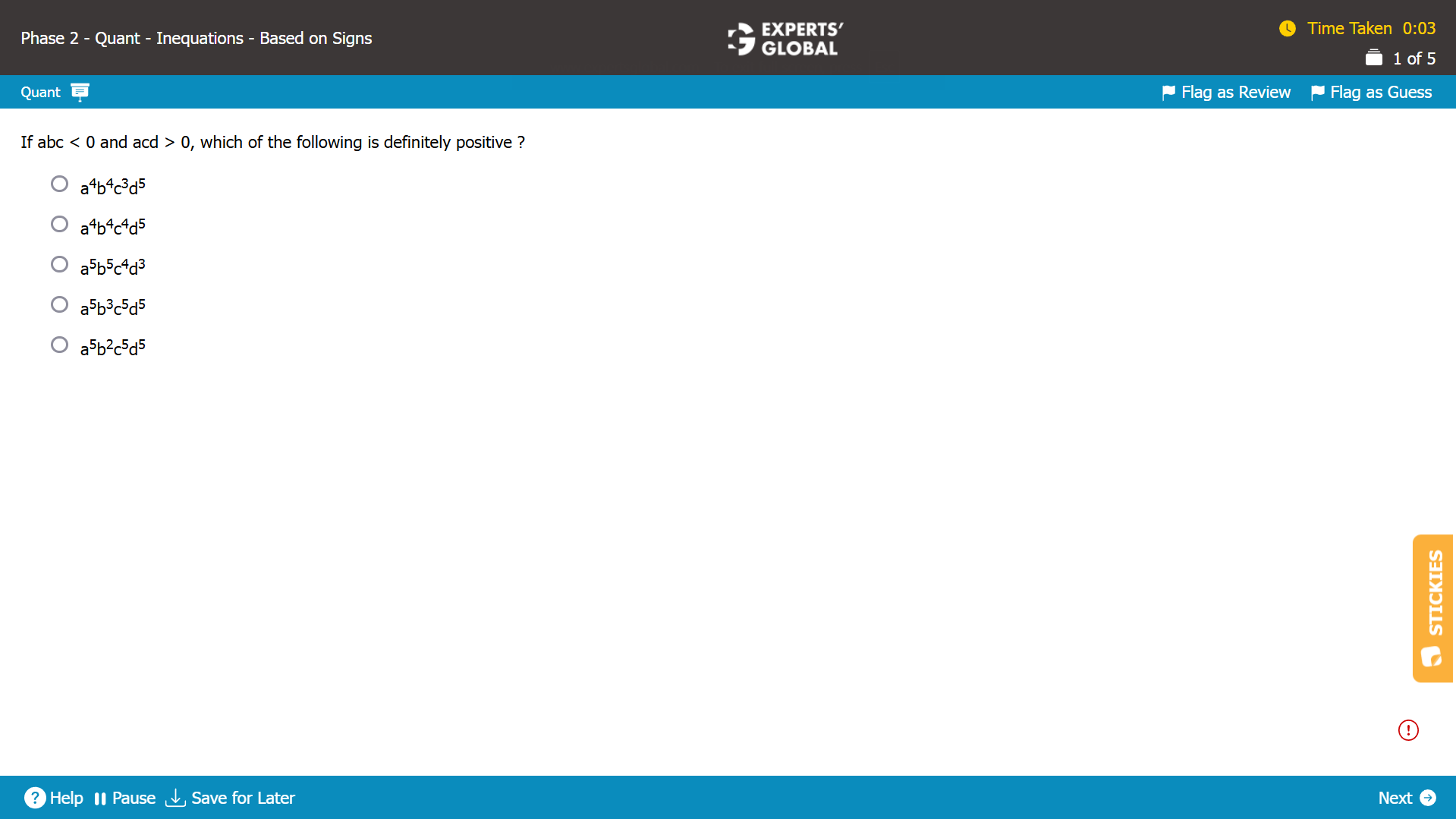
Even powers are always positive. So, let’s eliminate all even powers from each answer choice and evaluate further.
a4b4c3d5
Even powers are a4, b4, c2, and d4, all of which are positive.
So, the sign of a4b4c3d5 depends on the sign of cd.
Nothing can be said about the sign of cd from the given information that abc < 0 and acd > 0.
The sign of a4b4c3d5 cannot be determined with certainty.
a4b4c4d5
Even powers are a4, b4, c4, and d4, all of which are positive.
So, the sign of a4b4c4d5 depends on the sign of d.
Nothing can be said about the sign of d from the given information that abc < 0 and acd > 0.
The sign of a4b4c4d5 cannot be determined with certainty.
a5b5c4d3
Even powers are a4, b4, c4, and d2, all of which are positive.
So, the sign of a5b5c4d3 depends on the sign of abd.
Nothing can be said about the sign of abd from the given information that abc < 0 and acd > 0.
The sign of a5b5c4d3 cannot be determined with certainty.
a5b3c5d5
Even powers are a4, b2, c4, and d4, all of which are positive.
So, the sign of a5b3c5d5 depends on the sign of abcd.
Nothing can be said about the sign of abcd from the given information that abc < 0 and acd > 0.
The sign of a5b3c5d5 cannot be determined with certainty.
a5b2c5d5
Even powers are a4, b2, c4, and d4, all of which are positive.
So, the sign of a5b2c5d5 depends on the sign of acd.
acd > 0.
So, a5b2c5d5 is definitely positive.
[Alternatively,
acd > 0
Any power of acd will be greater than 0.
So, let’s try to reduce each expression by a certain power of acd.
a4b4c3d5 = (acd)3 X ab4d2
So, the sign of a4b4c3d5 depends on the sign of ab4d2.
.
Nothing can be said about the sign of ab4d2 from the given information that abc < 0 and acd > 0.
The sign of a4b4c3d5 cannot be determined with certainty.
a4b4c4d5= (acd)4 X b4d
So, the sign of a4b4c4d5 depends on the sign of b4d.
Nothing can be said about the sign of b4d from the given information that abc < 0 and acd > 0.
The sign of a4b4c4d5 cannot be determined with certainty.
a5b3c5d5 = (acd)5 X b3
So, the sign of a5b3c5d5 depends on the sign of b3.
Nothing can be said about the sign of b3 from the given information that abc < 0 and acd > 0.
The sign of a5b3c5d5 cannot be determined with certainty.
a5b2c5d5 = (acd)5 X b2
So, the sign of a5b2c5d5 depends on the sign of b2.
Even powers are always positive. b2 is positive.
So, a5b2c5d5 is definitely positive.]
E is the correct answer choice.
Real practice for Inequalities problems begins when you work on them through a software simulation that closely mirrors the official GMAT interface. You need a platform that presents the question stem and the inequality information in a GMAT like layout, lets you interact with the conditions and answer choices naturally, and provides all the on screen tools and functionalities that you will see on the actual exam. Without this kind of environment, it is difficult to feel fully prepared for test day. High quality Inequalities questions are not available in large numbers. Among the limited, genuinely strong sources are the official practice materials released by GMAC and the Experts’ Global GMAT course.
Within the Experts’ Global GMAT online preparation course, every Inequalities problem appears on an exact GMAT like user interface that includes all the real exam tools and features. You work through more than 100 Inequalities questions in quizzes and also take 15 full-length GMAT mock tests that include several Inequalities questions in roughly the same spread and proportion in which they appear on the actual GMAT.
All the best!