Invest 30 seconds...
...for what may lead to a life altering association!
Help Line
- +91.8800.2828.00 (IND)
- 1030-1830 Hrs IST, Mon-Sat
- support@expertsglobal.com
...for what may lead to a life altering association!


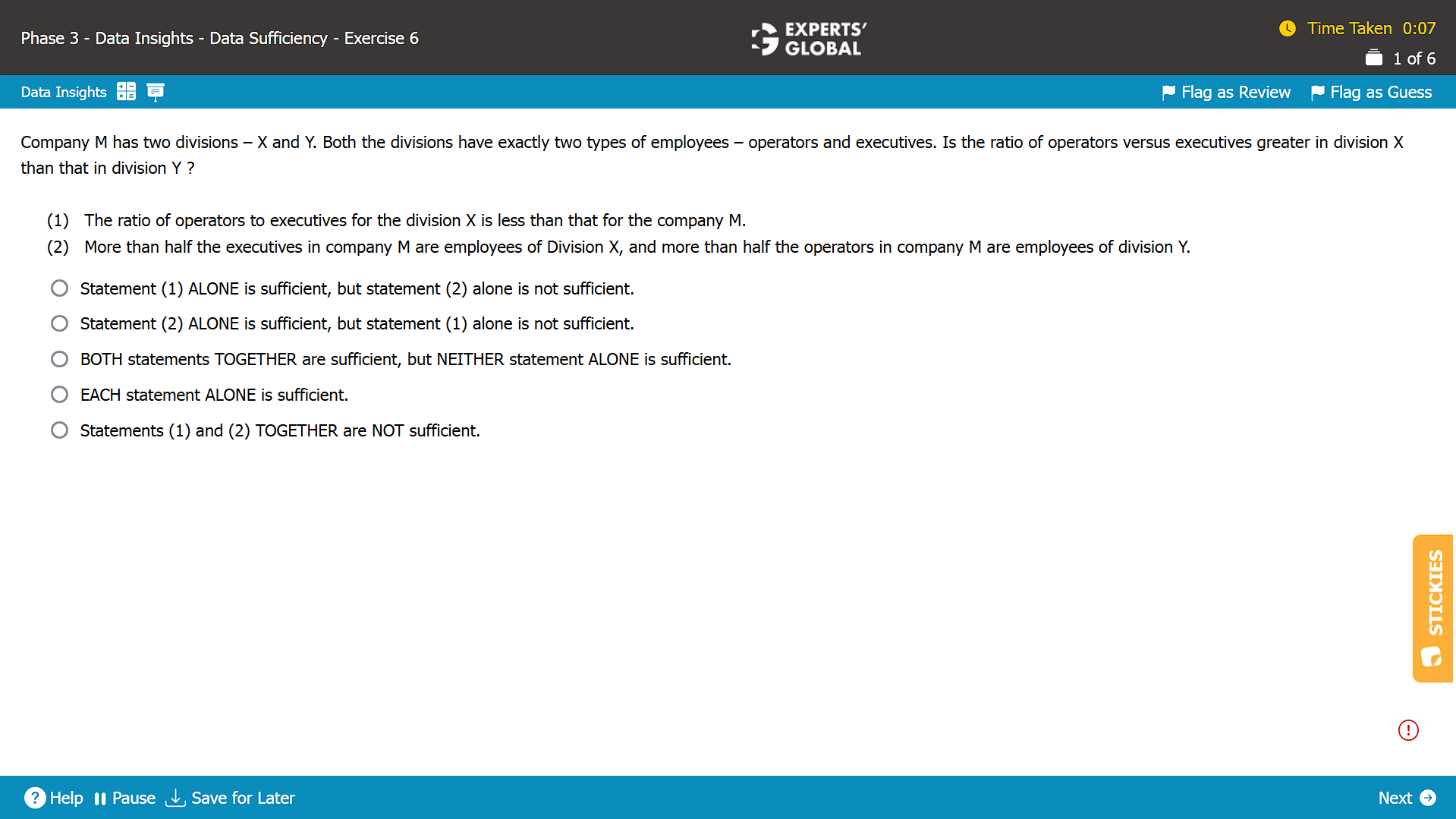
Data Sufficiency questions in the GMAT Data Insights section test your ability to assess whether the information provided is sufficient to answer a question. Each set includes a question and two statements. You must evaluate if the statements, separately or together, provide enough data to solve the problem. This format tests logic, structure, and disciplined reasoning.
To familiarize with all GMAT question types, take the first of our 15 full-length GMAT practice tests free
Data Sufficiency questions in the GMAT’s Data Insights section are designed to reflect how professionals evaluate incomplete or partial data before making decisions. These questions test whether you can determine the sufficiency of information rather than compute exact solutions. A typical Data Sufficiency item consists of a problem statement followed by two numbered statements. Your task is to assess whether the provided statements, alone or in combination, give enough information to answer the question. This structure mirrors real-world situations in which managers must decide whether they have enough facts to act. A high-quality GMAT prep course can help you build the analytical discipline required to succeed in this format.
Each Data Sufficiency question includes a question stem, followed by two statements labeled (1) and (2). Your job is not to solve the problem, but to decide whether you could solve it using the given information. The five answer choices always remain the same:
A. Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
B. Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
C. BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
D. EACH statement ALONE is sufficient
E. Statements (1) and (2) TOGETHER are NOT sufficient
This unique format does not reward brute-force calculation. Instead, it evaluates logical precision, pattern recognition, and reasoning clarity.

Correct Answer: D
This question type tests your ability to evaluate the usefulness and completeness of information. The key skills tested include:
You must determine whether a given piece of data, alone or combined with another, is enough to answer a question. This skill is central to business analytics and decision-making.
Data Sufficiency questions often involve basic arithmetic, algebra, number properties, or ratios. The focus is on understanding relationships, spotting constraints, and determining uniqueness, not lengthy calculations.
While some DS questions are numeric, many test your ability to reason through conditions, compare logical scenarios, and interpret relationships. This includes evaluating definitions, parsing statements, and interpreting word problems that involve conditional logic or categorical reasoning.
Over time, you begin to identify recurring logical structures and common traps. This makes your evaluation faster and more precise.
Words such as “must,” “could,” or “only” carry significant weight. Even small modifiers can shift the sufficiency status of a statement.

Seek quick GMAT prep? Explore our GMAT crash course
Is the value of x equal to 3?
Statement (1): x² = 9
Statement (2): x > 0
A. Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
B. Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
C. BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
D. EACH statement ALONE is sufficient
E. Statements (1) and (2) TOGETHER are NOT sufficient
We need to determine whether x = 3.
We must assess each statement independently to determine whether one or both are sufficient. If neither statement is sufficient alone, we then evaluate whether they are sufficient when considered together.
x² = 9
Taking the square root on both sides, we get;
x = –3 or x = 3
Since x can either be –3 or 3, it is NOT possible to determine with certainty the value of x. Hence, Statement (1) is insufficient.
x > 0
Since x can be any positive number, x may or may not be 3. Hence, Statement (2) is insufficient.
As Statement (1) alone as well as Statement (2) alone is insufficient to answer the question, we need to now combine the two statements.
Only x = 3 satisfies both statements.
It is possible to determine with certainty that x = 3. Hence, Statement (1) and Statement (2) combined are sufficient.
C is the correct answer choice.
Correct Answer: D
Roughly 50 percent of Data Sufficiency questions on the GMAT are word problems . These questions are framed in sentences rather than equations and often involve conditions, relationships, or quantities described in words. To do well, you must read carefully, understand what is being asked, and judge whether the given information is enough to answer it. With practice, word problems can become a key strength.
To master Data Sufficiency questions, you must combine conceptual understanding with disciplined reasoning. Here are some key tips:
The five choices never change. Knowing them by heart allows you to work methodically.
Always examine each statement alone. Only consider them together if neither is sufficient independently.
Focus on whether the information is enough. Do not waste time calculating the final value unless it helps establish sufficiency.
When the problem involves variables, test multiple values to check for uniqueness or contradiction. This is especially useful for number properties and inequalities.
Use the process of elimination as you progress through the question. This saves time and reduces error.
Some statements may repeat or imply the same condition. Identifying these can help you avoid overestimating the value of combined data.
High-performing students often lose points in DS due to preventable errors. Here are the most frequent traps:
Never combine statements unless both are clearly insufficient on their own.
If a statement or a combination of statements allows for more than one possible answer, it is not sufficient. A sufficient condition must lead to one and only one valid solution.
You are not required to calculate the exact answer. Data Sufficiency is about evaluating whether the information provided is enough to solve the problem, not about finding the final value. Focus on determining sufficiency, and avoid unnecessary math that does not contribute to that goal.
A statement is sufficient if it leads to a definite Yes or No. For example, if the question asks whether x = 5, and a statement says x is negative, the answer is clearly “No”. Since the answer is definite, the statement is sufficient.
Rely only on the information given. Do not assume unstated values, conditions, or relationships.
Watch out for subtle wording changes. “Is x = 3?” is different from “What is the value of x?”
Some conditions may appear sufficient until you consider an exception. Always test edge cases, such as zero, negative numbers, or extremes, to confirm that your conclusion holds.
To develop a consistent and confident approach to Data Sufficiency, we recommend a three-phase framework. At Experts’ Global, we call this Understand, Practice, and Master. This structure allows you to build from foundational awareness to expert-level performance.
Start by building clarity on what Data Sufficiency questions are truly testing. Learn to identify sufficiency logic, evaluate constraint-based scenarios, and avoid the urge to solve. Familiarize yourself with topics such as number properties, ratios, algebra, and logical deduction. Understand how the GMAT designs traps involving overlapping information or ambiguous phrasing. A well-designed GMAT prep course that trains your conceptual thinking, rather than formula memorization, is ideal at this stage.
Engage in regular practice with questions from official and reliable third-party resources. Solve a broad mix to develop pattern recognition. After each session, reflect on whether your error was due to misunderstanding, misreading, or faulty logic. Build an error log to monitor recurring mistakes. Focus not only on answering correctly but on being efficient and confident. This is the stage where your logic begins to crystallize, and your accuracy improves with speed.
In the final phase, include Data Sufficiency questions in full-length GMAT mock exams and timed sections. Simulate real test-day conditions to build stamina. Track performance by type and topic. Focus especially on your pacing, your ability to avoid assumptions, and your confidence in evaluating information without overthinking. Reinforce strategies that reduce hesitation. Review your toughest questions repeatedly. This stage transforms effort into execution, making you prepared for even the trickiest DS items on test day.
Data Sufficiency questions draw from a broad set of topics covered in the GMAT Data Insights syllabus. While they may seem mathematical, their conceptual range is wide. Some common formats include:
A result-oriented MBA admission consultants can support you not just with your applications but also with your GMAT preparation if you begin early enough. They can guide you on effective preparation strategies, keep you motivated and accountable, and help you avoid common mistakes. Most importantly, they can assist with profile enhancement alongside your prep, ensuring that your entire application journey is cohesive, focused, and aligned with your long-term goals.
Data Sufficiency questions on the GMAT are designed not to test complex math, but to assess how you think. They reflect a higher-order skill that business schools and employers value deeply: the ability to make sound decisions when data is partial or incomplete. By learning to evaluate sufficiency with precision, you sharpen your reasoning and reduce wasted effort. The right approach, built patiently and practiced consistently, can turn this intimidating format into one of your biggest strengths on the GMAT.
Advance your journey with our GMAT prep course and MBA consulting bundle