Invest 30 seconds...
...for what may lead to a life altering association!
Help Line
- +91.8800.2828.00 (IND)
- 1030-1830 Hrs IST, Mon-Sat
- support@expertsglobal.com
...for what may lead to a life altering association!


Ratios compare two quantities. Proportion is the relationship between two equal ratios or between a part and the whole. Variation describes how one quantity changes when another changes. A proper understanding of these concepts is an essential part of any comprehensive GMAT preparation course. This page provides an organized subtopic wise playlist, along with a few worked examples, for steady preparation of this concept



Proportion questions often unsettle students because they look simple on the surface, yet a small hidden idea changes everything. The crucial insight is that a ratio such as A:B = 1:3 does not claim that A is 1 and B is 3. It tells you that A and B stand in this relationship through common multiples, whether those values are large or small, positive or negative. Seeing this clearly is the starting point for handling proportion based questions with speed and accuracy. A popular GMAT pattern adjusts A and B by certain amounts and then sets them equal to a new ratio. Once you express each term in relation to a single constant, such questions unfold in a clean, straightforward manner. The short video below presents this approach, shows how it functions on real questions, and prepares you to use it in GMAT drills, sectional tests, and full-length GMAT simulations.

Variation questions on the GMAT grow naturally out of ratio and proportion problems, but they call for a deeper sense of how quantities relate to one another. Instead of working only with simple ratios, you now meet the ideas of constants and proportionality. A quantity may change directly with one variable, inversely with another, or through a blend of both. The central task is to turn these worded relationships into clear mathematical statements and then solve them calmly, step by step. For example, if A varies directly as the square of B and inversely as C, you express this as A ∝ (B² / C). When you replace the proportionality sign, a constant enters the equation, and you can plug in values to find unknowns. With patient, thoughtful practice, these questions begin to feel straightforward and manageable. The brief video that follows explains this idea step by step and shows how it can be tested on the GMAT.

In this section, you will find a series of GMAT-style Ratio, Proportion, and Variation questions, each paired with a careful, stepwise explanation. Work through every problem at a steady pace and consciously use the methods and ideas you have just studied on this page for solving Ratio, Proportion, and Variation questions on the GMAT. At this point, give more importance to applying the structured approach correctly than to simply obtaining the right answer. After attempting each question, use the explanation toggle to view the correct response and read the full descriptive reasoning.
Show Explanation

Written Explanation
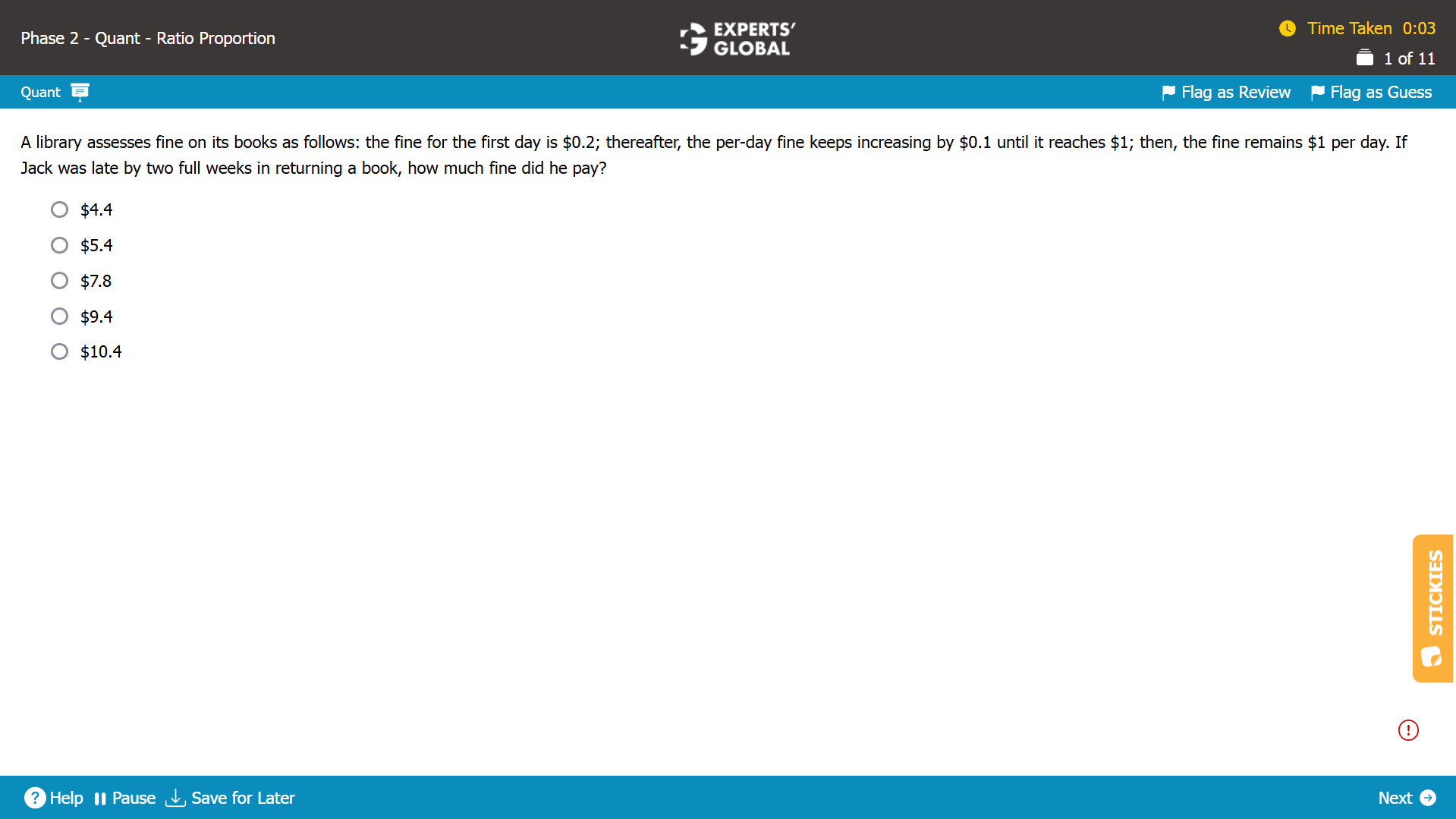
For two weeks i.e. 14 days, the fine would be as follows
0.2 + 0.3 + 0.4 + 0.5 + 0.6 + 0.7 + 0.8 + 0.9 + 1.0 + 1 + 1 + 1 + 1 + 1 = $10.4
Hence, E is the correct answer choice.
Show Explanation

Written Explanation
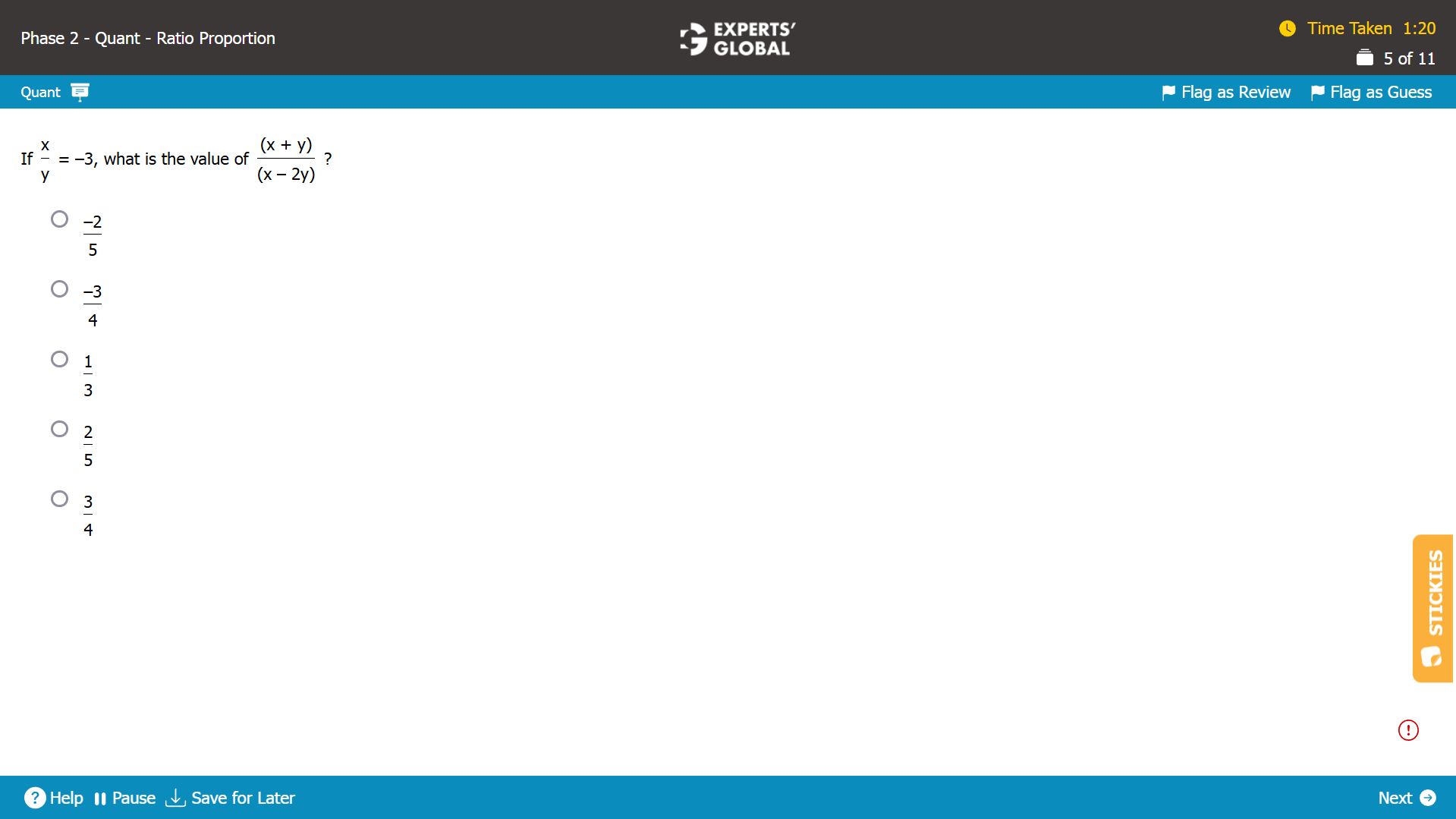
x / y = –3
x = –3y
So,
(x + y) = (–3y) + y = –2y
(x – 2y) = (–3y) – 2y = –5y
So,
(x + y) / (x – 2y) = –2y / –5y = 2/5.
D is the correct answer choice.
Show Explanation

Written Explanation
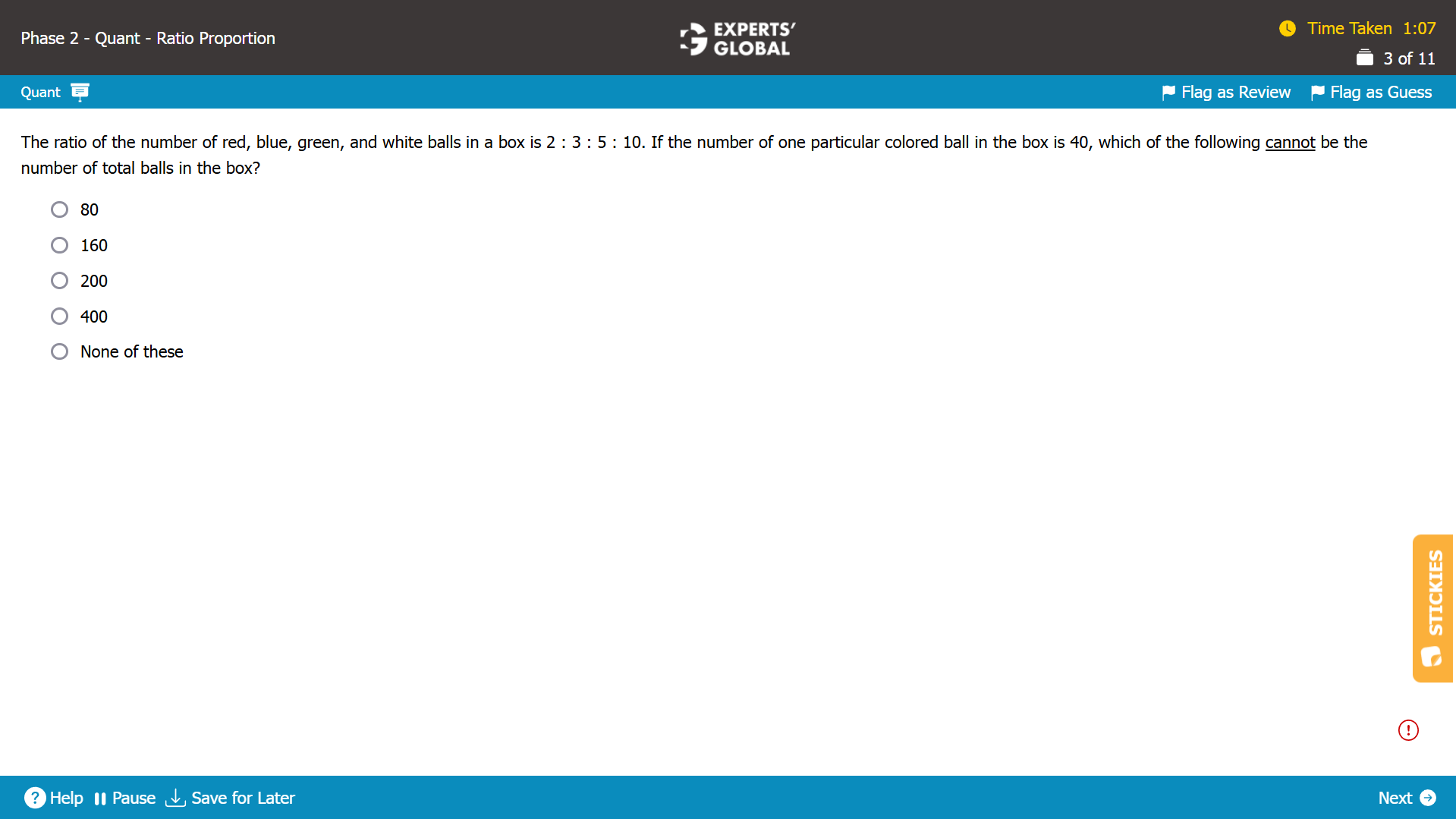
Let’s say that there are 2x red balls, 3x blue balls, 5x green balls, and 10x white balls.
Total number of balls = 2x + 3x + 5x + 10x = 20x.
If there are 40 red balls, 2x = 40; x = 20.
So, total number of balls = 20x = 400 balls.
If there are 40 blue balls, 3x = 40; x = 13.33. Because the number of balls is an integer, this possibility cannot exist.
If there are 40 green balls, 5x = 40; x = 8.
So, total number of balls = 20x = 160 balls.
If there are 40 white balls, 10x = 40; x = 4.
So, total number of balls = 20x = 80 balls.
Overall, it is possible to have 400, 160, and 80 total balls. So, answer choice A, answer choice B, and answer choice D can be ruled out. Answer choice C, with 200 balls, is not a possibility.
C is the correct answer choice.
Show Explanation

Written Explanation
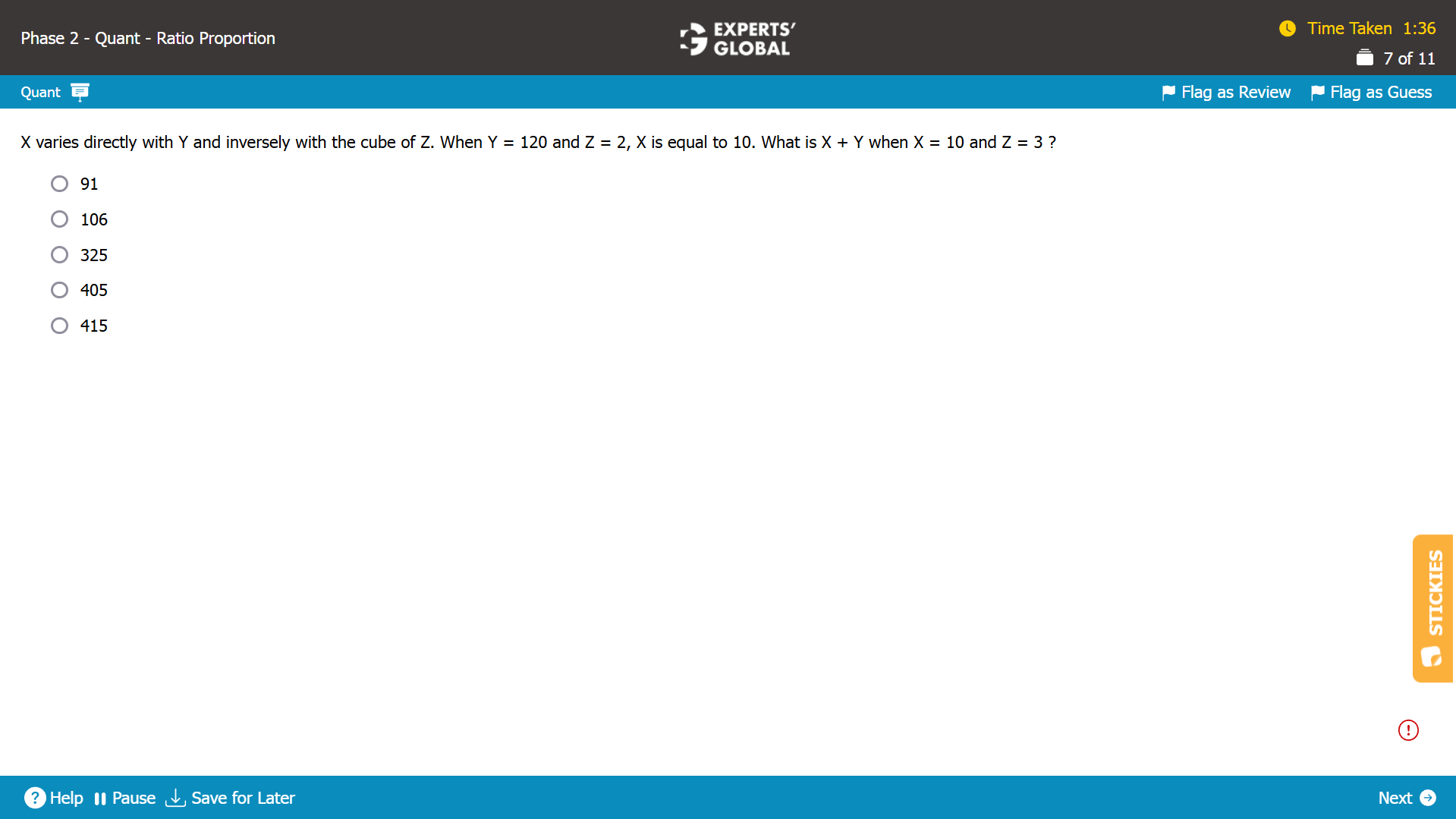
X = k X Y / Z3
10 = k X (120) / (23)
k = 10 X 8 / 120 = 2 / 3.
When X = 10 and Z = 3
10 = (2 / 3) X Y / (33)
Y = 10 X (3 / 2) X 27 = 405.
So, X + Y = 10 + 405 = 415.
E is the correct answer choice.
Show Explanation

Written Explanation
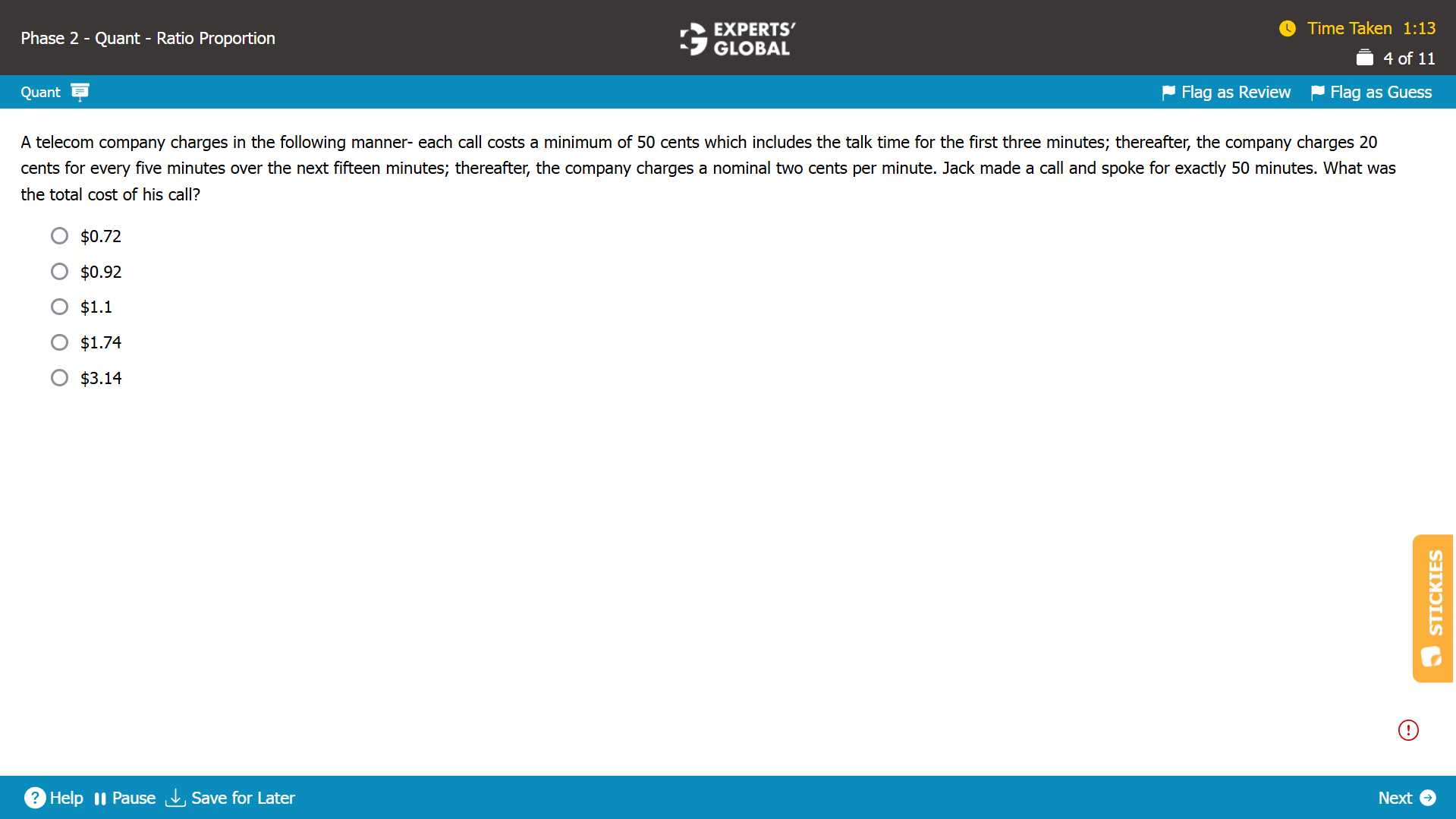
First three minutes: 50 cents
Next fifteen minutes: 20*15/5 = 60 cents
Last 32 minutes: 32*2 = 64 cents
Total cost: $1.74
Hence, D is the correct answer choice.
Show Explanation
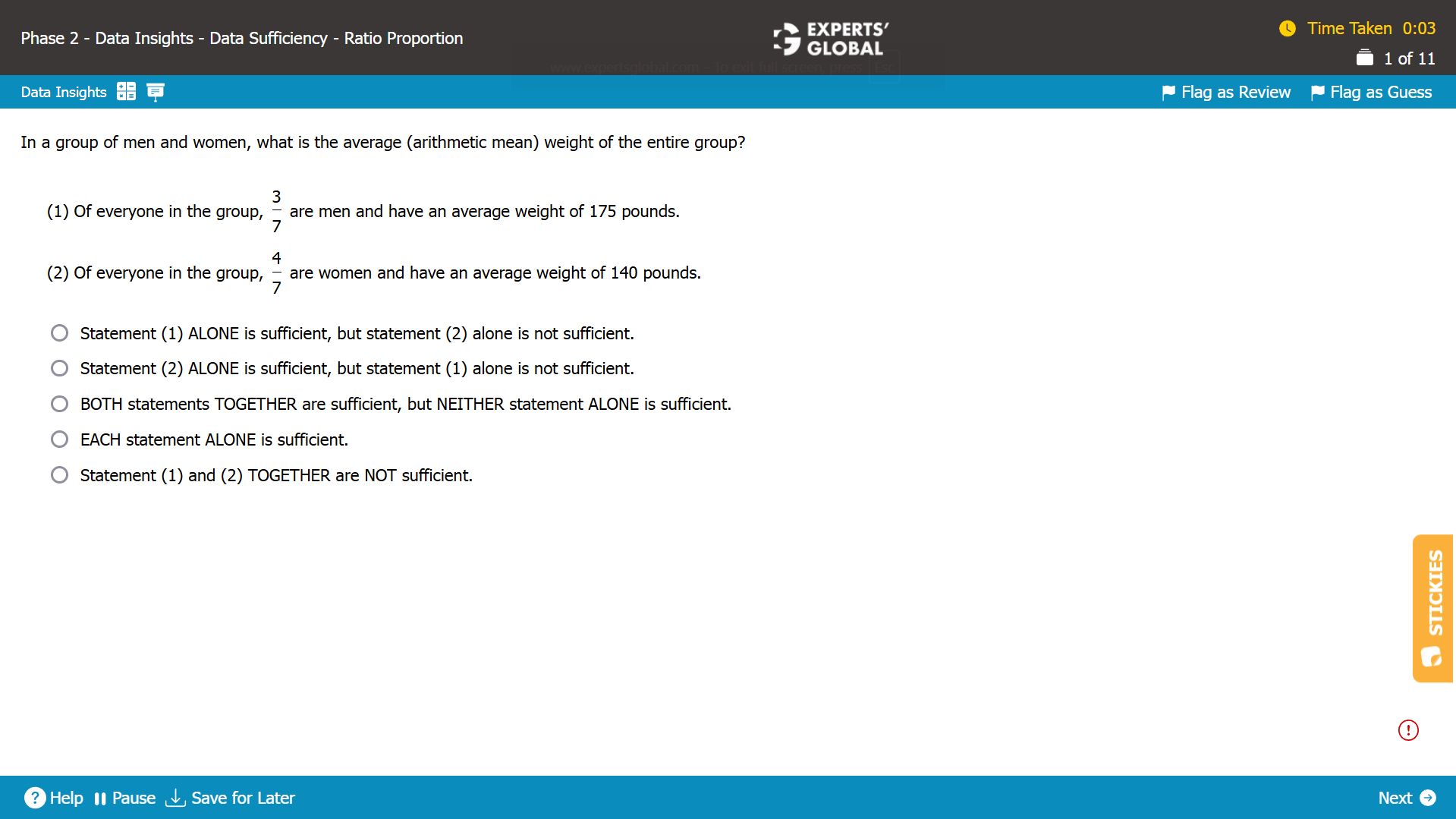
Let the total number of people in the group be N.
Average weight of the entire group = (Sum of all the weights)/N.
We need to find whether the value of (Sum of all the weights)/N can be determined.
Statement (1)
Number of men in the group = (3/7)N
The sum of the weights of all men = Average weight of men × Number of men in the group
The sum of the weights of all men = 175 × (3/7)N
It is NOT possible to determine the exact average weight of the entire group using the given information. Hence, Statement (1) is insufficient.
Statement (2)
Number of women in the group = (4/7)N
The sum of the weights of all women = Average weight of women × Number of women in the group
The sum of the weights of all women = 140 × (4/7)N
It is NOT possible to determine the exact average weight of the entire group using the given information. Hence, Statement (2) is insufficient.
As Statement (1) alone as well as Statement (2) alone is insufficient to answer the question, we need to now combine the two statements.
Statement (1) and Statement (2) combined
Average weight of the entire group
= (Sum of all the weights)/N
= (Sum of the weights of all men + Sum of the weights of all women)/N
= [175 × (3/7)N + 140 × (4/7)N]/N
= [175 × (3/7) + 140 × (4/7)]
It is possible to determine the exact average weight of the entire group. Hence, Statement (1) and Statement (2) combined are sufficient.
C is the correct answer choice.
Show Explanation
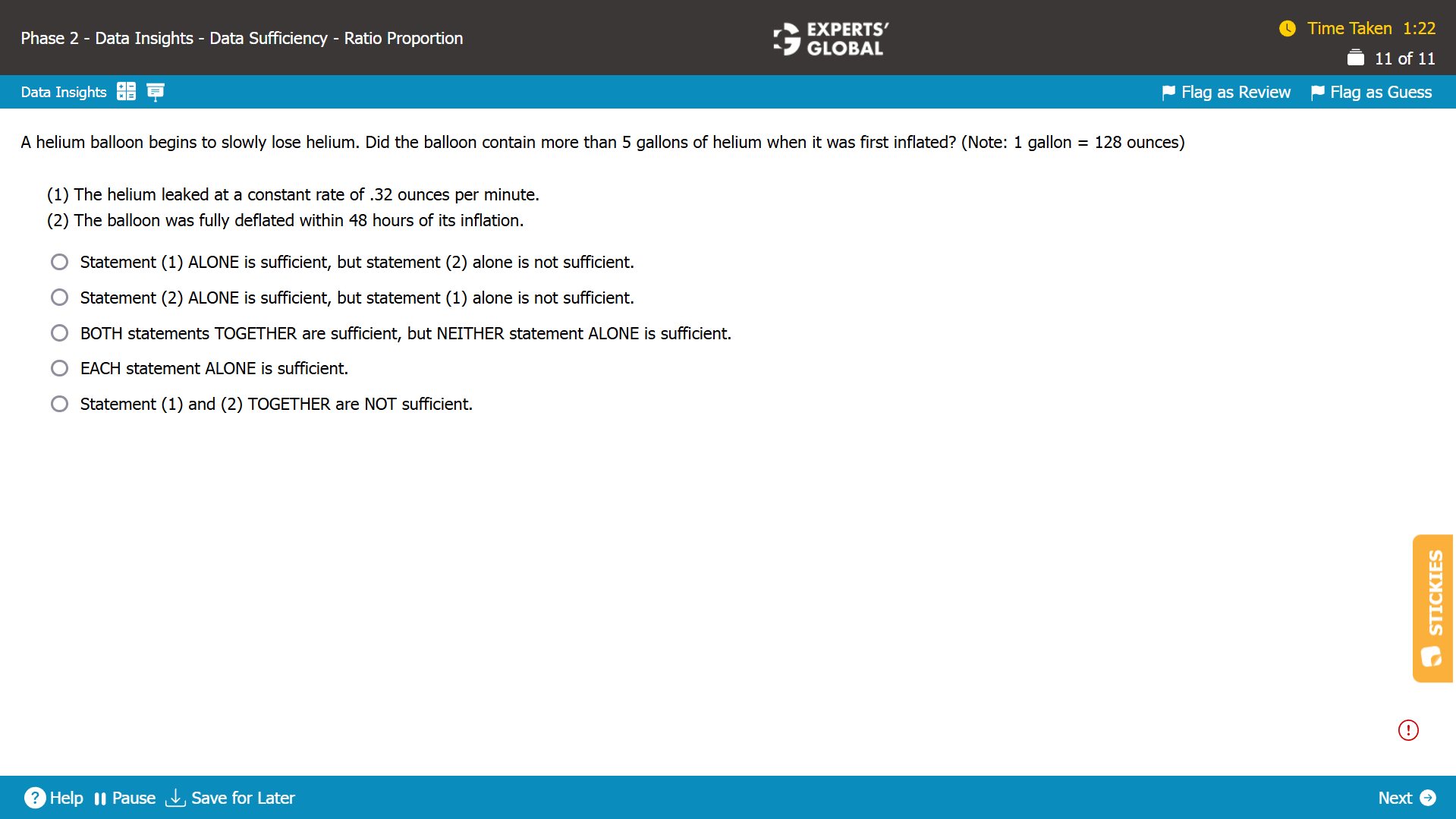
Let the time taken for the balloon to deflate be T.
Let the rate of helium leak be R.
Let the amount of helium in the balloon when it was first inflated be H.
We need to find whether H > 5 gallons.
Statement (1)
R = 0.32 ounces per minute
It is NOT possible to determine with certainty whether H is greater than 5 gallons. Hence, Statement (1) is insufficient.
Statement (2)
T < 48 hours.
It is NOT possible to determine with certainty whether H is greater than 5 gallons. Hence, Statement (2) is insufficient.
As Statement (1) alone as well as Statement (2) alone is insufficient to answer the question, we need to now combine the two statements.
Statement (1) and Statement (2) combined
R = 0.32 ounces per minute = [(0.32 × 60)/128] gallons per hour = 0.15 gallons per hour.
R × T = H
Possibility 1: If T = 10, then H = 0.15 × 10 = 1.5. In this case, H is NOT greater than 5 gallons.
Possibility 2: If T = 40, then H = 0.15 × 40 = 6. In this case, H is greater than 5 gallons.
It is NOT possible to determine with certainty whether H is greater than 5 gallons. Hence, Statement (1) and Statement (2) combined are insufficient.
E is the correct answer choice.
Show Explanation

Written Explanation
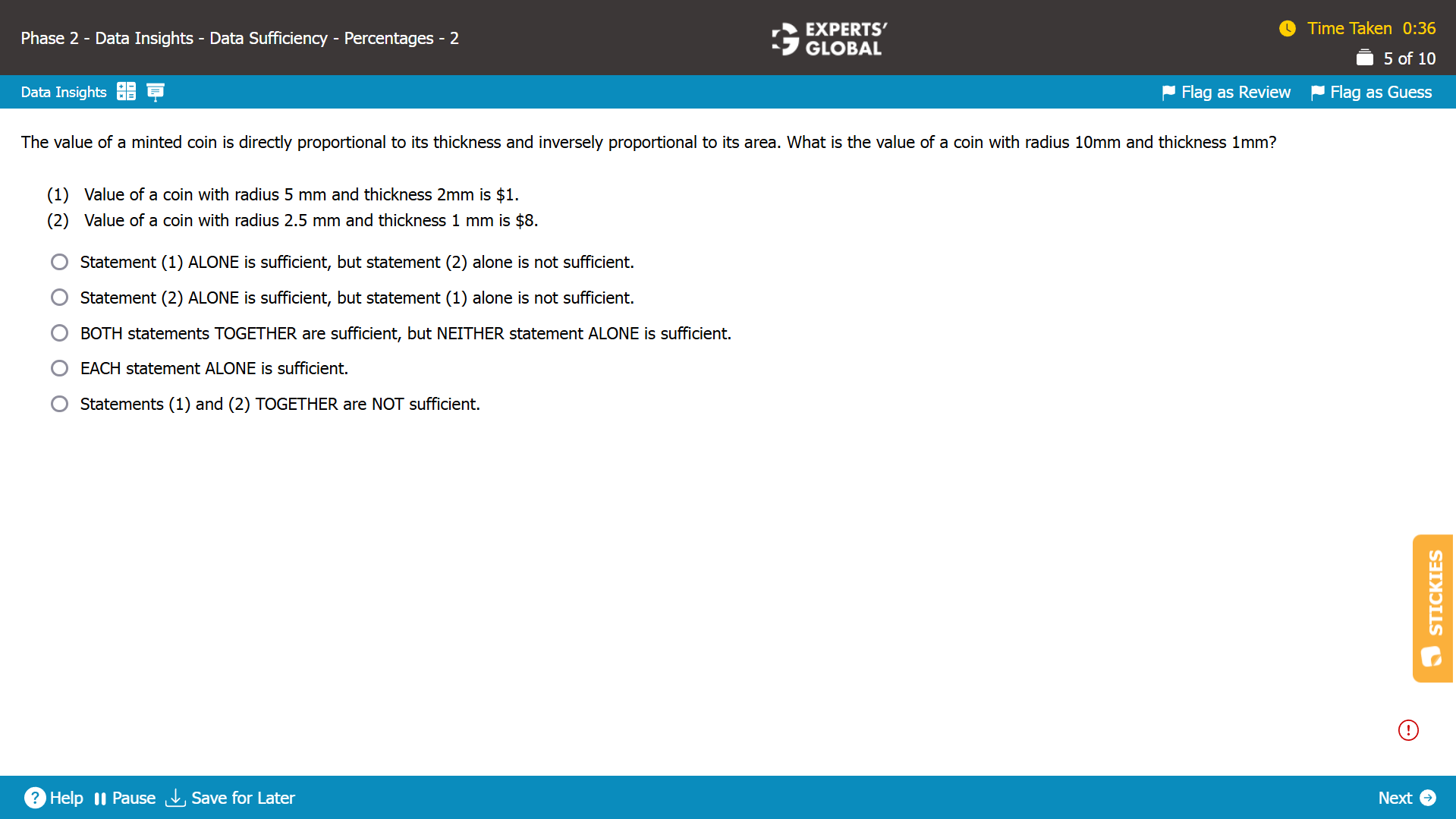
Let’s say that V is the value of a coin, T is the thickness of the coin, A is the area of the coin, and R is the radius of the coin.
The value is directly proportional to thickness and inversely proportional to area.
A coin is a circle. The area of a circle is directly proportional to the square of its radius.
Overall, V = K X T / R2 where K is a constant.
For the given coin, T = 10 and R = 1.
So, V = K X 10 / 12 = 10K needs to be determined.
Statement (1)
Value of a coin with radius 5 mm and thickness 2mm is $1.
1 = K X 5 / 22
The value of K can be determined.
10K can be determined.
The value of a coin with radius 10mm and thickness 1mm can be determined. Sufficient.
Statement (2)
Value of a coin with radius 2.5 mm and thickness 1 mm is $8.
8 = K X (2.5) / 12
The value of K can be determined.
10K can be determined.
The value of a coin with radius 10mm and thickness 1mm can be determined. Sufficient.
D is the correct answer choice.
Real practice for Ratio-Proportion-Variation problems begins when you solve them on a software simulation that closely matches the official GMAT interface. You need a platform that presents the question stem and the related information in a GMAT like layout, lets you work with the numbers and answer choices naturally, and provides all the on screen tools and functionalities that you will see on the actual exam. Without this kind of experience, it is difficult to feel fully prepared for test day. High quality Ratio-Proportion-Variation questions are not available in large numbers. Among the limited, genuinely strong sources are the official practice materials released by GMAC and the Experts’ Global GMAT course.
Within the Experts’ Global GMAT online preparation course, every Ratio-Proportion-Variation problem appears on an exact GMAT like user interface that includes all the real exam tools and features. You work through more than 100 Ratio-Proportion-Variation questions in quizzes and also take 15 full-length GMAT mock tests that include several Ratio-Proportion-Variation questions in roughly the same spread and proportion in which they appear on the actual GMAT.
All the best!