Invest 30 seconds...
...for what may lead to a life altering association!
Help Line
- +91.8800.2828.00 (IND)
- 1030-1830 Hrs IST, Mon-Sat
- support@expertsglobal.com
...for what may lead to a life altering association!


Functions describe how one quantity depends on another by assigning each input a single, well defined output, allowing us to study patterns, relationships, and changes in a clear and structured way. They form an important link between algebraic reasoning and real world situations. Careful coverage of this topic is an essential part of any comprehensive GMAT preparation course. This page offers you an organized subtopic wise playlist, along with a few worked examples, for efficient preparation of this concept.
Algebraic functions are among the most central ideas in mathematics, and on the GMAT they are often tested in ways that feel simple on the surface yet carry real depth. At heart, a function is just a rule that takes the variable x and replaces it with a specific input. The moment the input itself is another function, or when functions are applied repeatedly in composition, the work begins to reveal rich patterns. A single expression can unfold into a whole chain of transformations, which may look complicated, but the guiding idea stays unchanged: substitute the input faithfully and simplify with care. Growing comfortable with this steady, step by step substitution gives you the clarity required even for the more advanced questions. In the following short video, you will have the method explained, see how it works, and learn to apply it in GMAT drills, sectional tests, and full-length GMAT practice tests.

On the GMAT, function questions often check how accurately you can work with definitions rather than how fast you can calculate. Some function notations may seem unfamiliar at first, but once their meaning is clear, they become very approachable. The greatest integer and least integer functions, for instance, require close attention to wording, because they involve rounding values down or up in a specific manner. The factorial function, in contrast, simply represents the product of all positive integers from 1 up to a given number. While these ideas may initially look unusual, each follows a very simple, consistent pattern. The real key is to read the definition in the question carefully every single time. The following short video helps you see this concept in action and shows how it is tested on the GMAT.

On the GMAT, function questions often extend beyond single variables. At times, a function is defined in terms of both x and y, and you must substitute values for each before simplifying. This may feel like a major change at first, but the core idea remains unchanged: replace every variable with the given numbers carefully and move through the steps in order. The difficulty often increases with nested expressions, where the output of one function becomes the input of another. In such cases, accuracy depends on the discipline of working from the innermost expression outward. These problems quietly test your patience, your attention to detail, and your ability to apply definitions consistently. The brief video that follows turns this idea into something very clear and shows how it can appear on the GMAT.

One of the quieter ways in which the GMAT tests logical reasoning is through recursive functions, where each value of the function depends on the value that came before it. At first, such questions may seem puzzling because you cannot leap straight to the final answer. The right approach is to build the sequence one step at a time, using the given rule carefully. Each new value then opens the door to the next, until you finally reach the required term. This process is less about memorizing any formula and more about patiently applying the definition with full consistency. Recursive function questions reward discipline, clarity, and a methodical style of problem solving. Developing this mindset calls for practice with many different patterns, since the links between terms can vary widely. The short video below explains this concept in simple terms and demonstrates how the GMAT may test it.

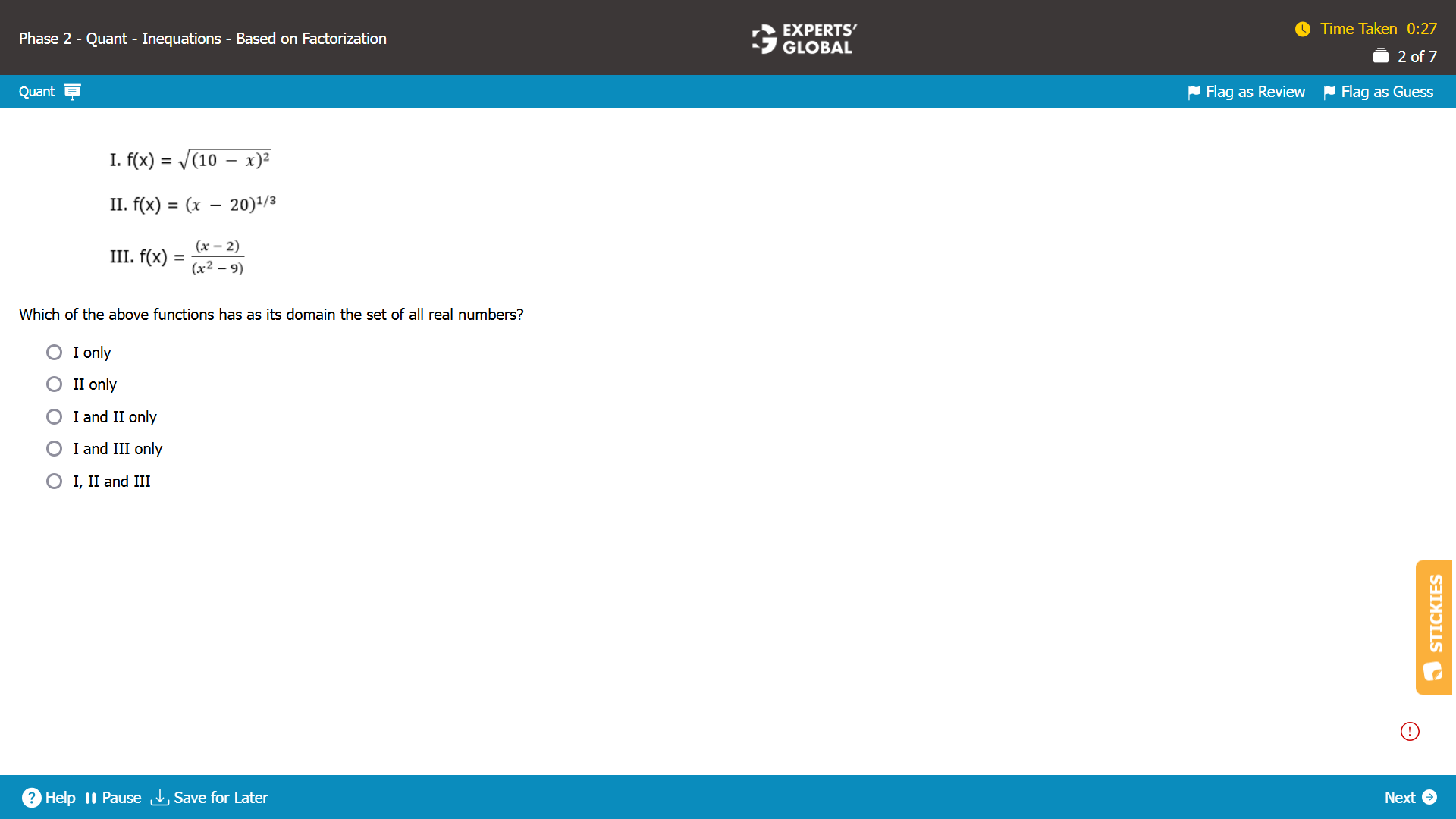
The domain of a function is the complete set of input values for which the function is defined. For example, if f(x) = x², you can use any real number, so the domain is all real numbers. If g(x) = 1 divided by x, you cannot divide by zero, so every real number except x = 0 belongs to the domain. In this lesson, you see domain as the set of real x values that keep a function defined and meaningful, and you learn how simple features such as denominators and square root signs quietly decide which inputs are allowed and which are excluded.



In this practice set, you will tackle a series of GMAT-style function questions, each accompanied by a carefully worked, stepwise explanation. Move through the problems at a calm pace and make a conscious effort to use the methods and ideas you have just studied on this page for handling function questions on the GMAT. At this stage, your main goal is to apply the strategy accurately and consistently, rather than to only arrive at the correct option. After attempting each question, use the explanation toggle to check the right answer and review the full descriptive reasoning.
Show Explanation
Show Explanation

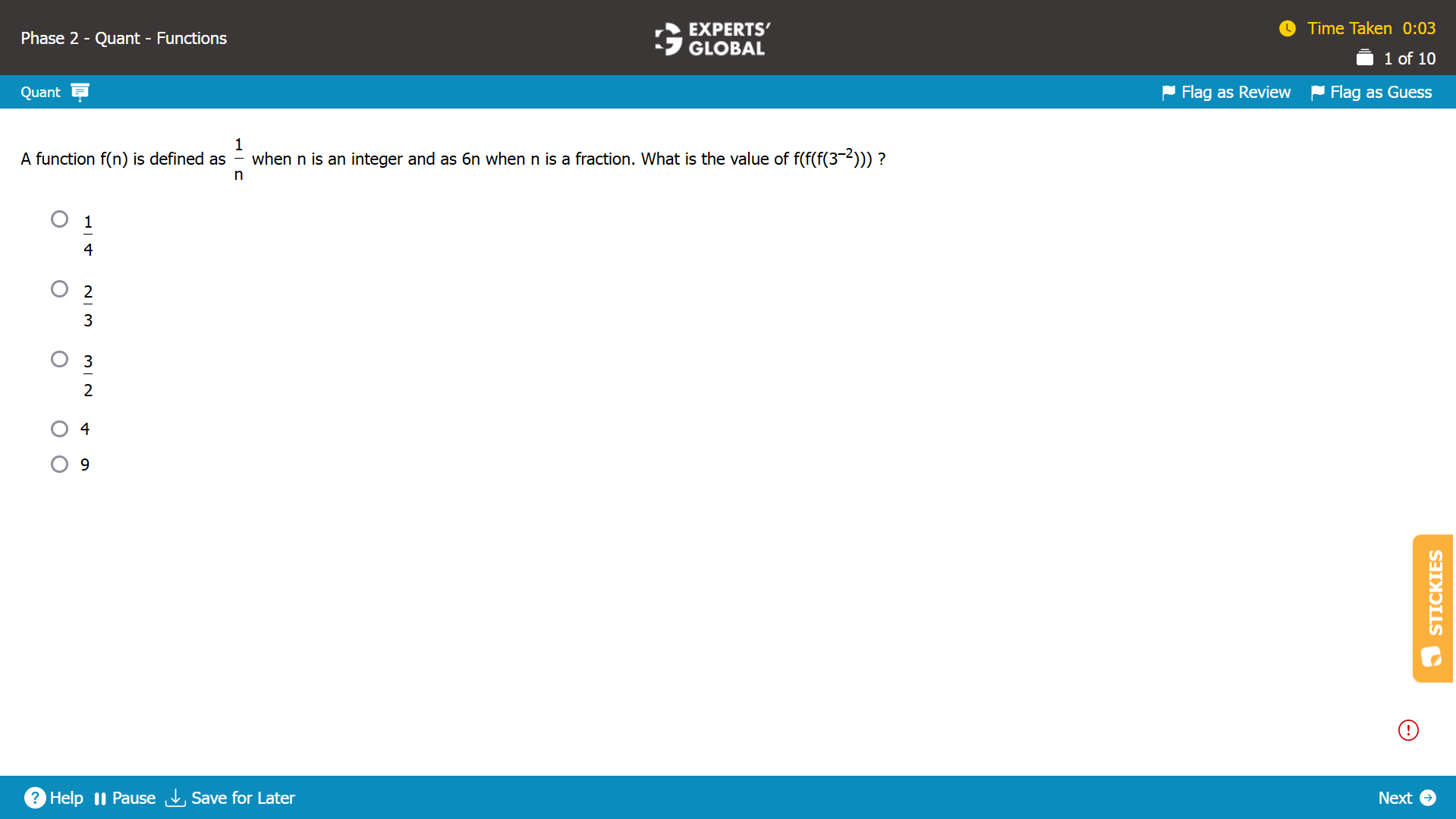
3–2 = 1 / 32 = 1 / 9; so, 3–2 is a fraction.
So, f(3–2) = 6 X (3–2) = 6 X (1 / 9) = 6 / 9 = 2 /3 is a fraction.
So, f(f(3–2)) = 6 X (2 / 3) = 4 is an integer.
So, f(f(f(3–2))) = 1 / 4.
A is the correct answer choice.
Show Explanation

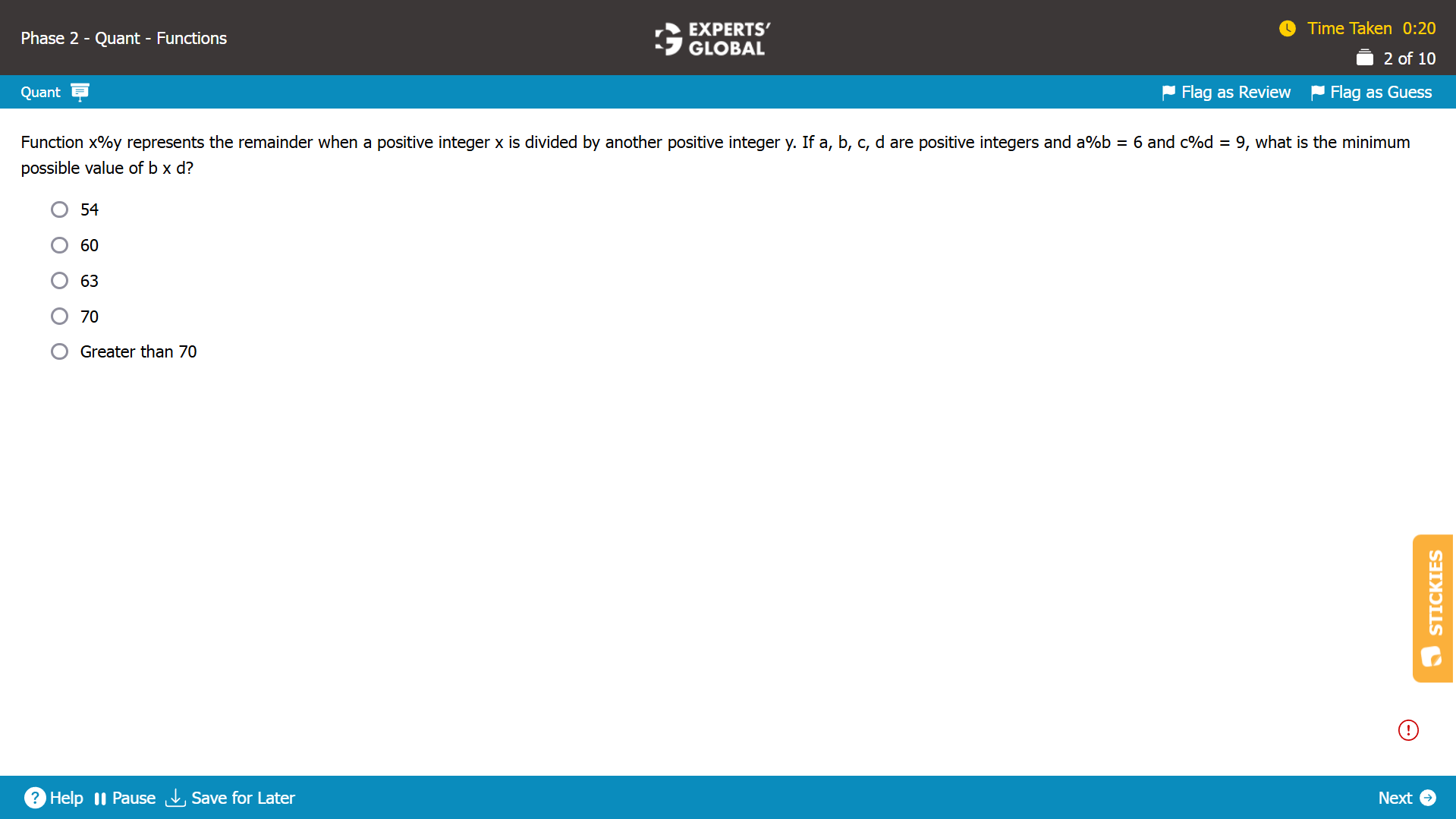
a%b = 6.
So, the remainder when a is divided by b is 6.
The remainder is always less than the divisor. So, the minimum possible value of b can be 6 + 1 = 7.
c%d = 9.
So, the remainder when c is divided by d is 9.
The remainder is always less than the divisor. So, the minimum possible value of d can be 9 + 1 = 10.
The minimum possible value of (b X d) = minimum possible value of b X minimum possible value of d = 7 X 10 = 70.
The minimum possible value of (b X d) is 70.
D is the correct answer choice.
Show Explanation

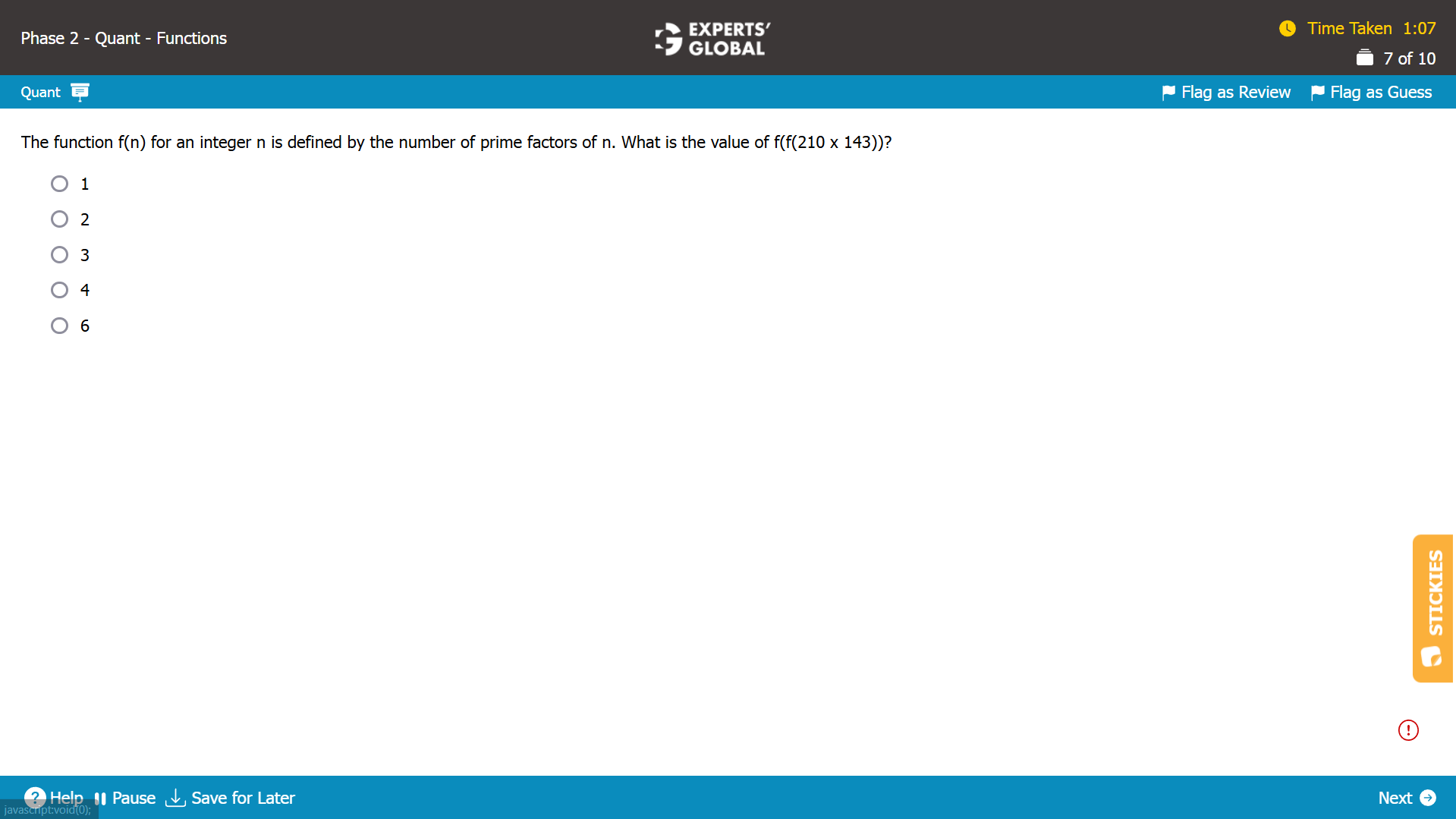
210 = 2 X 3 X 5 X 7.
143 = 11 X 13.
210 X 143 = 2 X 3 X 5 X 7 X 11 X 13.
(210 X 143) has 6 prime factors.
So, f(210 X 143) = 6.
6 = 2 X 3
6 has 2 prime factors.
So, f(6) = f(f(210 X 143)) = 2.
Overall, f(f(210 x 143)) = 2.
B is the correct answer choice.
Show Explanation

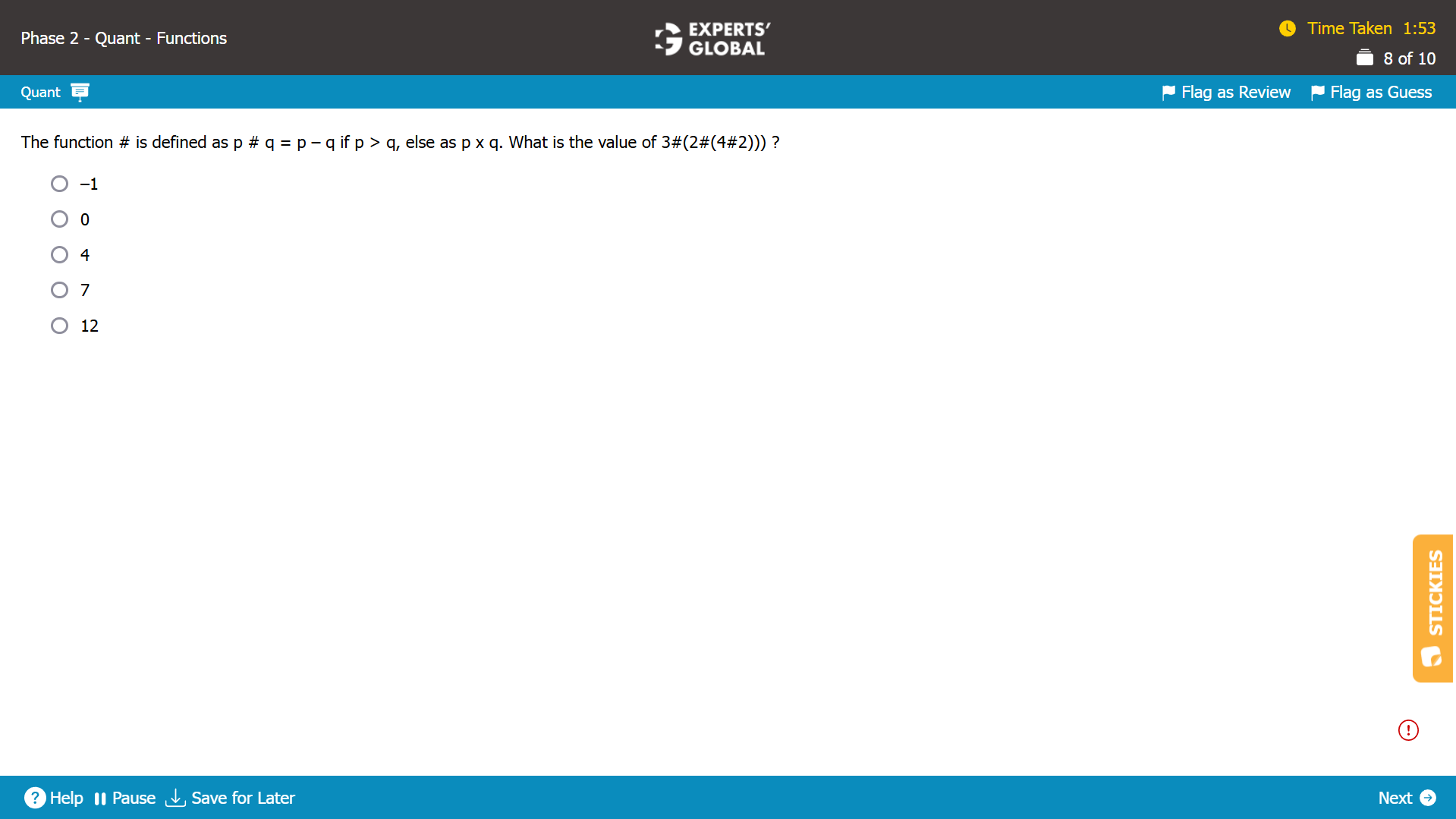
4 > 2.
So, 4#2 = 4 – 2 = 2.
2 = 2.
So, 2#2 = 2#(4#2) = 2 X 2 = 4.
3 < 4.
So, 3#4 = 3#(2#(4#2)) = 3 X 4 = 12.
Overall, 3#(2#(4#2))) = 12.
E is the correct answer choice.
Real practice for Functions problems begins when you solve them on a software simulation that closely matches the official GMAT interface. You need a platform that presents the question stem and the function definition or expression in a GMAT like layout, lets you work with the inputs, outputs, and answer choices naturally, and provides all the on screen tools and functionalities that you will see on the actual exam. Without this kind of experience, it is difficult to feel fully prepared for test day. High quality Functions questions are not available in large numbers. Among the limited, genuinely strong sources are the official practice materials released by GMAC and the Experts’ Global GMAT course.
Within the Experts’ Global GMAT online preparation course, every Functions problem appears on an exact GMAT like user interface that includes all the real exam tools and features. You work through more than 300 Functions questions in quizzes and also take 15 full-length GMAT mock tests that include several Functions questions in roughly the same spread and proportion in which they appear on the actual GMAT.
All the best!