Sequences describe ordered lists of numbers that follow a clear pattern, while series describe the sum of the terms in such lists. These ideas help students recognize structure, repetition, and growth in a very intuitive way. A good understanding of sequences and series is an essential part of any complete GMAT preparation course. This page offers you an organized subtopic wise playlist, along with a few worked examples, for efficient preparation of this concept.
Arithmetic Progression (AP)
Arithmetic progressions are both useful and graceful, and they appear regularly on the GMAT. In such a sequence, each term differs from the previous one by a fixed amount, forming the backbone of many well structured problems. If you master this idea early in your GMAT prep, it becomes a powerful ally, since its simplicity creates strong relationships that save valuable time. The skill to spot the nth term or find the total sum without adding term by term shows how crucial it is to recognize patterns quickly. The short video below explains this approach from first principles, shows it on GMAT like items, and prepares you to use it in drills, sectional tests, and full-length GMAT diagnostic tests.
Arithmetic Progression on GMAT
Geometric Progression (GP)
Geometric progressions form a key part of sequences and series, and they often sit at the heart of elegant GMAT problems. In a geometric progression, each term is produced by multiplying the previous term by a constant ratio. Unlike arithmetic progressions, which increase by repeated addition, geometric progressions grow or shrink through multiplication, creating patterns that rise sharply or fade quickly. Their real strength lies in the formulas that allow you to find the nth term, the sum of a fixed number of terms, and even the sum of infinitely many terms under certain conditions. These relationships let you manage very large terms and complicated looking series without writing out every term. A solid grasp of these formulas, along with the reasoning behind them, saves time and cuts down on errors. The following short video presents this idea step by step and shows how it can be tested on the GMAT.
Geometric Progression on GMAT
Summation formulas are some of the most elegant and powerful tools in mathematics. Rather than adding terms one by one, these relationships let you reach the final sum in a single, confident step. On the GMAT, questions involving sums of consecutive integers, even numbers, odd numbers, or powers can look long and tiring if handled manually. With the right formulas, though, they become crisp and efficient. For instance, the sum of the first n natural numbers, or the first n squares, can be found in moments once you know the underlying patterns. These ideas are not only about saving time; they are about recognizing structure where others see only repetition. That is why regular practice with these formulas is essential for true fluency. The brief video that follows gives a warm, clear explanation of this idea and shows how it can show up on the GMAT.
Summation Formulas: Sum of n Integers, Squares, Cubes on GMAT
GMAT-style GMAT Sequences and Series Questions with Explanations
In this section, you will work through a carefully selected set of GMAT-style Sequences and Series questions, each followed by a clear, stepwise explanation. Move through the problems steadily and make a deliberate effort to apply the ideas and techniques you have just studied on this page for solving Sequences and Series questions on the GMAT. At this stage, give more weight to using the structured approach correctly than to simply reaching the right answer. After finishing a question, open the explanation panel to check the correct response and review the reasoning in detail.
Practice Question 1
Written Explanation
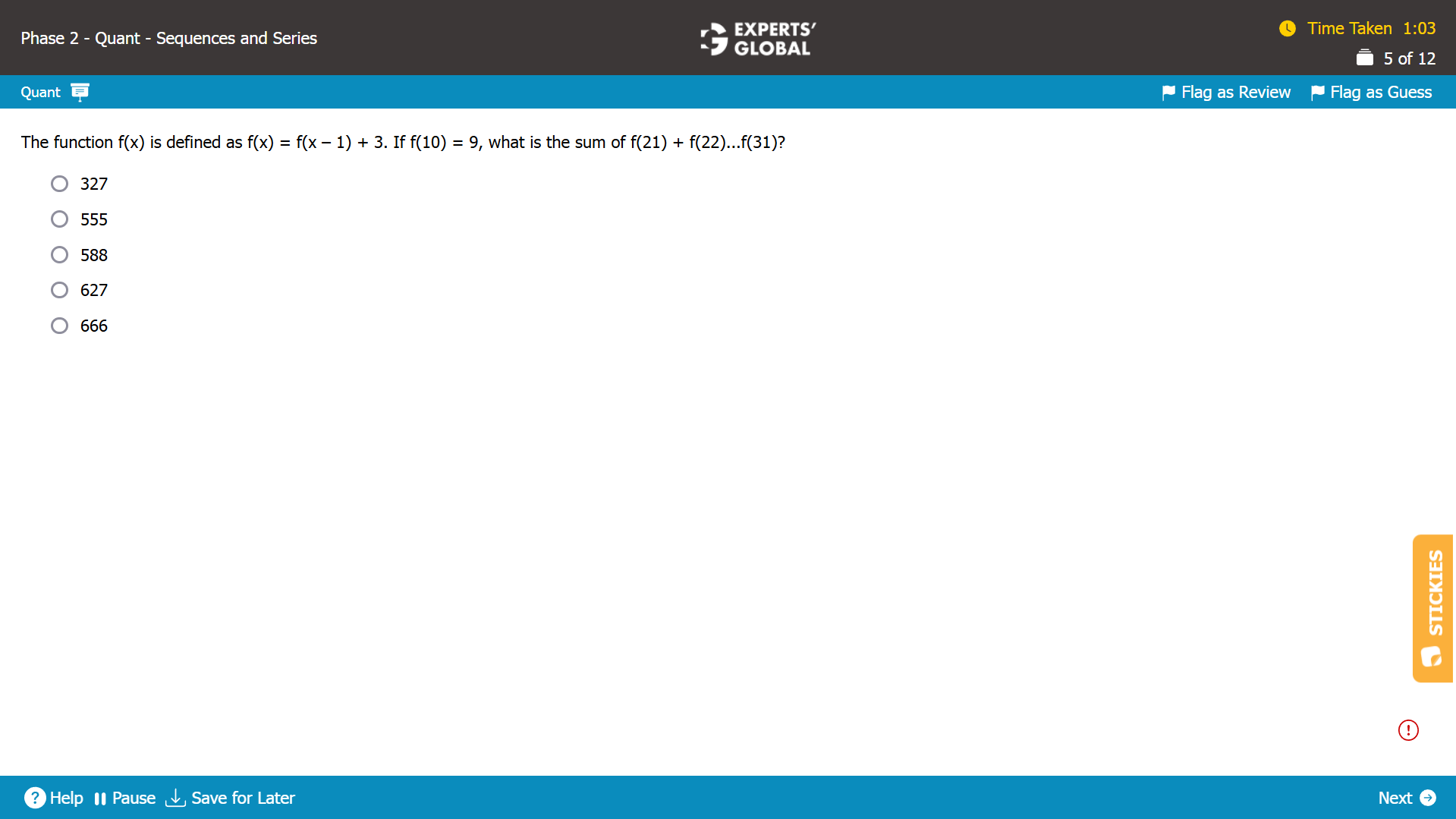
f(x) = f (x – 1) + 3
So, if f(1), f(2), f(3)….are arranged in order, they will have 3 as the common difference; in other words, the function represents an arithmetic progression.
f(10) = 9.
f(21) will be 21 – 10 = 11 terms ahead of f(10); so f(21) = f(10) + 11 X 3 = 9 + 33 = 42.
f(31) will be 31 – 10 = 21 terms ahead of f(10); so f(31) = f(10) + 21 X 3 = 9 + 63 = 72.
There are 31 – 21 + 1 = 11 terms between f(21) and f(31), both inclusive.
When the first and the last terms of an arithmetic profession are given,
Sum of all the terms between the first and the last terms, both inclusive = (number of terms / 2) X (first term + last term)
f(21) + f(22)…f(31) = (11 / 2) X ( 42 + 72) = 627.
D is the correct answer choice.
Practice Question 2
Written Explanation
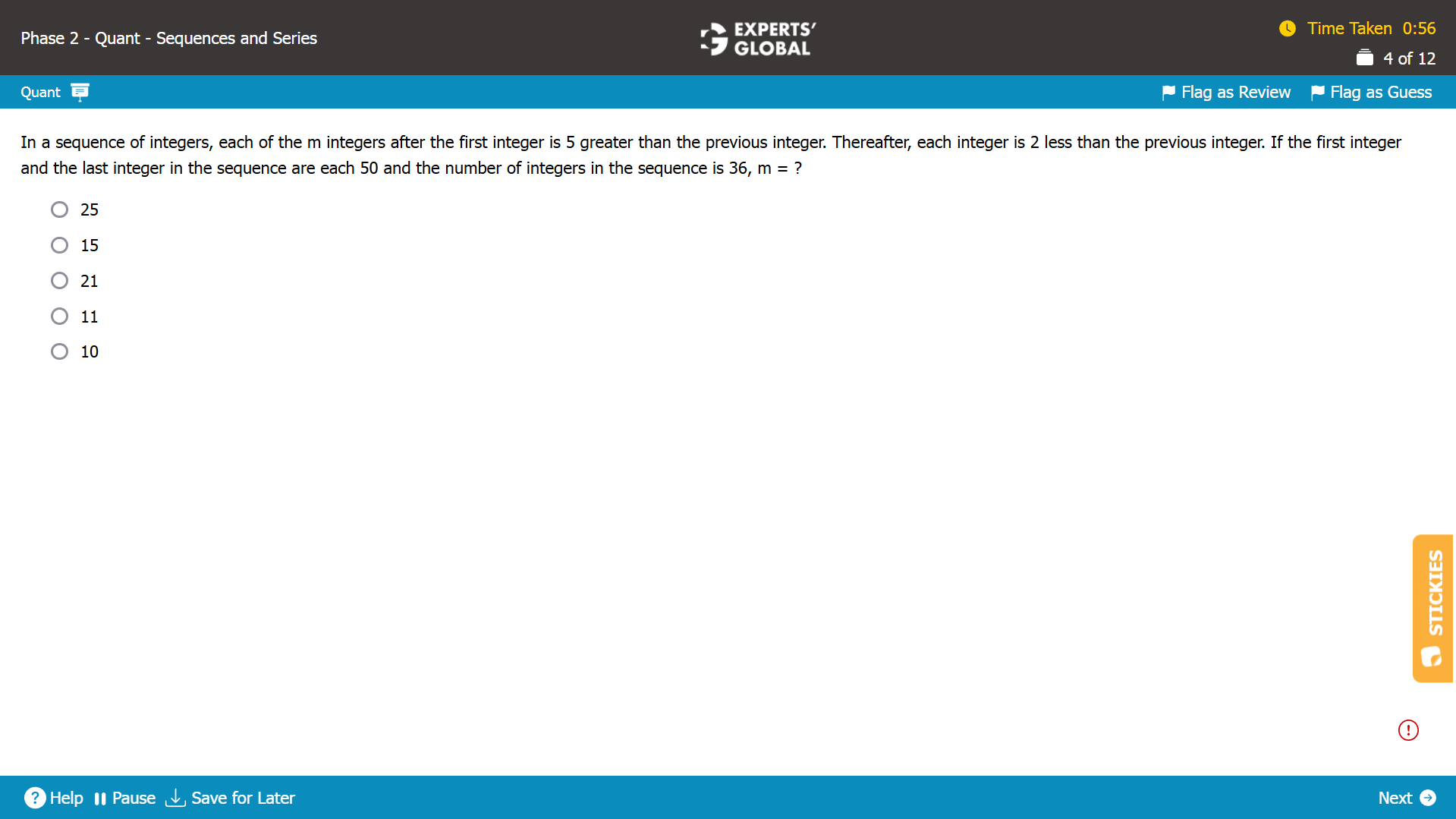
Let’s say that the first integer is x.
For the next m integers, the difference between any consecutive integers is 5.
So, the set, when arranged in ascending order is {x, x + 5, x + 10…. x + 5m…}.
After the first (m + 1) terms, until the 36th term in the series, the difference is –2.
So, the set, when arranged in ascending order is {x, x + 5, x + 10…. x + 5m, x + 5m – 2, x + 5m – 4 ….until the 36th term}.
The first and the last terms are 50. So, the set is….
{50, 55, 60…. 50 + 5m, 50 + 5m – 2, 50 + 5m – 4 ….50}.
It can be inferred that..
The values in the set increase by 5 for m terms, or until the (m + 1)th term.
The values in the set decrease by 2 for 36 – (m + 1) = (35 – m) terms.
The net change from the first to the last term is zero.
So,
5m – 2 X (35 – m) = 0
7m = 70
m = 10
E is the correct answer choice.
Practice Question 3
Written Explanation
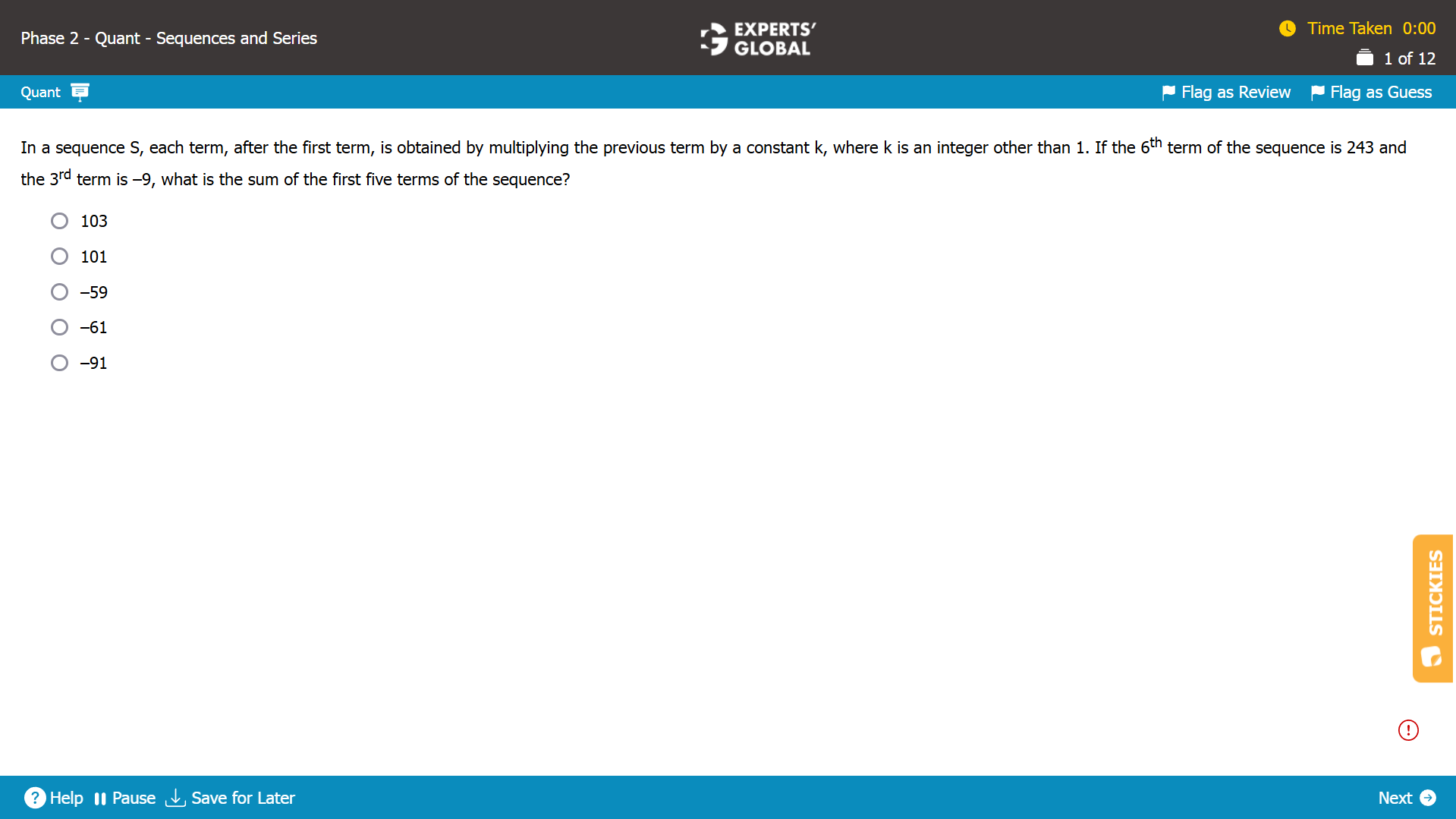
Each next term in the sequence is obtained by multiplying the previous term by a constant. So, the sequence is in geometric progression.
Let’s say that the first term in the set is x.
The second term would be xk.
The third term would be xk2 = –9…. (Equation I)
Similarly, the sixth term will be x X (k)5 = 243…. (Equation II)
Substituting Equation I in Equation II
(–9) X k3 = 243
k = –3
Substituting k = –3 in Equation I…
x (–3)2 = –9
x = –1
The first term of the sequence = –1
The second term of the sequence = (–1) X (–3) = 3
The third term of the sequence = (3) X (–3) = –9
The fourth term of the sequence = (–9) X (–3) = 27
The fifth term of the sequence = (27) X (–3) = –81
The sum of the first five terms will be (–1) + (3) + (–9) + (27) + (–81) = –61.
D is the correct answer choice.
Practice Question 4
Written Explanation
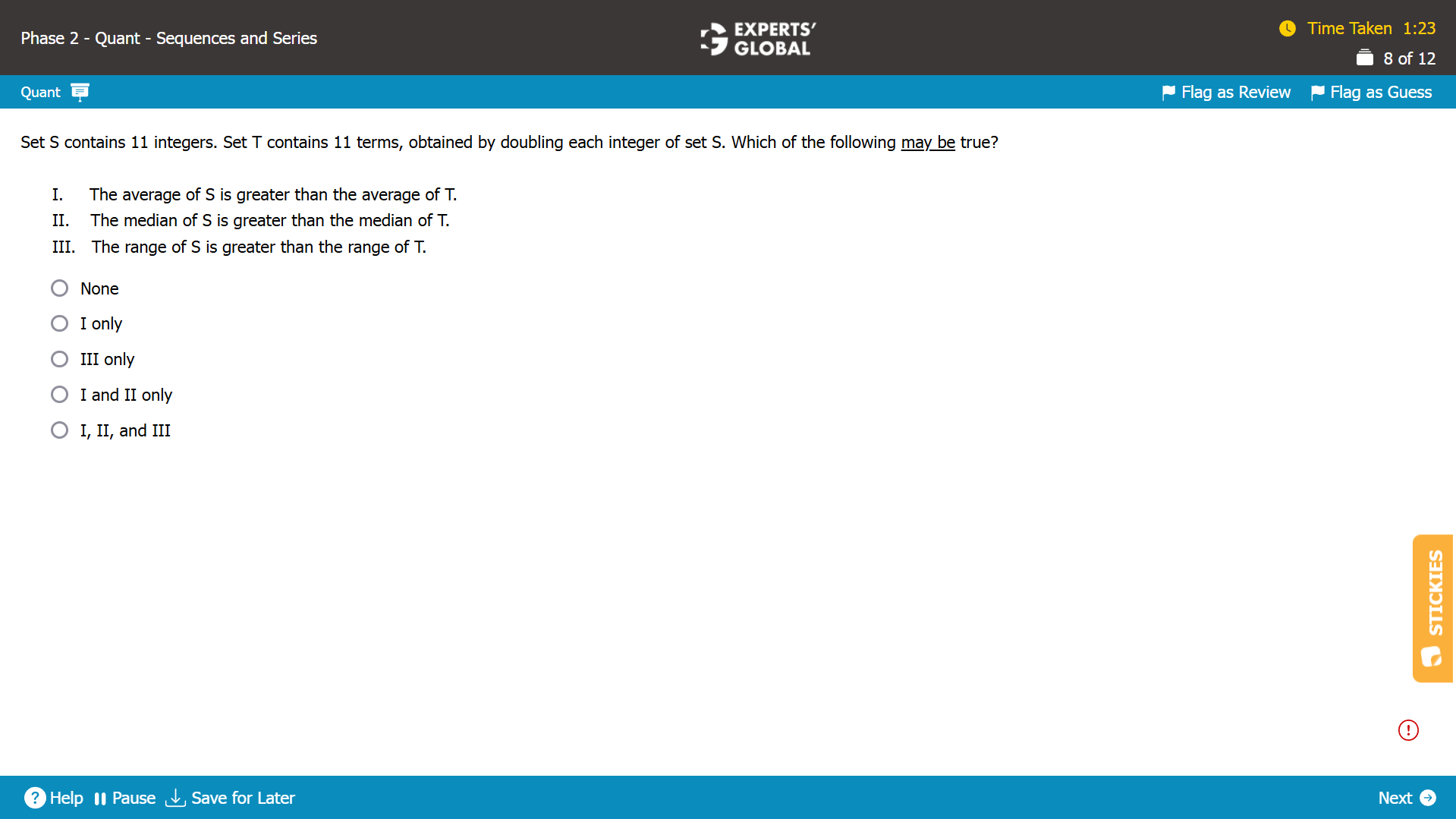
Let’s say that that set S is in arithmetic progression.
Possibility 1:
S = {–1, –2, –3, –4,….–11} with mean = median = 6th term = –6.
and
T = {–2, –4, –6, –8,….–22} with mean = median = 6th term = –12.
The average of S is greater than the average of T. Statement I MAY BE TRUE.
Possibility 2:
S = {–1, –2, –3, –4,….–11} with mean = median = 6th term = –6.
and
T = {–2, –4, –6, –8,….–22} with mean = median = 6th term = –12.
The median of S is greater than the median of T. Statement II MAY BE TRUE.
Possibility 3:
S = {a, a + d, a + 2d,….a + 10d } with range = (a + 10d ) – a = 10d.
and
T = {2a, 2a + 2d, 2a + 4d,….2a + 20 } with range = (2a + 20d ) – 2a = 20d.
The range of S will always be half of the range of T. Statement III WILL NEVER BE TRUE.
D is the correct answer choice.
Practice Question 5
Written Explanation
Let’s say that Lily makes a red mark at the bottom of the ring, as shown.
Firstly, Lily puts a green mark at every 72 degrees angle from the center. There would be 360 / 72 = 5 marks.
The first green mark would be at 72 degrees from the red mark, as shown.
The second green mark would be at 72 + 72 = 142 degrees from the red mark, as shown.
The third green mark would be at 144 + 72 = 216 degrees from the red mark, as shown.
The fourth green mark would be at 216 + 72 = 288 degrees from the red mark, as shown.
The fifth green mark would be at 288 + 72 = 360 degrees from the red mark. So, the fifth green mark would coincide with the red mark.
Secondly, Lily puts a blue mark at every 45 degrees angle from the center. There would be 360 / 45 = 8 marks.
The first blue mark would be at 45 degrees from the red mark, as shown.
The second blue mark would be at 45 + 45 = 90 degrees from the red mark, as shown.
The third blue mark would be at 90 + 45 = 135 degrees from the red mark, as shown.
The fourth blue mark would be at 135 + 45 = 180 degrees from the red mark, as shown.
The fifth blue mark would be at 180 + 45 = 225 degrees from the red mark, as shown.
The sixth blue mark would be at 225 + 45 = 270 degrees from the red mark, as shown.
The seventh blue mark would be at 270 + 45 = 315 degrees from the red mark, as shown.
The eighth blue mark would be at 315 + 45 = 360 degrees from the red mark. So, the eighth blue mark would coincide with the red mark.
Overall, the marks are at {0, 45, 72, 90, 135, 144, 180, 216, 225, 270, 288, 315} degrees from the red mark.
When the ring is cut at these marks, the unique sizes would be as follows.
When a cut is made at 0 degrees, the first cut is made in the ring.
When a cut is made at 45 degrees, a piece representing 45 – 0 = 45 degrees is made. This piece is unique; so, it is removed.
When a cut is made at 72 degrees, a piece representing 72 – 45 = 27 degrees is made. This piece is unique; so, it is removed.
When a cut is made at 90 degrees, a piece representing 90 – 72 = 18 degrees is made. This piece is unique; so, it is removed.
When a cut is made at 135 degrees, a piece representing 135 – 90 = 45 degrees is made. This piece is NOT unique; so, it is NOT removed.
When a cut is made at 144 degrees, a piece representing 144 – 135 = 9 degrees is made. This piece is unique; so, it is removed.
When a cut is made at 180 degrees, a piece representing 180 – 144 = 36 degrees is made. This piece is unique; so, it is removed.
When a cut is made at 216 degrees, a piece representing 216 – 180 = 36 degrees is made. This piece is NOT unique; so, it is NOT removed.
When a cut is made at 225 degrees, a piece representing 225 – 216 = 9 degrees is made. This piece is NOT unique; so, it is NOT removed.
When a cut is made at 270 degrees, a piece representing 270 – 225 = 45 degrees is made. This piece is NOT unique; so, it is NOT removed.
When a cut is made at 288 degrees, a piece representing 288 – 270 = 18 degrees is made. This piece is NOT unique; so, it is NOT removed.
When a cut is made at 315 degrees, a piece representing 315 – 288 = 27 degrees is made. This piece is NOT unique; so, it is NOT removed.
Overall, the pieces that are removed represent 45 + 27 + 18 + 9 + 36 = 135 degrees.
135 degrees represent 135 / 360 = 37.5% of the circle.
Approximately 38% of the original ring was removed.
B is the correct answer choice.
How and Where to Practice GMAT Sequences and Series Questions
Real practice for Sequences and Series problems begins when you solve them on a software simulation that closely matches the official GMAT interface. You need a platform that presents the question stem and the sequence or series framework in a GMAT like layout, lets you work with the information and answer choices naturally, and provides all the on screen tools and functionalities that you will see on the actual exam. Without this kind of experience, it is difficult to feel fully prepared for test day. High quality Sequences and Series questions are not available in large numbers. Among the limited, genuinely strong sources are the official practice materials released by GMAC and the Experts’ Global GMAT course.
Within the Experts’ Global GMAT online preparation course, every Sequences and Series problem appears on an exact GMAT like user interface that includes all the real exam tools and features. You work through more than 40 Sequences and Series questions in quizzes and also take 15 full-length GMAT mock tests that include several Sequences and Series questions in roughly the same spread and proportion in which they appear on the actual GMAT.
All the best!
