Inequations – Based on Factorization (Wavy Curve Method) on GMAT

Quick Summary

Polynomial inequalities simplify once you factorize, identify critical points, and test sign changes across intervals. Using a number line helps track positivity and negativity. This structured method, called the wavy curve method, avoids confusion, saves time, and ensures accuracy on factorization-based GMAT inequality questions.

Overview

Polynomial inequalities often look intimidating because of their large expressions, but the underlying concept is logical and systematic. The GMAT does not usually test very large expressions, but building clarity on such examples ensures that even the trickiest cases become simple to handle. The key lies in factorization and analyzing the behavior of the polynomial across its critical points. In your GMAT prep, once you learn to mark these points, represent them on a number line, and understand how the signs alternate, the question reduces to an elegant exercise in logic rather than a heavy calculation. It is called the wavy curve method and is truly efficient solving the factorization based inequalities on GMAT.

This clarity is important because since inequalities form the backbone of higher-level problem solving. If you wish to build speed and accuracy, make sure you also revise how polynomials behave across intervals by solving a high volume of GMAT practice questions, in GMAT drills as well as GMAT full-length mocks.

 

Understanding Polynomial Inequalities: The Wavy Curve Method

Polynomial inequalities ask whether a given polynomial expression is positive or negative for certain values of x. For example:

An Explanatory Question:
For what values of x, is (x – 2)(x – 3)(x + 6)(x + 5) > 0

At first glance, the expression looks complex, but the structured approach makes it manageable.

Step 1: Factorization and Nodes

The given expression is already factorized: (x – 2)(x – 3)(x + 5)(x + 6).
Now, equating each term to zero gives the critical values or nodes: x = 2, 3, –5, –6. At these points, the polynomial becomes zero.

Step 2: Represent the Nodes on the Number Line

Mark –6, –5, 2, and 3 on a number line. These values divide the number line into intervals. In each interval, the sign of the polynomial can be determined by checking the number of negative terms.

 

Step 3: Analysing Signs Across Intervals

• For x > 3: All four terms are positive, so the polynomial is positive.
• For 2 < x < 3: Three terms are positive, one is negative, so the result is negative.
• For –5 < x < 2: Two negatives and two positives give a positive product.
• For –6 < x < –5: Three negatives and one positive give a negative product.
• For x < –6: All four terms are negative, and the product is positive.

Step 4: Interpreting the Solution

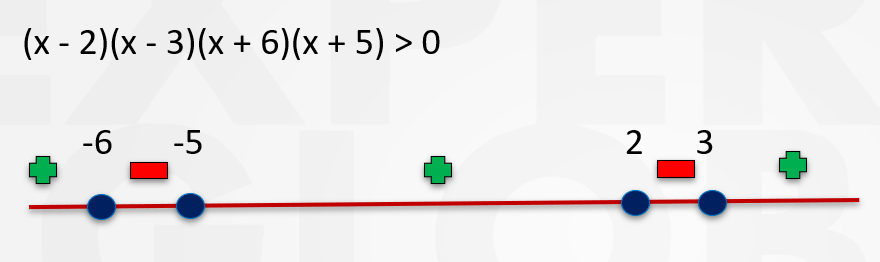
Since the inequality requires the polynomial to be positive, the valid ranges are: x > 3, –5 < x < 2, or x < –6.

Shortcut Tip

To save time, remember that the rightmost region (x greater than the largest node) will always be positive. From there, alternate the sign across each interval as you move leftward.

Additional Example

For what values of x is  (x)(x – 1)(x – 6) < 0?

The nodes are 0, 1, and 6.

Start with x > 6, where the sign is positive, and alternate leftward.

The pattern becomes positive – negative – positive – negative.

Since the question asks for negative values, the valid ranges are 0 < x < 1 and 1 < x < 6.

Final Thought

Polynomial inequalities reward clarity and structure more than brute calculation. Always factorize, mark the nodes, alternate the signs, and interpret the ranges with confidence. With this approach, you will never feel lost when facing such problems in GMAT  Quantitative Reasoning. You may want to see such examples as part of a GMAT test by taking a free GMAT full-length mock test.

Parting Thought

Factorizing an inequality teaches a discipline: locate the turning points, map the intervals, and let signs reveal truth without noise. In GMAT preparation, do the same, identify core ideas, mark their boundaries, and practice until patterns alternate clearly in your mind. In the MBA application stage, know your critical points: values, achievements, and goals. Arrange them in order, then choose the ranges that express you faithfully. In life, progress often emerges when you find where you stand, where you do not, and why. Clarity is the courage to draw lines with kindness and to act with structure, patience, and purpose.