Invest 30 seconds...
...for what may lead to a life altering association!
Help Line
- +91.8800.2828.00 (IND)
- 1030-1830 Hrs IST, Mon-Sat
- support@expertsglobal.com
...for what may lead to a life altering association!


Derangements are special permutations where no element stays in its original place. For example, with four letters and envelopes, a derangement ensures no letter matches its envelope. For n = 4, the total number of derangements is 9, illustrating restricted arrangement logic.
Did you know? Thousands of students find our mocks closely match the GMAT. Take your first GMAT mock free!
Derangements are permutations in which no element appears in its original position, a key concept in combinatorics. This article and the accompanying video explain the idea through structured examples, beginning with four letters and envelopes and exploring each possible case. From the impossibility of three correct matches to the exact values of D(n) for small n, the discussion builds clarity step by step. The general formula is then introduced, along with applications where some elements are fixed and others deranged. Since such restricted arrangements form part of advanced counting, they deserve a place in a thorough GMAT prep course, ensuring that students grasp both method and reasoning.

Derangements are a special type of permutation in which no element remains in its original position.
Mathematically, the number of derangements of n objects is given by D(n) = n! × (1 – 1/1! + 1/2! – 1/3! + … + (–1)ⁿ / n!).
This alternating factorial expression captures the logic of eliminating fixed positions from ordinary arrangements.
Three books are to be placed on three distinct shelves, but none can go back to its original shelf. How many valid arrangements are possible?
If the first book avoids its original shelf, it has two options.
Whichever option is chosen, the remaining two books will be forced into specific positions where neither can remain in its original place.
Checking both possibilities shows that exactly 2 valid arrangements exist.
Using the formula for n = 3:
D(3) = 3! × (1 – 1/1! + 1/2! – 1/3!)
= 6 × (1 – 1 + 0.5 – 0.166…)
= 6 × (0.333…)
= 2
So, there are exactly 2 derangements for three objects.
Question: 4 letters are randomly put in 4 envelopes. How many unique cases are possible such that…
No letter goes into right envelope?
This is only possible in one way.
Every letter is placed correctly.
So, the answer is simply 1.
This case is impossible.
If three letters are correct, the fourth is automatically correct as well, contradicting the condition.
Hence, the answer is 0.
Here, we must choose which two letters go correctly.
That can be done in 4C2 = 6 ways.
The remaining two letters are forced into the wrong positions, leaving exactly one arrangement.
So, the answer is 6.
Select the correct letter in 4 ways.
Now, three letters remain.
These three can be deranged in 2 ways.
Thus, the answer is 4 × 2 = 8.
This is a perfect derangement.
For n = 4, the number of derangements is D(4).
Using the formula, D(4) = 9.
Generally, large values are not asked on the GMAT, because the test is logic-based and not complex mathematics/formula-driven.
The number of derangements of n elements, D(n), is given by:
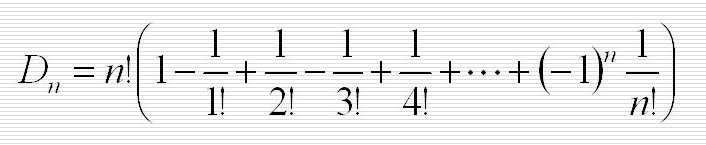
This alternating series helps calculate derangements efficiently.
These are more than enough for test purposes, as larger values rarely appear.
Choose the correct one in 5C1 = 5 ways, then derange the remaining four.
Therefore, 5C1 × D(4)
Answer = 5 × 9 = 45.
Select two correct letters in 6C2 = 15 ways, then derange the remaining four.
Therefore, 6C2 × D(4)
Answer = 15 × 9 = 135.
Derangements provide an elegant way to deal with restricted permutations. They are not only about letters and envelopes but also apply to seating, assignments, and many distribution problems. The key is to identify when the condition “no element remains in its original place” or “exactly k elements are in the correct place” appears in the problem
Derangements highlight the beauty of combinatorics by showing how order can be restructured under strict restrictions. From small cases like three or four objects to larger applications involving seating and assignments, the logic emphasizes precision in counting. Mastering this concept develops not only formula fluency but also logical flexibility, both essential for advanced problem solving. Because topics like derangements are rare but conceptually deep, practicing them refines reasoning skills and enhances confidence under time limits. Including such problems in your GMAT mocks ensures that your preparation remains comprehensive and sharp, ready for unexpected twists on test day.
Derangements remind us that life does not always follow expected positions. Success often lies in adapting when nothing is in its original place. In GMAT preparation, too, comfort with the unfamiliar and disciplined practice build the resilience to handle surprises on test day. The B-school applications similarly demand flexibility: essays, interviews, and recommendations rarely align perfectly, yet clarity of thought brings order to the seeming disorder. Beyond academics, life presents countless derangements where plans do not match outcomes. The ability to restructure calmly and think creatively often defines achievement far more than perfect alignment ever could.