Invest 30 seconds...
...for what may lead to a life altering association!
Help Line
- +91.8800.2828.00 (IND)
- 1030-1830 Hrs IST, Mon-Sat
- support@expertsglobal.com
...for what may lead to a life altering association!


Areal probability is the chance of an event occurring when outcomes are spread across an area. It is the ratio of favorable area to total area. For example, if a dartboard is half red and half blue, hitting red has probability 1/2.
Targeting ISB? Check our ISB admission consulting service!
Areal probability is one of the most intuitive forms of probability, because it connects abstract concepts to simple geometry. The idea is that probability can be seen as a fraction of areas: the favourable region divided by the total region. GMAT questions based on this principle may involve elementary geometry or coordinate geometry, where a condition such as a point lying inside a triangle or x greater than y defines the favourable region. The challenge is not heavy calculation but clear visualization of the diagram and recognition of the boundaries. Once this is done, the required probability becomes a ratio of areas that can often be calculated with basic mathematics. Developing this perspective is a crucial part of systematic preparation, and strengthening it through practice in drills as well as GMAT mocks ensures that you can approach even visually presented probability questions calmly and solve them with confidence under exam pressure.

Areal probability is applied when the probability of an event is represented as the ratio of a specific area to a total area. In other words, areal probability is used when the likelihood of an event is based on areas rather than counts. It is defined as the ratio of the favorable area to the total area. The formula is simple:
Probability = Desired Area ÷ Total Area.
For instance, imagine a square dartboard with side 10 units. A smaller square of side 5 units lies inside it at the center. If a dart lands randomly on the board, the probability that it hits the smaller square is the ratio of their areas: 25 ÷ 100 = 1/4.
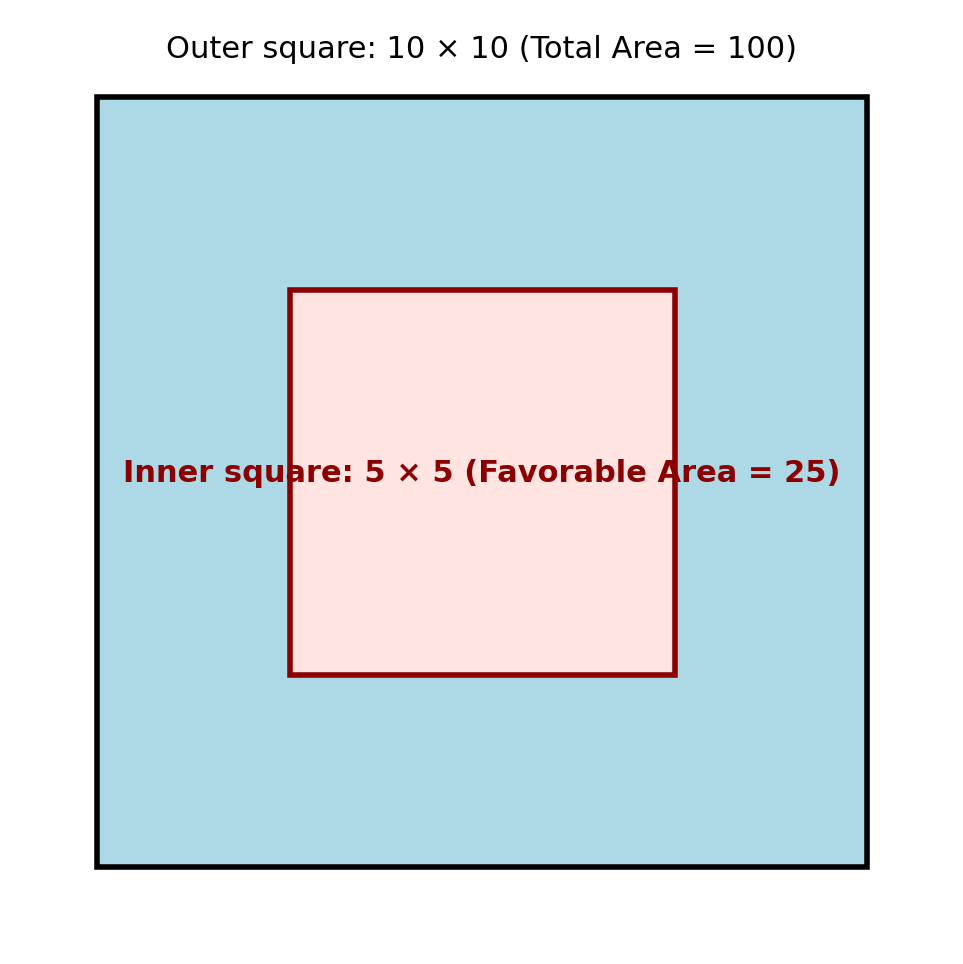
This simple idea underlies many GMAT geometry-based probability questions.
Question: Coordinates of two diagonally opposite points of a rectangle are (0,0) and (8,6). A point is randomly selected on the rectangle. What is the probability that the y coordinate of the point is greater than its x coordinate?

The rectangle extends from (0,0) to (8,6). This rectangle represents the total region.
We need the region where y > x. Drawing the line x = y, we see that the line intersects the rectangle at (6,6). The area above this line within the rectangle is the favourable region.
The total area of the rectangle = 8 × 6 = 48
The favourable area is the triangle with base 6 and height 6. Its area = ½ × 6 × 6 = 18
Probability = Desired Area ÷ Total Area
= 18 ÷ 48 = 3/8
Therefore, the required probability is 3/8.
Areal probability shows that visualization is as important as computation. By drawing the figure, identifying the condition, and focusing on the relevant region, the problem reduces to basic geometry. These problems are not about memorizing formulas but about training the eye to see boundaries clearly. Practicing such visualization as part of your GMAT preparation course develops both speed and accuracy, giving you confidence whenever a probability question takes a geometric form.
Life often unfolds like areal probability, where outcomes depend on the space we choose to focus on. In GMAT preparation, success comes from training the mind to filter distractions and see only the relevant region of thought, just as in visualizing the favorable area in a diagram. The B-school application process is also about defining boundaries: highlighting strengths, presenting experiences, and carefully shaping your story within the space available. In life, too, clarity of vision lets us recognize opportunities hidden in the larger canvas. The art of narrowing perspective is what converts uncertainty into confident action.