Equation of Circle on Coordinate Axes on GMAT

50 Word Summary

An equation of a circle represents all points a fixed distance from a center: (x − a)² + (y − b) ² = r², with center (a, b) and radius r. Example: for a circle with center (0, 0) and radius 3, the equation is x² + y² = 9.

Overview

Understanding the equation of a circle is a key part of coordinate geometry, and it often forms the basis for more complex problems. The general form of a circle’s equation is built around two simple elements: its center and its radius. Once you know these, you can express the circle in the standard mathematical form and use it to solve questions related to points lying inside, outside, or on the circle. This concept may sound basic for GMAT prep, but it regularly appears in test scenarios where students make avoidable mistakes by rushing through the setup. Master the concept and apply it in your GMAT drills and GMAT mocks for adequate practice. After each session, analyze your performance carefully, with special attention to incorrect attempts.

Equation of a Circle Explained

The equation of a circle provides a simple but powerful way to represent a circle on the coordinate plane. The standard form is:

(x − a)² + (y − b) ² = r²

Here, (a,b) represents the coordinates of the center of the circle, and r is the radius. This equation holds true for every point lying on the circumference of the circle.

Example 1: Circle with Center at (5, 7) and Radius 7

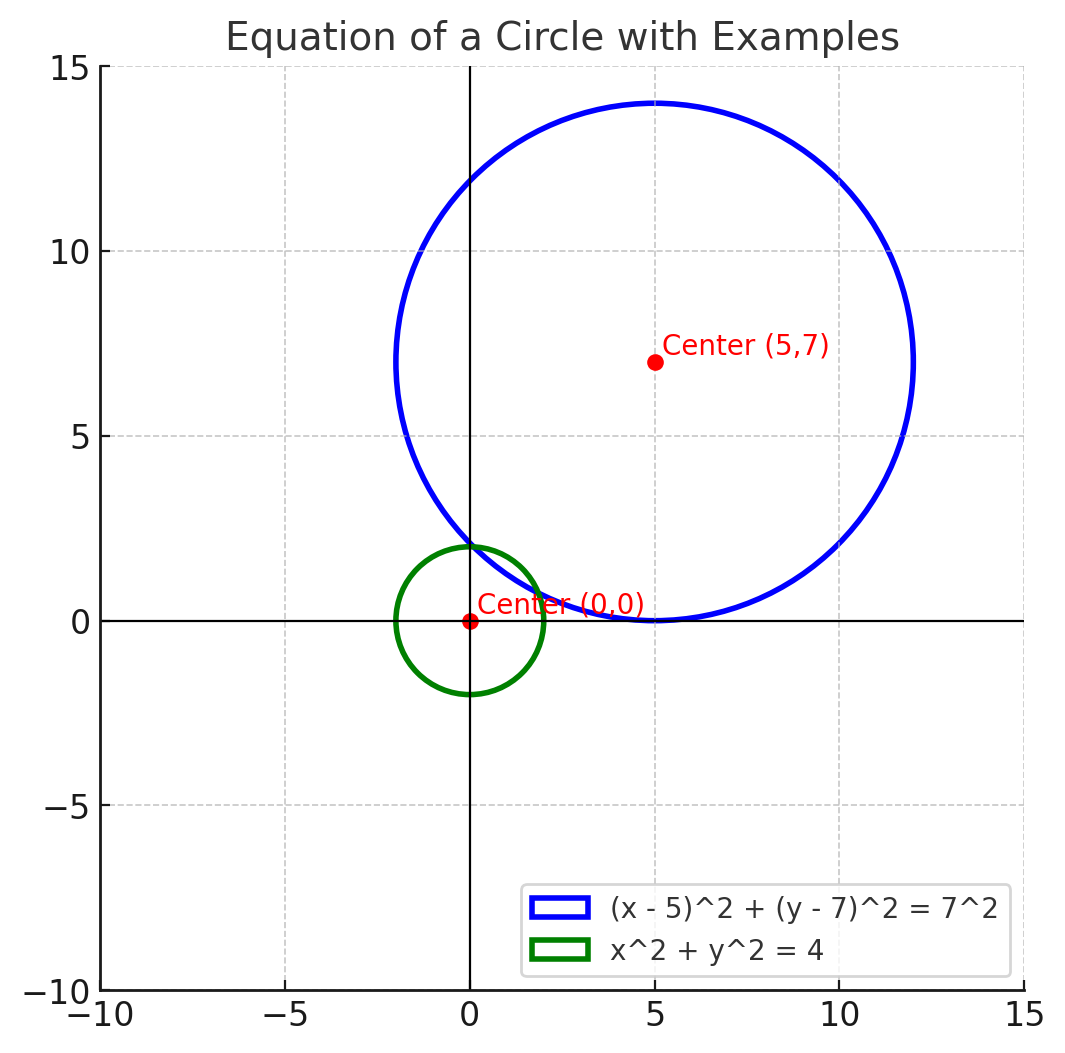
If the center of a circle is at (5,7) and its radius is 7, the equation becomes:
(x−5)² +(y−7)² = 7²
This equation captures all points that lie exactly 7 units away from the center of the circle, represented by the point (5,7).

Example 2: Circle with Center at the Origin and Radius 2

If the circle is centered at the origin (0,0)(0, 0)(0,0) and has a radius of 2, the equation is:
(x−0)² +(y−0)² = 2²
or simply,
x² + y² = 4

Wish to know your current GMAT level? Take a free, full-length GMAT mock

Parting Thought

Circles teach us to pick a center before we measure distance. In GMAT preparation, let mastery be your center and set a radius of daily practice you can sustain, then touch the circumference with steady milestones. In the MBA applications process, choose a purpose as your center, define boundaries of time and energy, and reach programs that lie on a realistic arc. In life, values choose the center, ambitions set the radius, and growth is the quiet journey from within to the edge. When the center is steady, every point aligns. When the radius expands patiently, new horizons become reachable!