Invest 30 seconds...
...for what may lead to a life altering association!
Help Line
- +91.8800.2828.00 (IND)
- 1030-1830 Hrs IST, Mon-Sat
- support@expertsglobal.com
...for what may lead to a life altering association!


Distance between two coordinates (x1, y1) and (x2, y2) is the straight line length between points, computed by √[(x2 – x1)2 + (y2 – y1)2]. Example: between (0, 0) and (3, 4), the distance is √[(4 – 0)2 + (3 – 0)2] = 5. Hence, the distance is 5 units.
In coordinate geometry, one of the most important skills is finding the distance between two points. This distance is not simply the difference in x or y values but the straight-line distance connecting them, also known as the Euclidean distance. The formula is derived from the Pythagoras theorem and provides a reliable way to measure separation between any two coordinates on the plane. For example, the distance between the points (2, 3) and (4, 6) comes out to √13, which represents the exact straight-line measure. A strong command of this concept is essential because such distance-based questions frequently appear in the exam. Building accuracy in topics like coordinate geometry not only sharpens problem-solving but also strengthens your preparation for more complex applications. For further structured guidance, explore our GMAT on-demand course for end-to-end concept building as well as rigorous practice.

The distance between two points in a coordinate plane can be calculated using a simple but powerful relationship. If the two points are (x₁, y₁) and (x₂, y₂), then the distance between them is given by:
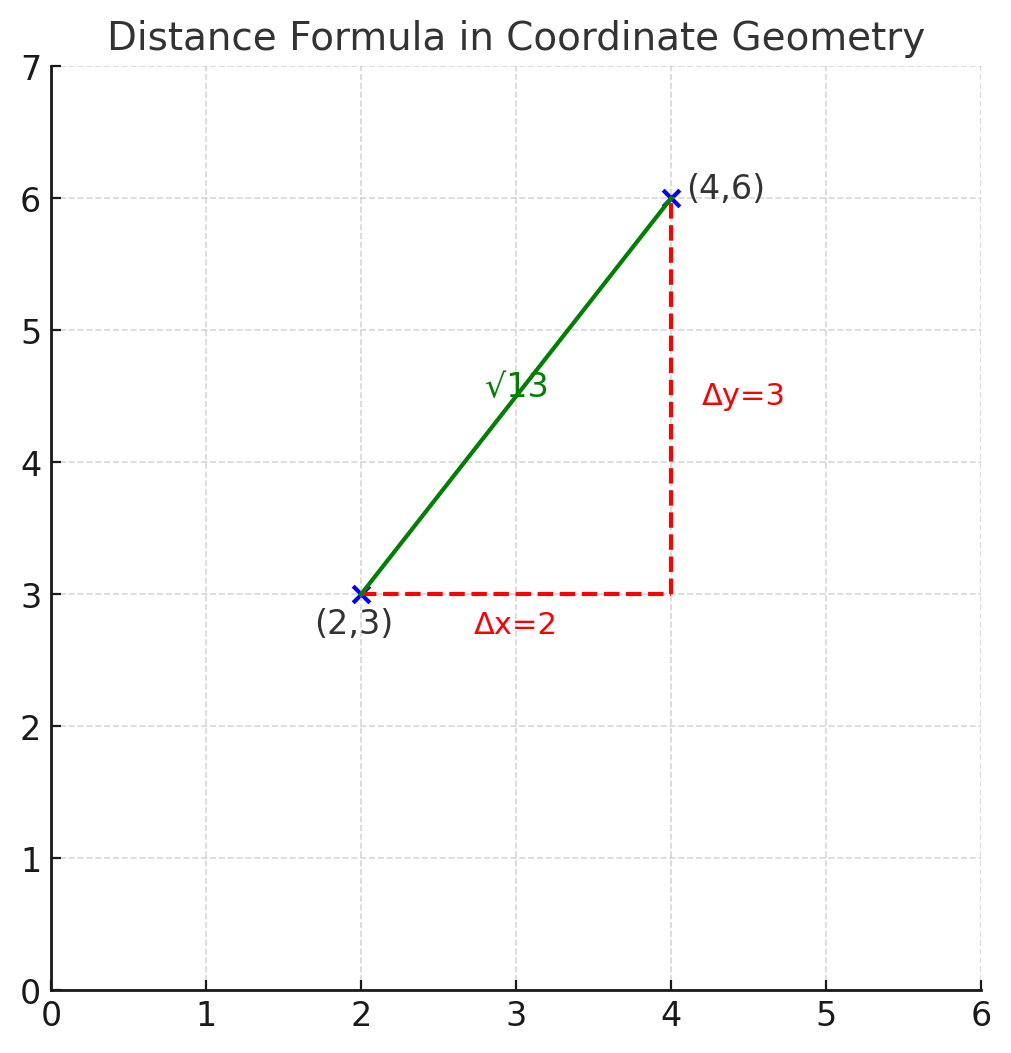
This formula comes directly from the Pythagoras theorem. Imagine a right triangle where the difference in x-values represents one leg, and the difference in y-values represents the other. The straight-line distance between the two points is then the hypotenuse of this triangle.
For instance, if the coordinates are (2, 3) and (4, 6), the difference in x-values is 2, and the difference in y-values is 3. Substituting into the formula gives √(2² + 3²) = √13.
Mastering this formula is vital for tackling coordinate geometry questions with speed and precision on GMAT drill as well as GMAT full length tests.
Distance teaches humility and method. Between two points, progress comes from resolving the horizontal and the vertical, then moving with intention. GMAT preparation works the same way: diagnose gaps in concepts and timing, plan the shortest straight line, and take steady steps. In the B-school application process, map the space between your present profile and your target program, align essays, recommenders, and deadlines, and close that gap with honest effort. In life, measure where you are, choose a clear direction, remove detours, and walk consistently. Small, correct moves add up, and the line from intention to result becomes shorter daily.