How to Find Equation of a Line on GMAT

50 Word Summary

An equation of a line represents every point (x, y) on a straight path. Common forms: slope-intercept form: y = mx + c; intercept form: x/a + y/b = 1; two-point form (x – x₁)/(x₂ – x₁) = (y – y₁)/(y₂ – y₁).

 

For rigorous practice on full-length mocks, explore our 15 GMAT mock tests!

 

Overview

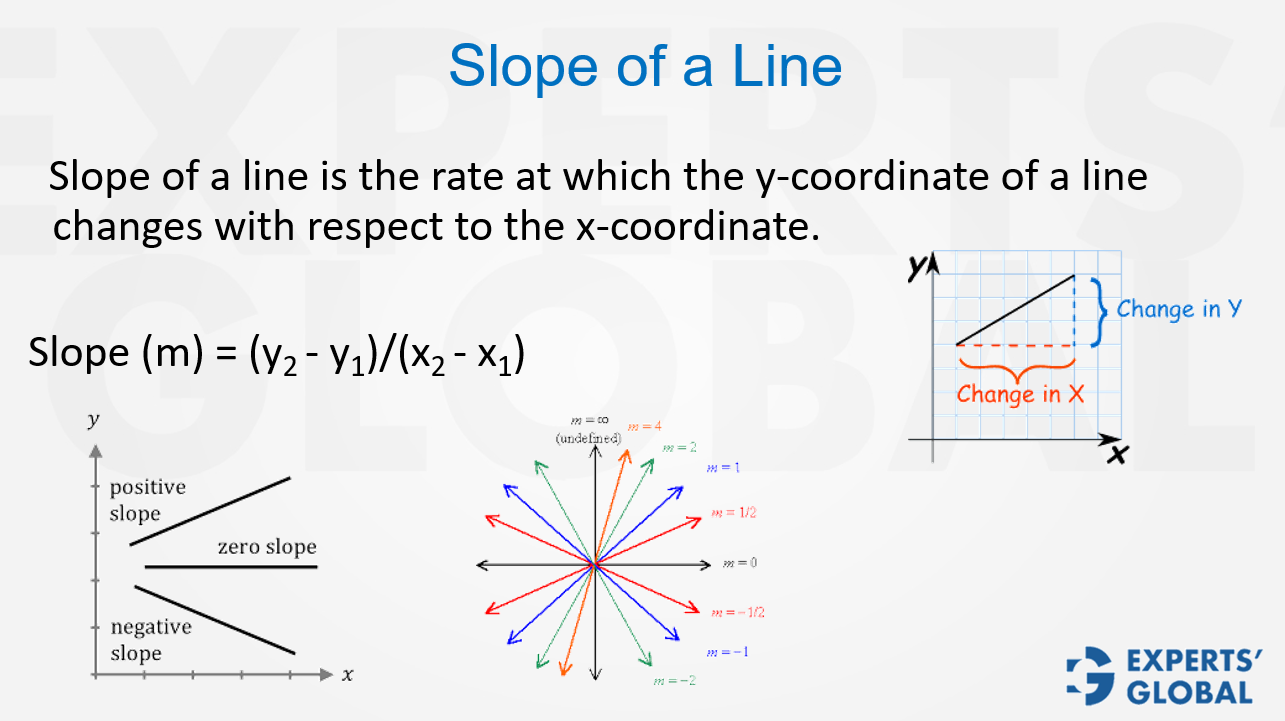
Understanding how to form the equation of a line is a vital skill in coordinate geometry and a concept that frequently supports problem solving during GMAT preparation. A line can be expressed in different forms depending on the information available, and being comfortable with these forms can help you quickly recognize patterns in questions. The most commonly used is the slope-intercept form, y = mx + c, where m represents the slope of the line and c represents the y-intercept. Another useful form is the intercept form, x/a + y/c = 1, where a is the x-intercept and c is the y-intercept, handy when you know the intercepts on both axes. Besides, when it is known that a line passes through two points (x₁ y₁) and ( x₂ y₂), the equation of the line can be determined using the two-point from: (x – x₁)/(x₂ – x₁) = (y – y₁)/(y₂ – y₁). Duly understand these relationships and apply these on your practice drills as well as GMAT simulation, for due practice.

 

Finding Equation of a Line on the Coordinate Axes (xy-plane) on GMAT

The equation of a straight line can be expressed in multiple ways depending on what information is given. The two most widely used forms are the slope-intercept form and the intercept form.

Slope-Intercept Form

 

The slope-intercept form is written as y = mx + c, where m denotes the slope of the line and c represents the y-intercept. The slope itself can be computed as (y₂ – y₁)/(x₂ – x₁) when two points on the line are known. This form is particularly useful when you know the slope and one point on the line, or when the y-intercept is already provided.

 

Intercept Form

Another representation is the intercept form: x/a + y/c = 1. Here, a is the x-intercept and c is the y-intercept. For example, if a line has x-intercept 2 and y-intercept 3, its equation can be written as x/2 + y/3 = 1, which is equivalent to 3x + 2y = 6.

 

Equation through Two Points

If the line passes through two known points, say (x₁, y₁) and (x₂, y₂), its equation can be found using the relation:

(x – x₁)/(x₂ – x₁) = (y – y₁)/(y₂ – y₁).

This is often called the two-point form and is one of the most practical ways to establish the line’s equation.

Parting Thought

Lines teach alignment. A line is defined by a slope and a point; progress is defined by direction and a starting place. In GMAT preparation, choose a steady slope of effort, anchor your plan at today’s point, and let daily practice trace a clear path. In the B-school application process, align values with goals, let your essays pass through honest coordinates, and keep recommenders on the same gradient. In life, decide the rise you want for each run of time, remove noise, and keep moving with clarity. When direction is chosen and maintained, outcomes follow the simplest linear rule predictably.

 

Targeting ISB? Check out our ISB admission consulting module!