Invest 30 seconds...
...for what may lead to a life altering association!
Help Line
- +91.8800.2828.00 (IND)
- 1030-1830 Hrs IST, Mon-Sat
- support@expertsglobal.com
...for what may lead to a life altering association!


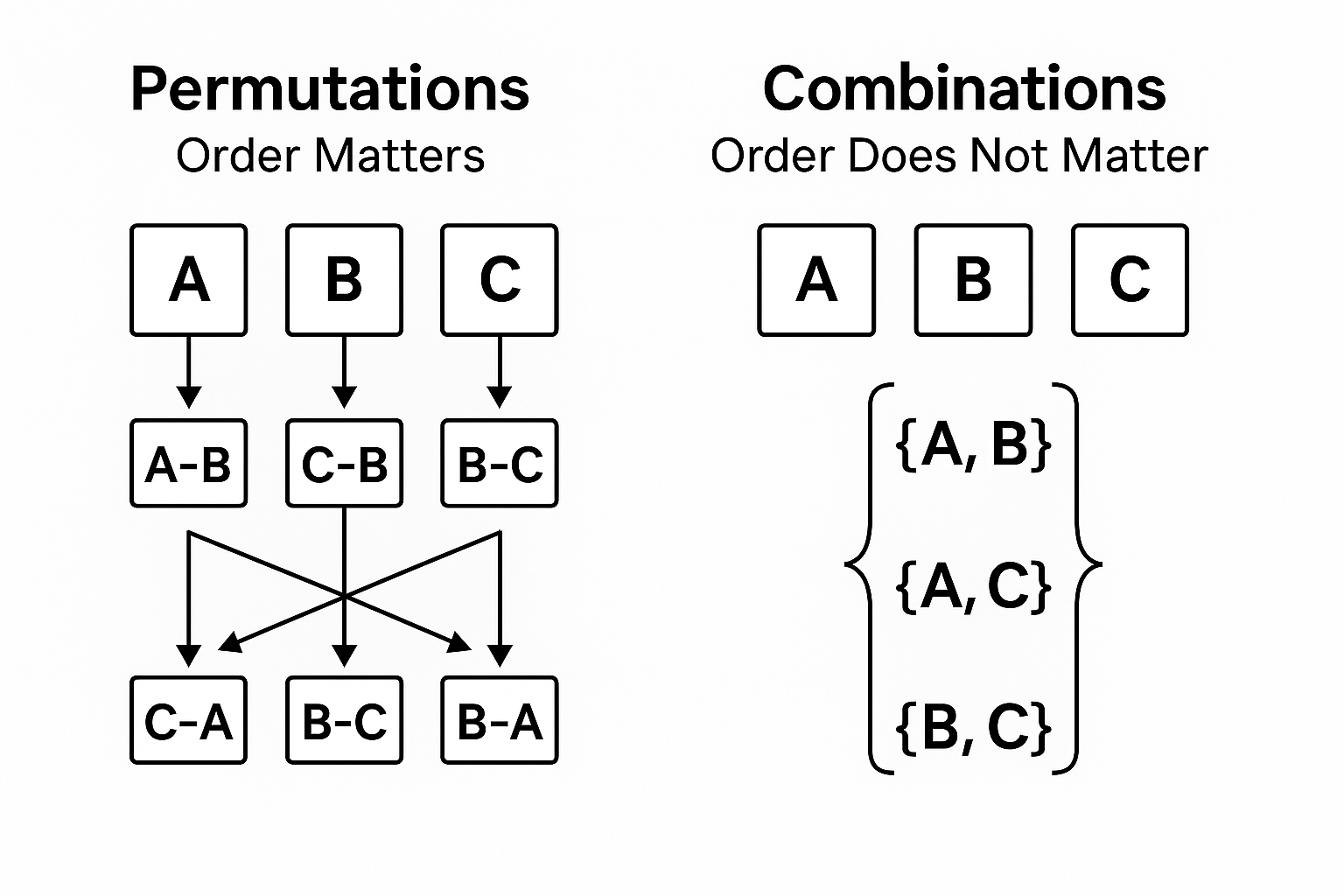
Permutations and combinations are counting methods. Permutations apply when order matters, such as arranging 2 books out of 4 on a shelf, giving 12 ways. Combinations apply when order does not matter, such as choosing 2 books from 4, giving 6 ways.
Is ISB your prime target? Check out our ISB admission consulting package
Many students confuse permutations and combinations, often using the wrong one in GMAT problems. The key difference lies in whether the order of arrangement matters. When the order is important, permutations must be used. When the order does not matter, combinations are applied. This simple distinction changes the entire approach to a problem, and overlooking it can lead to costly errors. For instance, arranging students in a line is a case of permutations because the sequence makes a difference. On the other hand, choosing a group of students for a project team is a case of combinations because the order of selection does not matter. Understanding this concept is essential to mastering GMAT Quantitative Reasoning, and practicing such cases helps build confidence. To sharpen your preparation further, consider opting for a conceptual GMAT prep course and strengthen your foundation in combinatorics.

Permutations and combinations may appear similar because both deal with counting possibilities, but the heart of the matter is whether the sequence of items makes a difference.
A permutation is used when the arrangement or sequence is important. For example, placing children in a row is a permutation problem. If child A and child B switch places, the result is treated as a new arrangement. Every possible sequence is counted separately, which is why the total number of permutations is usually larger than the number of combinations for the same scenario.
Combinations are applied when the order is irrelevant. If you are arranging identical chocolates, swapping one with another does not create a new arrangement. Similarly, choosing members for a team is a combination problem because the group remains the same regardless of the order in which members are picked.
The GMAT often tests this concept in subtle ways. Mistaking a combination for a permutation, or vice versa, can change the entire outcome. Always pause to ask: does order matter in this question? This single step can prevent errors and improve accuracy. Regular practice through GMAT mock tests along with due analysis will further sharpen your ability to spot the difference quickly.
In many ways, the difference between permutations and combinations mirrors the choices we face in GMAT preparation, business school applications, and life itself. Some decisions demand that we focus on order, sequence, and timing, much like permutations. Others require us to look only at the essence of the choice, as in combinations. Success lies in knowing which perspective to adopt at the right time. In GMAT study, clarity on this distinction leads to accuracy; in B-school admissions, it guides priorities; and in life, it teaches us to balance detail with perspective, action with reflection.