Set Theory: Two Overlapping Sets on GMAT | Venn Diagram

Quick Summary

Use a two-set Venn diagram correctly: write each set’s total outside its circle, place ‘neither’ outside both, and compute the overlap first. Then fill only-A and only-B. Check with overall headcount. Remember ‘A or B’ means A, B, or both, which is everything except neither.

Overview

Venn diagrams are one of the simplest yet most powerful tools to approach set-based problems on the GMAT. The key is to organize the information so that nothing is missed and every part of the set is represented clearly. When only two sets are involved, say A and B, the totals for each set should always be written outside the circles. The overlapping region becomes the most important element, since it represents the items that belong to both sets. The outer region represents those who belong to neither. Non-overlapping parts of the two circles represent ‘A but not B’ (or only A) and ‘B but not A’ (or only B) respectively. Once you set up this structure, you can answer every follow-up question with confidence. This technique ensures that you do not get lost in the wording of the problem and instead rely on a clean visual representation. Approaches like this, reinforced through an efficient GMAT preparation course and applied in GMAT practice tests, build the clarity and confidence required on test day

 

Understanding Two-Set Venn Diagrams

When dealing with two sets, such as A and B, the correct way to represent the data is to place the totals outside the circles. The overlap between the two sets represents those who belong to both. The outer region, outside the circles, represents those who belong to neither. Every part of the diagram has a clear meaning: only A, only B, both A and B, neither, and A or B.

 

Key Idea

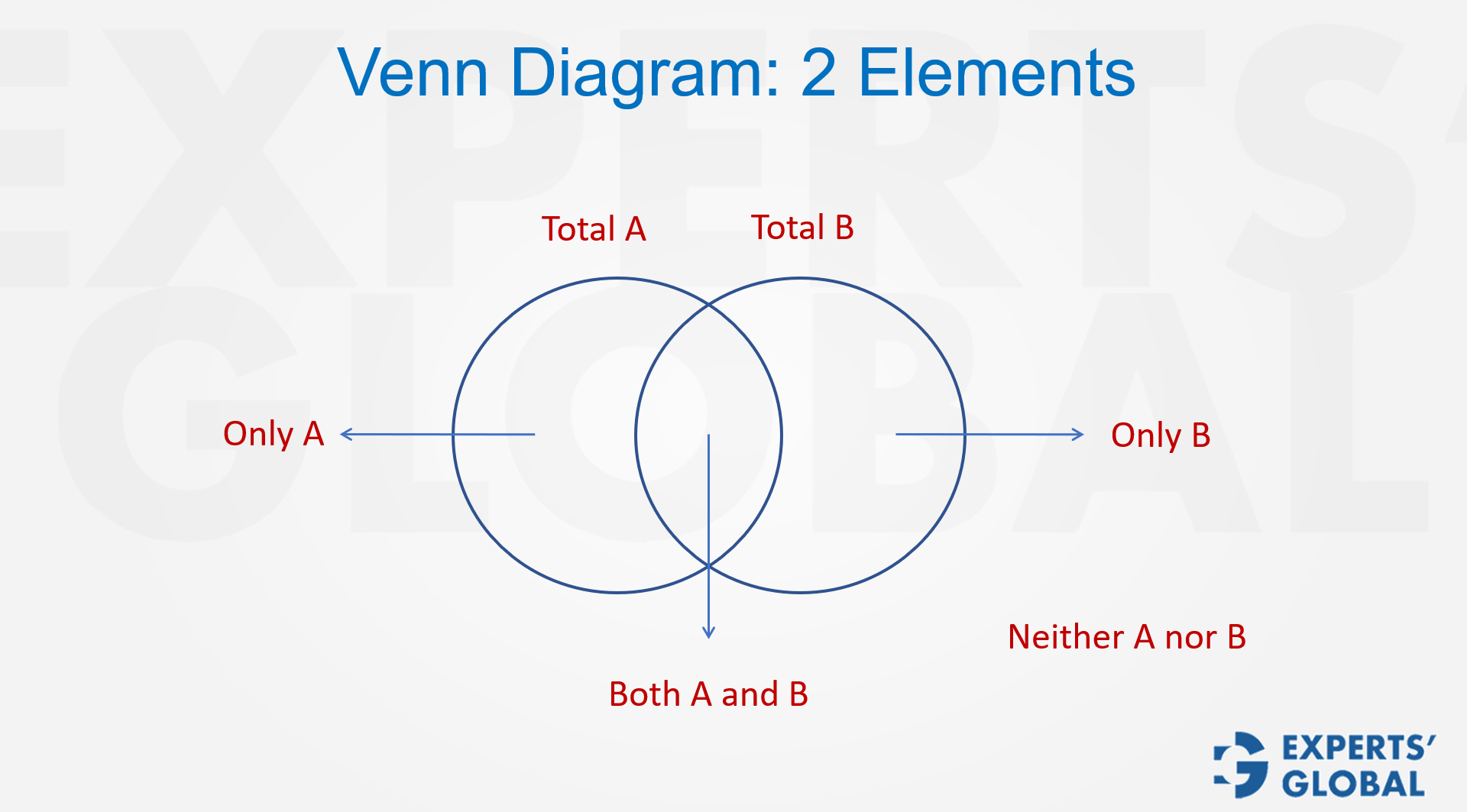
Write each set total outside its circle. Treat the overlapping region as the most important piece, because it controls the “only” regions and every follow-up count. “Neither” lives outside both circles. “A or B” means A, or B, or both, which is everything except “neither.”

An Explanatory Question

In a group of 120 people, 70 play Soccer, 100 play Cricket, and 10 play neither game.

1. How many play both Soccer and Cricket?

2. How many play exactly one of the two games?

3. How many play only Soccer?

4. How many play only Cricket?

5. How many play at least one of the two games?

 

Solve Step by Step

1. Draw two circles, Soccer and Cricket. Write totals outside: Soccer = 70, Cricket = 100. Note the headcount = 120 and “neither” = 10 outside both.

2. Compute the overlap. When you add the set totals and also count “neither,” you have overcounted by exactly the overlap.

    Overlap = Soccer total + Cricket total + Neither − Headcount

    Overlap = 70 + 100 + 10 − 120 = 60

3. Fill the diagram:

    Both = 60

    Only Soccer = 70 − 60 = 10

    Only Cricket = 100 − 60 = 40

4. Read any required count directly from the diagram:

    “At least one” = Headcount − Neither = 120 − 10 = 110

Answer Each Part

1. Both Soccer and Cricket: 60

2. Exactly one of the two: 10 + 40 = 50

3. Only Soccer: 10

4. Only Cricket: 40

5. At least one: 110

Why This Works

The outside totals fix the size of each circle. The headcount ensures every person is placed exactly once. The difference between what you “add up” and what you “actually have” is the overlap.

Common Mistakes to Avoid

• Forgetting to place “neither” outside both circles.
• Treating “A or B” as only one set, instead of A, or B, or both.
• Treating “A or B” as only one set, instead of A, or B, or both.
• Losing track of the headcount check.

A Final Word

Mastery grows when you draw with care, verify with the headcount, and answer gently from the diagram. If you are also planning your broader journey, our MBA admission consulting can help you align preparation timelines with applications, so your effort in class, on test day, and beyond tells one clear story.

Parting Thought

A two-set Venn diagram reminds us that clarity comes from structure. Just as overlap and separation together reveal the full picture, preparation for the GMAT calls for balance between precision and perspective. The discipline of organizing information strengthens not only problem-solving but also decision-making in MBA applications and later in life. Seeing how each effort belongs to one circle, the other, or both, teaches us to recognize connections across domains. Practicing such frameworks in GMAT simulation builds a habit of careful reasoning, reminding us that clarity grows when complexity is mapped with patience.